Amid enormous shifts and distortions in consumption and trillions of dollars handed out by the government and the Fed.
By Wolf Richter for WOLF STREET.
American consumers – those hundreds of millions of mythical creatures whose sole job is to consume more than they make – have paid down their credit cards again. In December, the crucial month for overspending with borrowed money, credit card balances and other revolving credit ticked down 0.3% from the prior month, to $976 billion, seasonally adjusted (green line in the chart below), according to the Federal Reserve Friday afternoon. This was down 10.8% year-over-year, the steepest year-over-year decline ever.
On a not seasonally adjusted basis (red line), credit card balances normally spike in December during the holiday shopping melee. But last December they didn’t spike nearly enough and fell 10.8% from the prior year, also the steepest year-over-year percentage drop, to $976 billion, a balance first reached in the good old days of September 2007.
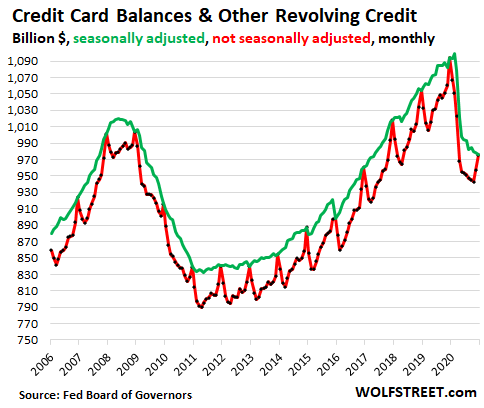
The seasonally adjusted balances are pegged to the not-seasonally adjusted December balances. That is why in the chart above, the green line (seasonally adjusted) is always way higher than the red line (not seasonally adjusted) except in December when they match. The idea of those big seasonal adjustments is to iron out the big seasonal volatility of credit-card usage.
The 10.8% year-over-year decline beat the prior record decline of October 2020 (-10.3%) and the prior steepest declines ever (-9.9%) in January and February 2010 during the Financial Crisis.
The $600 stimulus payments that started going out at the very end of December are likely not yet reflected in the data but will show up in the January data. And then there will be the next stimulus payments now being worked on in Congress. So the decline in credit card balances is likely not over yet:
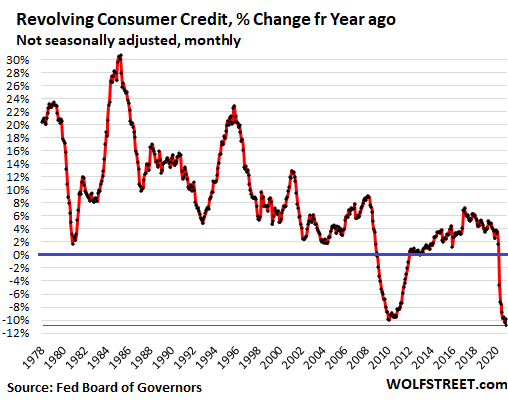
Until the Financial Crisis, there had never been a year-over-year decline in revolving credit balances. That was a new phenomenon, after decades during which Americans had amassed ever more credit card debt, buying things they couldn’t afford and paying breath-taking interest rates for the privilege. And so they did their job and consumed and cranked up the consumer economy.
That scheme blew up during the Financial Crisis, when masses of credit card borrowers defaulted and let banks eat the losses, along with the losses from their defaulted mortgages.
Now we have the second period of year-over-year declines, and it’s the steepest ever, but it’s not caused by defaults, but on one hand by huge amounts of government stimulus money in various forms, and on the other hand, by limits to consumption: Many services – restaurants, bars, sports venues, concerts, hotels, cruises, flights to exotic destinations, etc. – have become partially or totally unavailable.
Some of this money that would have been spent on these services was spent on goods, and the amounts of money spent on durable goods in 2020 spiked to records:
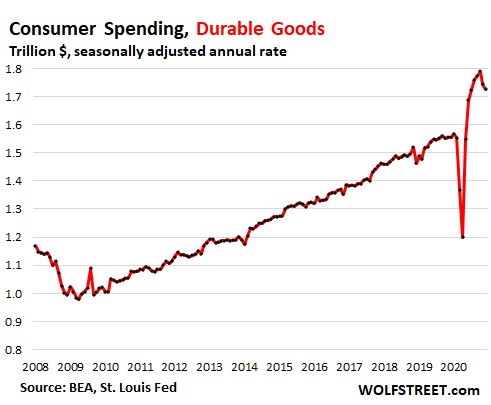
And some of the money that would have been spent on services and would have been added to credit card balances, was saved and a portion of these savings were used to pay down credit card debt. This has all become part of the Weirdest Economy Ever.
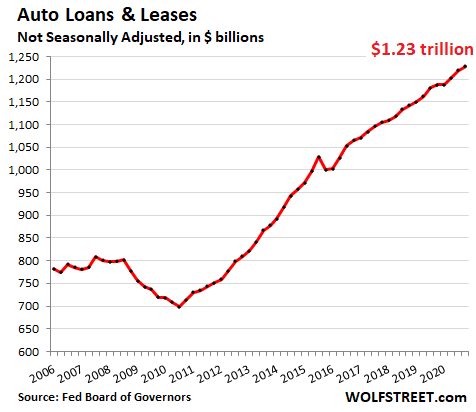
Auto loans.
The thing that happened with driving-obsessed Americans in 2020 was a 15% plunge in new vehicle sales, in terms of the number of vehicles sold: Only 14.46 million new vehicles were sold (red column) which took sales back to where they’d been in the 1970s:
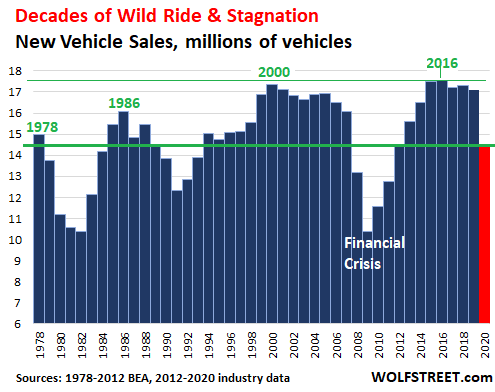
And used vehicle retail sales fell 6.25% in 2020, to 19.5 million vehicles, according to estimates by Cox Automotive.
But even as total new and used vehicle volume dropped sharply in 2020, prices spiked by 15% year-over-year in used vehicles during the summer and fall. And consumers with money – the beneficiaries of working from home and the Fed’s money printing – shifted to more expensive new vehicles, particularly trucks. All combined, they bought fewer new and used vehicles, but they paid a lot more for them, and they therefore financed (including leasing) more in aggregate.
So balances of auto loans and leases – despite the decline in unit sales – rose to a record of $1.23 trillion at the end of 2020, up 3.5% from a year earlier:
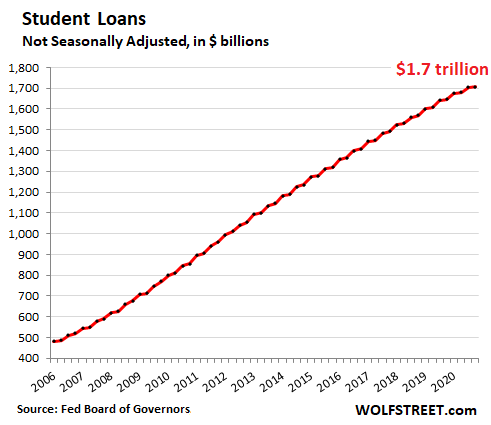
Student loans.
The thing that happened with student loans in 2020 is automatic forbearance for federal student loans, the vast majority of student loans. No one has to make payments on those loans. Forbearance has been extended through September 2021. So the normal loan principal payments, which had already slowed to a trickle in prior years due to the many deferral programs, further slowed.
And new student borrowing was added to the top of this pile, which in Q4 grew by 3.7% from a year ago to a record $1.7 trillion, not seasonally adjusted, according to the Federal Reserve Friday afternoon. Nevertheless, it was the smallest year-over-year growth in the data going back to 2006, likely due to drastically reduced spending on room and board as many colleges and universities switched to remote classes, with many students living at home:
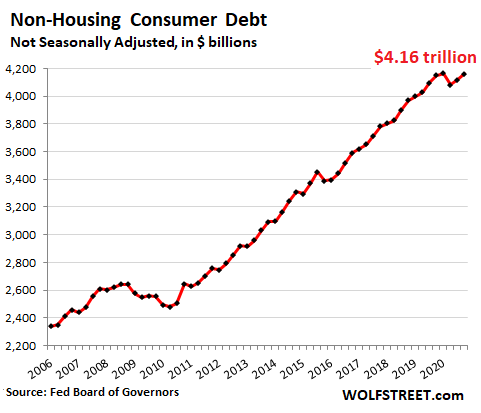
Total non-housing consumer debt.
Given the year-over-year plunge of credit card balances and the increase in auto loans and student loans – but not including housing-related debts, such as mortgages and HELOCs – total consumer credit at the end of 2020 edged up 0.2% from a year earlier, to $4.16 trillion, but was a hair below the record of Q1 2020:
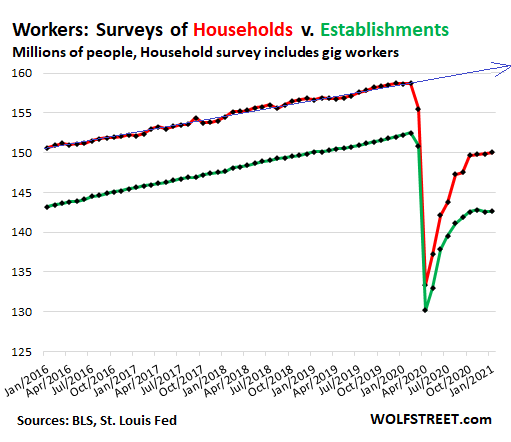
And this borrowing — or failure to borrow enough, as it were — is taking place in an economy with enormous shifts and distortions amid trillions of dollars handed out by the government and the Fed, where some people have hugely benefited, and others have gotten crushed, as at least 10 million more people are still unemployed than were a year ago:
Enjoy reading WOLF STREET and want to support it? You can donate. I appreciate it immensely. Click on the mug to find out how:
![]()


So, basically people are paying off their credit card debt to buy trucks. And probably houses. Since price inflation for both of those items has been enormous, debt slaves have had to reduce credit card balances to get their credit ratings up so they could get truck and house loans.
Is that what’s happening?
Some people are probably skipping mortgage and rent.
Very large arrears on rents. I have seen reports at about the $80 billion level.
They’re stiffing the landlord and buying new vehicles in record numbers. This stiffing the landlord and the bank thing is the reason for all of this spending. It’s despicable.
To a certain extent, bankruptcies force a degree of accounting, a tracing of assets.
And creditors can initiate bankruptcy (although that is the surprisingly more rare avenue…debtors, even individual debtors, are usually the ones filing).
So it will be interesting to see how this all plays out.
My guess is that the G, using some of the vast sums of printed money, will at
make the landlords at least partially whole.
But I can also see the G leaving the landlords to hold some of the bag.
So, then, a wave of landlords filing bankruptcy actions against tenants deeply in rent arrears, but with new cars (with much equity?)?
Who knows.
I really don’t know what our politicians were thinking. On one hand, give people printed money to stay at home, and at the same time, tell them there are no real consequences for not paying their rent.
What exactly did they think was going to happen?
Right. When politicians decided to give “an extra $600 per week,” they should not have also allowed stiffing the landlord and the bank. It should have been EITHER/OR. You either do “an extra $600,” OR enact rent and mortgage moratoriums. I hate all of these people – the politicians and the freeloaders.
Depth, this is ultimately the problem with universal franchise.
““A democracy cannot exist as a permanent form of government. It can only exist until the voters discover that they can vote themselves largesse from the public treasury. From that moment on, the majority always votes for the candidates promising the most benefits from the public treasury with the result that a democracy always collapses over loose fiscal policy, always followed by a dictatorship. The average age of the world’s greatest civilizations has been 200 years. These nations have progressed through this sequence: From bondage to spiritual faith; From spiritual faith to great courage; From courage to liberty; From liberty to abundance; From abundance to selfishness; From selfishness to apathy; From apathy to dependence; From dependence back into bondage.”
– Alexander Tytler
Old Engineer,
I wonder how the total debt picture looks when mortgage debt is thrown in with the consumer debt, and then another chart shows consumer debt + mortgage debt + all US government debt + all other debt like margin debt? My guess is that the US American nation as a whole is still on a debt binge and QE will continue to accelerate until it can’t.
I think the total financial paper to gdp is about 6 X gdp. Total debt is around 3.5 – 4.0 GDP. It’s impossible to know how it’s going to play out for sure but normally the paper bubble will burst and the 6 X paper assets would become 3 X or 4 X but all the talk coming out of DC is we have to let the debt bubble keep going.
There is a lot of bad debt that will never be paid. Some examples are a lot of student debt, lower quality corporate debt and government debt. It will be honestly written off or will be inflated away. It’s hard to know how it’s going to play out. You either have to diversify to play both scenarios or stayed glued to financial information each and every day to be first one in the life boat.
“and the 6 X paper assets would become 3 X or 4 X ”
“There is a lot of bad debt that will never be paid”
That is the dynamic that is vastly underdiscussed.
The illusion of normalcy from 2002 to 2019 was purchased by having ZIRP starved savers finance horribly underwritten, doomed loans to tens of millions, so that home/auto/etc purchase volumes could be propped up (at prices impossible to sustain absent that vast, doomed financing).
When you receive a stimulus check the debt shifts from private to public. Private debt equals public good, and public debt crowds out private (business) spending. That last part doesn’t really work, since QE accompanies an expansion of corporate debt, unless we assume that the Feds disincarnate borrowing isn’t debt at all but an expansion of the money supply, and those stimulus checks are just the extra dollars. Therefore the whole process is debt neutral, which may explain the anemic recovery.
AB,
I am getting parts of that, but I think stepping through it/restating it in a bit more incremental detail might help.
The thing about macro manipulation of the economy is that it tends to work in ways alien to the conception of those of us who spend our days surviving under micro constraints.
The G doesn’t consider itself particularly bound by micro rules (ahem, law, Constitutionality, etc., when it comes to macro finance) so the implications of macro actions can be seemingly odd.
And, in practice, unpredictable too.
And, not infrequently, bad.
I predict that the “Federal” Reserve’s QE will continue to accelerate “to infinity and beyond!” Unfortunately, that means most Americans will not profit from paying down their debts in an ultimately, inflationary economic situation.
I think that I was wrong in comparing what will happen to the events during the Weimar Republic. It will actually be more like Zimbabwe in 1992: except to the extent that foreign governments or investors decide to help stem it, hyperinflation will inevitably start because the “Federal” Reserve will keep printing dollars to help its banksters in sums far in excess of the spending of the government, which itself will be massive but insufficient to prevent all the foreseeable mortgage defaults, evictions, business closures, etc. See Nasdaq.com’s ”
Fed’s Powell: “Not the time” to discuss any change to bond purchases.”
The death/contraction of US businesses due to the pandemic will mean that, as in Zimbabwe when the farms of the white farmers were taken away and given to persons who were not able to run them, so the goods produced by that country decreased but the money printing accelerated, there will be more and more US dollars chasing fewer and fewer US goods. (Foreign governments/investors reportedly are not increasing their US treasury holdings significantly, so its all “Fed,” baby. See “A $1.8 Trillion Bond Glut Imperils Treasuries’ Seven-Year Rally” in Bloomberg.) This is similar to what happened in Yugoslavia during its economic disaster right before its break up.
Thus, the “Federal” Reserve will need to print out many, many TRILLIONS of dollars more than the US government’s huge needs just to bail out the banks, who own the shares of its “Federal” Reserve district banks. The “Federal” Reserve’s website lists the current real estate debts of banks at $4.64 TRILLION, MBS of $2.597 TRILLION in line 3, and lists “loans and leases in bank credit” at over $10 TRILLION, aside from $2.5 TRILLION in commercial loans. See the federalreserve.gov’s “H8. ASSETS AND LIABILITIES OF COMMERCIAL BANKS IN THE UNITED STATES” in page 3, lines 3 and 9 to 11 of the schedule of the banks’ assets for January 2021.
The banks were already in trouble in 2019 or their “Fed” would not have had to help them in the repo market nor have had to create $2 TRILLION just to buy that much of their mortgage-backed securities at over-valued prices in 2019 to 2020. The ongoing, increasing defaults in residential mortgages, defaults/arrearages in residential rents, and the defaults/arrearages of commercial tenants and consequent inability of both residential AND commercial landlords to repay those debts mean that major banks are now over their heads in the guano.
Many or most commercial loans will also likely default. The banks’ dividends and other compensation payments to executives and shareholders (e.g., by share buybacks in the tens of billions in 2019) decreased their liquidity so much that as of today they may not just be legally insolvent because they almost certainly have less in realizable, marketable, total assets than their liabilities that they owe but because they may even be unable to even meet their current obligations without their “Fed” printing US dollars to gift to them.
The administration just announced that this pandemic will not be resolved before the end of the summer and recent, scientific reports are alarming. Thus, nothing will get better for a while.
Does anyone really doubt that their “Fed” will keep the QE going “to infinity and beyond,” which incidentally gives the banks huge commissions for enabling the QE, aside from providing “dividend” funds and ultra low-interest loans to those banks? They also need to bail out their cronies’ companies and crony-foreign banks.
To keep the stock market booming for their bankster-cronies, they will also need to manipulate the stock market as the common sense intermittently starts returning to investors. Like drunks kept drunk by a crooked bartender, investors will have to see their stocks kept up with QE infusions or eventually, they will bolt and the stock market will crash. The “Fed” does not mind.
After all, it is not their money. It is just the legal tender for which millions of Americans toil long hours for all their miserable lives: as they think of them, the little (unimportant) people. Printing more and more US dollars to give to the banksters only amounts to more thefts from the savings, pensions, goods, and wages of the docile, little people.
They do not matter. Hence, here comes hyperinflation like in Zimbabwe, sooner or later.
There will also be a fight to prevent/reduce aid to the little people, because the banksters will not like to share the fruits of their “Fed’s” money printing with the little people. (Of course, that money would have reduced or delayed the mortgage and rent defaults, but they do not consider that.) The resulting, insufficient, minimal aid to the little people will only increase and accelerate the inevitable rent defaults, mortgage arrearages, business collapses (since consumers without money will not spend it), declines in sales, etc.
Zimbabwe, we are about to follow your disastrous example!
This economic situation is so vastly and completely different than what happened in Zimbabwe that I have a hard time taking your comment seriously.
I don’t think your predictions are going to age well, let’s put it that way.
History doesn’t always repeat. New things happen. The search for historical analogues to our present situation is in my view, totally in vain.
No, people with credit card debts cannot afford to buy cars and houses.
People buying cars and houses is the same kind of people that was doing it before only they are doing it less. But for cars it doesn’t matter because the prices have gotten highter and for houses it doesn’t matter because prices may go down in some cities but rise in others as a resultnof how much land with houses the USA has. So the only way for the housing market ti completely crash is if the economy does as that affects everyone and so that means a lot less house sales.
There’s plenty of people with credit card debts buying houses. Paying off a credit card is unlikely for many to be the difference between buying and not buying a house.
There could be some people who would pay off a credit card and then buy a car, but, I would guess it would be a used car most of the time.
The determimer of housing prices for most places comes down to whats the maximum loan the jobs in the area can support getting.
If the work from home trend becomes permanent for many though, the local job market could become alot less important for many areas, though as I think many of these workers will be laid-off and or replaced with cheaper workers, this trend will be hard to predict.
Many places in Florida for instance alternatively, comes down to attracting retirees, which has different factors for housing prices. Mainly how much money they have saved up and in investments at the time of house purchase and are unaffected by the local job market.
Credit card rates: 30% APR or some such.
Trucks and houses loan rates: between 1 and 2 %.
That’s your answer.
There’s a great scam going on in the auto industry where even the best credit only nets you a 4% rate oftentimes if you finance through the dealer’s preferred lenders. And, that’s the only way you get the best car deal. If you bring your own financing, the price goes up. You’re paying one way or the other. And if you pay cash the price goes even higher.
“If you bring your own financing, the price goes up.”
It has been a very, very long time since I bought a car.
Can others confirm this?
It wouldn’t shock me (knowing the games that can be played by shifting elements of total cost) but I would think the blatant-ness of it would spark consumer uproar/political hay.
There is nothing that stops people from going with the work-flow, take the dealer financing and then dumping excess cash into it or paying it off.
Except, the dealer financing has an option built into it: The loan is cleared simply by having the dealer repossess the car. There are some fees that goes with that option. If one believes that nothing will happen to ones income and the car will keep its value, then one could swap the dealer financing to a bank loan – which is likely cheaper in return for being full recourse.
If one has bought a shitty “luxury” car running on brand fumes, like Land Rover or the rust bucket Mercedes, then the dealer financing can be the only way to get rid of the thing “cleanly”.
I.M.O. There is no scam, just another service that of course has to be paid for. The dealers compensated for the risk of getting stuck with shitty, unsalable cars when their customers hit on hard times (or realised their car is actually shit and everyone knows, and therefore it has no value in the market).
Been there done that, several times last couple decades:
Ya just have to be prepared to stand up and walk away when the dealer folks start trying to pull that kind of stuff.
It was $250 delta for either cash or my bank vs dealer/mfr finance back in the 2007-9 era, so we went ahead with the dealers twice back then who were very upfront about it. Last deal was a bit over 50% off MSRP, so just handed them the CC (with the best cash back deal at the time.)
Last time, in 19, when the ”finance” guy pulled it, I left, and the GM or SM called me within the hour to confirm the original agreed pricing from when I ordered exactly what I wanted, and when I did not agree immediately offered me another 10% off.
At this point, thanks to thrift and sweat equity and thus no debt at all and the offspring on their capable own, it’s kinda fun to play this game,,, and the outcome just a few bottles of good ”liquidity” anyway, of which there appears to be a good supply.
Bottom line, ya just gotta be ready, willing, and able to walk away…
@Cas127: That’s how it works. The lowest price in my experience always comes with the requirement for dealer financing.
The play (not bragging, but we did it) is to take the dealer financing to get the lowest “price,” then call your bank and refi the loan for way way lower rates.
“Running on Brand Fumes”…..Good one!….. seems like lots of manufacturers are constantly seeking to improve that particular type of “efficiency”….Range Rovers can go anywhere.
Saw a big shot from Oracle with loaded “off road” Lexus SUV stuck in mud (winched out by tow truck) up in off grid hills…was muttering to much younger trophy wife, “But I had it in 4 wheel low”.
Conniving trophy wife, she dumped him for a her age musician type and they kept/lived in off grid house she had insisted they buy for weekends in the country.
Are the reductions in credit card debt due to paydowns by cash, Equity lines or credit or just another financing option like Lending Club?
Revolving credit, like Lending Club and payday loans, are included in the data, but they’re relatively small compared to credit card debts. A different data set by the New York Fed, which will come out in a few weeks, splits them out (quarterly only).
Lending club has about $60 billion in total credit outstanding. But this includes auto loans, business loans, and other loans. Only part of it is “revolving credit” for consumers.
“The $600 stimulus payments that started going out at the very end of December are likely not yet reflected in the data but will show up in the January data.”
I’m very curious to see these charts look like in a month or so. And after the next trillion dollar ‘stimulus’ works its way through the anaconda.
Making history, I tell ya…
$1.8 trillion.
A trillion here, a trillion there, pretty soon you are talking real money.
I’m old enough to remember when the saying was billions…taught to me by teachers who learned it as millions.
We live in a 000 society.
It’s much easier to deal with government numbers with exponential notation. $1.8 (now sometimes 1.9) trillion is only $1.8×10^12. That’s right, 12 zeros. These numbers no longer display in working people’s calculators.
Paradox:
New car dealer [GMC] is getting +10% over [window] sticker.
Exp. ’21 Canyon 4×4 crewcab w/diesel engine sticker was 43k. Two of them sold the day they came for 47k.
Addendum: a high end (gm/jeep) salvage facility noted how intense salvage auction bidding has raised the acquisition costs of wrecked cars.
Which has elevated used parts prices.
Owner expressed frustration from by being beaten out by competing facilities. It’s pay up or have limited sales from lack of components on the floor.
So in summary:
10 million more unemployed than a year ago,
Auto loans and leases still going up at record levels,
Student debt still going up at record levels,
Non housing debt still going up, after a brief shallow dip, at record levels,
Stock market at record levels,
Housing market at record level.
Pure madness and insanity, at record levels.
2banana,
Your last line nails it :-]
So, if 2banana is correct, then what is coming down, to compensate for the ‘record’ levels? Surely, madness and insanity are not a measurable value?
Why? Is it too insane to quantify insanity? I assure you the insane don’t give shit about your rationality, they’ll do as they please.
You have go to wonder how this will all end up during the good/normal times. Can the euphoria continue indefinitely? What could cause a stop in this movie like setup
Recently I was reading the Immigration policy of the Philippines. First written in 1940 I assume it has been updated over the decades. At the very bottom of the Immigration policy it gave a list of people who COULD NOT enter the Philippines. At the top of the list was “Idiots and lunatics are not permitted to enter the Philippines”. I kid you not.
A 1% hike in interest rates, if the Fed would ever allow it.
Happened from 2017 to fall 2018, then stock mkt fell by 20% by end of 2018.
Of course, “panic” set in and rate hike was reversed.
Even a tiny smidge of adulthood (even a purely head-fake taper) would end the asset inflation madness.
But all the Fed can see are those 10 million unemployed and the low employed to Population ratio.
And the fact that they only have money printing/int rate control as tools.
Nothing has changed from 2002 to now.. .that is how you get people physically scaling the wall at the Capitol (ie, Trump was much more a symptom than a cause).
People need to embrace the crazy and the madness, then everything else will seem rational.
Everything is in context… if there is anything I learned from reading this blog, it’s that it isn’t just one man who can keep crazy going, sure, it might take one guy to get crazy kicked off. But it takes a whole village to make sure crazy goes on and on and on… and it’ll keep going long after the initial loon who kicked off the party has been ejected. Heck, sometime, their name might not even be remembered very well any more… for example Gavrilo Princip
In football parlances, we’re not even half way through the first quarter at this point. There is a whole lot of madness and insanity left to go.
The reason for the crazy times will reveal itself soon. My guess it has to do with energy and peak oil.
It’s a new world!
The more I read, the more I’m convinced we’re in the middle to late stages of a crack-up boom.
That’s my sense, looking out for the blow-off top. Not sure what stage though ?
Crack up boom/blow off top…
Driven by drowning criminals dragging any one/every one down with them, who have foolishly tried to “help”.
this for cas10:
That’s EXACTLY the problem Cas,,, the really and truly criminals,,, the cronies and enablers of all this kind of shitstorm for WE the PEEDONs (thanks Unamused), do not have any kind of skin in this game/dog in this fight.
As has been mentioned many times on this site, the folks responsible for the irrational and criminal theft from working folks who have continue to save for their old age and now get nothing or so close to make no difference on their savings, etc., those folks, including the politicians and the employees of Fed, etc., etc., have inflation proof retirement at OUR EXPENSE,,, and no risk at all.
Even old folks are now beginning to be convinced about the ”light pole” remedy,,, and I can only hope The Great Spirits continue to watch over drunks and fools, since I apparently qualify on both counts…
Right,
I agree. I would also urge people, and always confirm with my kids, to look after personal fundamentals. Years ago my daughter and son in law rolled their student loans into a refi, then made a conscious decision to stay off the ‘trading up’ bandwagon. Their house will be paid for by age 50. Son not so prudent, (younger by 4 years) but now ‘getting it’ as he has purchased rentals that pay for themselves.
If people ever experienced the relief of retiring debt, I believe they would never drink from the poisoned well, ever again.
I have noticed for the past 20 years that many younger folks start out with all the goodies, or expect they should have them. Nice car, all the counter top appliances, etc etc. It all adds up. I’ve seen young couples buying houses in their twenties people would have bought at the height of their careers, and think it is is totally normal. Then, the marriage collapsed. At the very least they are looking at a lifetime of debt. It is a very hollow and sad value system, buying stuff for meaning and affirmation.
regards
ZIRP maximizes this pathological “now-ism” by,
1) Making exploited fools out of cautious savers and
2) Creating the illusion of affordability in overpriced consumer goods, as the all important “monthly cost” is kept artificially low.
After two decades, these dynamics are as close to religious principles as the US gvt gets.
Arguably employed to increase domestic employment but by now so ingrained into macro economic assumptions, that their removal has essentially become inconceivable, so fearful is the prospect.
Paulo, I recall a conversation with my Dad in the darkness of the expensive 70s’ when he said “The kids expect to have all the things their parents spent 20-25 years acquiring, and they want it all right now.”
Lisa, please re-read Paulo’s last sentence..SEVERAL TIMES!…although I doubt it will sink in, you are too far gone.
“The more I read, the more I’m convinced we’re in the middle to late stages of a crack-up boom.”
So that means stand up comedy is coming back?
Only if we laugh at the doom and gloom
“Pure madness and insanity, at record levels”.
Whatever you call it, it is accepted as the new normal and expected state of affairs.
New normal is driving those of us who value logic, reason, truth, and right conduct to question our own assumptions.
Are we crazy or are the others crazy? That is the question.
Heinz-perhaps “…logic, reason truth, and right…” should now be examined through a different lens, i.e. akin to that of a sickle-cell anemia that provides the body an added defense against malaria, but, by its own nature, does in its host later (‘cytokine storm’, anyone???).
(not that i disgree with you, just considering that ‘crazy’ could be a null term at present…).
may we all find a better day.
“Logic, truth, reason, right conduct……crazy….
https://pubmed.ncbi.nlm.nih.gov/31392845/
and “a different lense”.
It is always like this…always a “permanent high plateau” of idiocy, and then reality gets reintroduced.
In 2006/2007 “everyone” “had” to buy a house “immediately” because prices could/would “never” come down, ever.
It was just common sense and anyone who disagreed was just too stupid to understand the “new dynamics”
“It’s different this time.” I’m constantly hearing this. Meanwhile, I see massive bubbles everywhere I turn, that make the last bubble look mild by comparison.
I am trying to wrap my head around the housing increases of 15% in Evanston, I’ll up from one year ago. Who knows what’s happening with that. But the price increase means more down payment, and less cash reserves. I would at least hope this boom will level out and not continue to enter the stratosphere like it has in the Bay Area and NYC.
“Who knows what’s happening with that.”
Well, obviously the knowledge of how to build large wooden boxes has been lost for all time, so another new home can never be built…fixing the supply, driving up the costs of existing homes.
I mean, obviously….
The govt has it figured it out. Give’em $1,400, they’ll use it for a down payment on an overpriced vehicle or house.
Got to juice these prices a little higher.
And then what?
Well, even with a 5% down pmt, $1400 only gets you a $28k house, which would be a Port-a-Potty in NY or CA.
But you could get a $14k car priced at $28k.
Much like equity investors price in future inflation, borrowers are (I suspect) anticipating the Great Reset will include debt forgiveness for larger ticket items (autos, homes, student debt etc), so shedding smaller balances of high interest debt in the meantime makes sense. Maximize your benefit from the Great Reset ?
How would this debt forgiveness take place? Someone’s liability is someone’s asset.
MB
Politicians legislate based upon voter sentiment. Banks can be granted unlimited capital in our current system. Forgive debt, gift assets to debtors, then print more for lending.
If you an unlucky private creditor who cannot eat at the printing trough, you are the one left holding the bag.
That is exactly correct. When Fed governors explicitly use the word “unlimited,” I don’t know why people have such a difficult time understanding what unlimited means.
LOL. This will only make big banks even bigger. Not to say there is now zero incentive to save and produce. People will just consume to no end, knowing that they can forgive their own debts from time to time.
But hei, I actually like this proposal. Anything that can make Murica collapse faster, I fully support.
Monkey, I hope so. I’m so disgusted with this country at this point that I want it to collapse so the people learn some pain and hopefully wont’ repeat these mistakes after it’s rebuilt.
Sort of, borrowers won’t gain much if this system continues. Credit to the plebs is really tight unless the credit advance is for some consumer item.
If there is a great reset which will not be for the benefit to the borrower, the
borrowing of anything (unless tangible) hard assets is and has been foolish.
-k
RightNYer, unfortunately history says otherwise. We had the depression where afterwards people learned to be conservative, and then it took only 50 years for people to revert back to their old habits.
Americans love to spend. Generation Z has to live within their means because they have no money and lots of debt not because they understand the value of money.
I guess we’ll see. I don’t see us getting out of the coming depression as easily as we did in the 30s, as we were a lot more culturally homogeneous then.
RightNY,
“so the people learn some pain”
The addicts may need pain, but the pushers must be executed.
Cas127, fine with me.
You are really overestimating the intelligence of the masses. 95% of people have no idea what you are saying.
Try using the phrase “Bread And Circuses” in a group of average Americans. Probably not 1% know what you are talking about.
I had to look it up. I’ll save other’s the time.
https://en.wikipedia.org/wiki/Bread_and_circuses
Not a difficult concept, and I would say both bread and circuses are very complex now, and commercialized/financialized almost beyond FN belief. Paulo put a lot of it in one sentence above.
Few know what they really need for “the good life”, (or even wonder/think about it), which has also been debated since way before the Romans.
We need a Green New Industry AND the Value Reset that goes with it.
Politically, America appears to be more and more Balkanized, but ultimately, there are only two classes; the creditors and the debtors. For every creditor there are at least 90 debtors, and, as the Fed continues to rule by monetary policy, the members of the debtor class grow even deeper into debt. None of the is by accident, and debt has become an addiction.
When Trump said that he was the King of Debt, he was speaking to a country that had already become a kingdom of debt.
You can structure your life where for the most part you are not a debtor or a lender. You can own your dwelling. There are a very few public companies with zero debt, so you are the equity owner. You can hold savings in precious metals outside the banking system. You still will need to pay bills in debt based fiat, but you can keep it to a minimum. It means you live an unleveraged life in a leveraged world. It’s a lower standard of living, but safer if world spins out of control.
Old School,
I would posit that living an unleveraged life is a higher standard of living. There are pros and cons to having a modest home that’s owned free & clear vs having a luxurious home with a mortgage.
If one is young and ‘rising up the ladder’ with higher future income on the way, living large and leveraged may be the way to go. Certainly, after WWII that was America’s identity and ethos. Big suburban house with two cars in the garage etc.
On the other hand, living with no debt and having a cushion to fall back on – if needed – gives one piece of mind. To me, that piece of mind and the lack of stress & worry about making payments is the foundation of my ‘good life’.
“If you can’t pay for it, you can’t afford it.” Words of wisdom from my dad that are as true today as when he said them half a century ago. So now I say these words too …
Dan,
“an unleveraged life is a higher standard of living”
You can eat very well or sleep very well. But you can’t do both.
Cas127,
After making this comment, I thought it was perhaps too much ‘soapbox preaching’. As a kid though, I was programmed against ever buying anything except a house on credit. That has certainly stayed with me, and looking back, it has served me well (like it did my parents).
As a result, I now eat very well and sleep very well, and in fact I can do both, but not at the same time, eh.
Dan,
Eat v. Sleep is the old (wise/honest) stock broker’s saying…emblematic of the risk v. return trade off.
A person can either eat well (thanks to higher risk/higher return investments) or they can sleep well (thanks to lower risk/lower return invts) but no one gets both.
Any pretty much every honest analysis of investments bears this out.
There is a *reason* why higher return invts come with higher risks…it is because the promoters *have to* offer higher returns to get enough people to come on board the crazy train.
Too many civilian investors believe there are free lunches when it comes to return v. Risk.
There aren’t…any “good deals” are snapped up immediately by the promoters/insiders.
The general public are left the refuse and to essentially gamble against one another.
Cas127,
I should have picked up on the old stock broker’s statement. Learn something new every day on Wolf’s site …
Right on the money OS!
And I can add that the satisfaction, peace of mind, and lack of stress that follows is worth waaayyyy more than all the toys, etc., from hot cars to hot babes that have ever occurred or been experienced vicariously or otherwise.
I encourage all on here to get to that place of no debt at all and at least try it as soon as possible; and then, IF you decide to go back into the debt trap, at least you will know the difference and be making a conscious decision rather than just another reflex.
Also suggest this is a subject worthy of extensive discussion BEFORE any kind of long term hooking up with any partner, as well as extensive as possible discussion with off spring as soon as they are capable of understanding the concepts involved.
VVN, when I was young, had hot cars and hot babes, I didn’t have any stress, just loads of fun! LOL!
Vintage and others:
“Being debt free” in the long run will mean that most of the world will end up homeless. Prices may crash but the majority of the globe will not even be able to afford food.
Period.
It is the nature of the capitalist beast.
Prepare your children and grand children for the upcoming new dark ages.
Is there anyone on this blog that believes that the present situation is sustainable????
Humans are too susceptible to the “7 Deadly Sins” that fuel capitalism.
There is no outlet door to “something better” because too many are not interested in anything “….getting it now before anybody else”.
The foolishness and stupidity is colossal!
I’ve been cheap my whole life, but I didn’t really understand what cheap meant until I got married 43 years ago. My wife is CHEAP and I’m a very lucky guy.
Lucky you, Dave. I love frugal women. Those spendthrifts that jack up the credit cards for the closets full of clothing and expensive purses give me the heebie jeebies.
Somebody should gather the three of y’all’s comments, along with a lot of Paulo, and make it required reading for everybody between 10 and 80.
Also: I blame “reality” TV for some of this. It’s not just the “real” housewives stuff, it’s almost everything on HGTV and the other house shows. When I see these 20-somethings demanding the kinds of things I didn’t even know existed, I can laugh. A contemporary of theirs would think it was perfectly natural.
Clete-very well-said. It makes me again wonder if the acme (decline ensuing) of any society is when it reaches the point where it develops a large ‘entertainment industry’. Subsequently, an increasing number of the population seems to take its eye off of the ball, and in the resultant, ongoing wreckage keeps declaring ‘…who knew???’.
may we all find a better day.
Automotive News has reported that it was a very good year for motor vehicle dealers with many seeing record profits.
I wonder how much PPP loans had to do with their record profits. Automotive News has not made any mention as to what impact this had. When information became available on the amounts loaned to businesses, I checked how much dealers received in my city. The largest dealer group which is owned by a classmate who brags about how rich he is received 7.2 million dollars. All the other dealers also received millions.
Not sure about PPP loans, but prices had a lot to do with it. They soared.
They miss the point of direction of the story, and went off in some tangent from personal experiences. Just sayin,
-k
Nels Nelson,
I don’t think ppp loans had much to do with that. PPP loans were supposed to be equal to 8 weeks of an average payroll period from the last year. Because many businesses had less business then previous years and less employees, while many small businesses did end up paying their remaining employees a bonus from it. It didn’t last past the ppp period. Some small business employees were given upto a 50% pay bump during this period, it tended to be less than that. This upcoming time employers will have a longer? time to spend it and have to spend a smaller percentage of it on payroll, so I expect those bonuses to be smaller then last time. Last time employers had 8 weeks to spend it, but towards the end, this time period was extended, when a business got ppp loans was also a factor.
When the higher unemployment was announced, MANY employees at small businesses in my area “quit” and their employers did say they were laid off (so their employees could get unemployment), because business was plummeting and they hoped to get these employees back when first lockdowns ended if business recovered. If those employees hadn’t quit, many would have to have been actually laid-off. Those employees who quit made a lot more money than those who stayed and got ppp loan bonuses. A small number of people were “laid-off” continued to be paid under the table and also got extra unemployment money, these more entrepreneurial people were rare though. Some of the more ordinary “laid-off” people bounced between jobs and gigs that paid above what they were used to between unemployment periods. Some “laid-off” people went back to their previous employer or started a new job when unemployment first ended.
You must be living in a dream world.
And I’ll leave it at that
No keppered I’m not. That’s what happened in my average midwest mid-size city. Real unemployment is still currently near zero in my area, but, just like everywhere else in America, we could be about to go through a very nasty recession (not sure what you would call whatever we are currently going through). Many small businesses are on the brink just like everywhere else. Not a dream, believe it not.
“ American consumers – those hundreds of millions of mythical creatures whose sole job is to consume more than they make – have paid down their credit cards again.”
My reaction to this line when I first read it was equivalent to: “you bastards, you killed Kenny.”
The problem with the policies from our wonderful leaders is simply that they are devoid of sense, it’s not ever about what the policies incentivize, or how would this affect people and the country in general, it’s only about how does will sound bite work in the media or how does this help me get re-elected.
And how will this make myself and my worthless offspring more?
I’ve been trying to guess the approximate year when our leaders replaced foresight with myopia.
LH-again! (you’ve made me spray my coffee on the keyboard!).
may we all find a better day.
Or at least a better (sealed against coffee spray) keyboard…
And totally agree with your comment in praise of the wit and wisdom wittily expressed from the hook leaser!!
We need a new virus every year. In 10 years, consumer credit will be zero.
Eat that Ben Bernanke!!!
Some please wake the fed up, and tell it cutting rates ain’t increasing debt as it think it’s supposed to. “Paging Dr. Jerome. Please pick up, Dr. Jerome The circuits are busy.”
If I had a dime for everyone who posted a comment here, that we simply can not raise interest rates no way no how, because the house of cards would collapse…I’d be a dozenaire or a hundredaire.
Yet here we are, cutting rates, and debt is being paid.
That’s not supposed to happen. The peasants are supposed to go shopping.
Of course “we can’t raise rates because reasons” is bullocks.
Because, you know, yes we can.
The problem with raising rates is not as much a problem for the consumer as it is the US Government. They are all tied up with ultra low rates for all the borrowing and the duration of those loans in largely <24 months. So what will happen when the treasury rate begins to tick up. Yep government debt costs will SOAR. That is one reason to keep the rates ultra low
Exactly.
On a side note the median interest rate on credit cards on 1/3/21 was 16,1%
The government can simply default and investors will have to eat it.
It is not so far back, 1980’s, where sovereign defaults were happening somewhere every two years or so. Even in “civilised economies” at the time, mortgage bonds were considered safer than government bonds.
It has something to do with Basel II and III that sovereign debt is a sacred artefact, but, it never was in the past and it does not have to be so in the future. It is just politics.
The rates will rise when the accumulation of assets in the custody of the supreme leader is complete.
My friend Timber’s,
We have gone over this many times.
There is no possible way to raised rates without causing hyperinflation outside the banking system.
Do you think that’s because all the savers will suddenly have more income to spend? /sarc
What to do then? I don’t know since the government is planning on giving 2Trillion dollars on top of all of last years stimulus. Is the plan then to inflate the prices of everything to support asset holders whom would have otherwise lost everything – to savers who, like me, were planning on swopping in when the market declined? But now injections of cash has utterly destroyed the calculus. There has to be a measure of this madness.
But the euro to dollar is 1.20 but gold is holding at 1800 and platinum remains at 1000.
What is correct?
Realize we are in a new place with the money printing and how it will play out is unknowable. Don’t get sucked in to doing anything stupid (like putting all your eggs in one stock for example). Basic personal finance still applies. Have a big cash cushion for emergencies. Don’t borrow for consumption. Don’t stretch too much when buying a home. Excessive leverage gives you the good life in good times and destroys you in bad times.
I’ve been doing this for years, and now I look around and realize I was the sucker while everybody else levered up and got stupid wealthy.
OS, I think the effects of money printing is knowable. Just look at the recent financial history of Yugoslavia, Argentina, Venezuela, Zimbabwe, and yes Germany. And others I’m too lazy to look up.
Hernando,
Since we don’t know how this will play out, (I’m betting on Inflation, Jimmy Carter style), the best thing to do now is to buy CDs of 1 year duration and suck up the low return for now. When interest rates rise then you can roll over the CDs at the higher rate. Interest rates cannot go much lower without going below zero. Already, they are 3 to 4% below the rate of inflation. But better to lose 3 to 4% than lose 30 to 40% in the next Bond/Stock market meltdown. With a few exceptions, there is no decent risk free mid/long term investment in the stock/bond market. If you want to play in the casino, be my guest. I’m not playing in that game.
That’s sounds like a good plan. At some point stocks will become a bargain again, but if your money is locked up for a year at a time it will probably keep you from jumping in too early. Real bull markets are long term runs and you don’t have to worry about missing a few months. Best to make sure as much as possible bottom has been put in.
‘Real bull markets are long term runs and you don’t have to worry about missing a few months’
Checkout DJIA between 1964 and 1982.
DJIA was near 1000 in 1964. (imagine you retired in that year)
DJIA started tanking down and got back to 1000 around 1982!
18 years of NOTHING!
1982 to 2000 was a great bull. Bear mkts cuts short in 2000 anf again 2008! S&P zoomed from ’09 to ’20 over 350%! thanks to Fed?CBers!
If one thinks another BULL is take off NOW, at these nose bleed evaluation, good luck!
The coming bear mkt(?) will be an event of a life time for many new bie investors. I hope I am wrong.
(Been in the mkt since ’82)
Sadly, time-honored laws of economics that we expect to be followed today no longer apply in this carnival house of mirrors maze we call today’s economy.
Savings, avoiding excess debt, living within your means, and being productive in the sense of producing more goods and services than you consume are no longer important publicly and privately.
Sage economic observers smarter than us have for years cautioned that this house of cards simply can not go on and will collapse on itself soon– only to be proven wrong again and again.
I truly believe that those in charge are certifiably insane (willfully divorced from reality) and will attempt to keep the game going until all is kaput.
“We are all aboard a speeding train driven by an insane engineer. The best we can do is retire to the dining car for drinks.”
Better plan to combat inflation; Buy everything that you know you will use for years ahead.
Save on gas, avoid lockdown shortages and exporsure to viruses.
Stock up on household supplies, non-perishable food, clothing, garden supplies. Envision yourself never having to go to the store during the Biden administration chaos, except for fresh food.
“…..the Biden administration chaos”? Thanks for the laugh!
As for the multiple people hoping for the country to collapse. You are insane. You’ve never lived through a country “collapsing” or you wouldn’t say that. I hope you don’t get your wish…for all the obvious reasons. Reform without anarchy is an option.
Timmy-good advice, if one is able to. Chaos, though, has been with us for decades (‘guns and butter’-personally or nationally- hasn’t been sustainable from its inception). nodecent-too many appear to lack an understanding of the serious effects contained in the old cliches of: “…just throw the baby out with the bathwater…” or “…we really need to reinvent the wheel…”. Neglecting ‘proper maintenance’ (implying, of course, there is one, and that all concerned are using, the same ‘service manual’) of ANY system ultimately results in extreme unhappiness, if not downright tears…
may we all find a better day.
My CU offers 13-month ‘bump up’ certificates; which allow one interest rate reset and/or one additional contribution over its duration. I got one at 2.5% in early ’18, and felt pretty good about it as rates tanked (obviously, I didn’t partake of the interest rate ‘reset’). Now, the CU is offering them at 0.5%, and I may roll into one in a couple months if rate hikes seem imminent.
Individual high quality bonds held to maturity are probably not a bad bet. And short term bond funds wouldn’t be hit too hard either in a rising rate environment, because the existing bonds losing value would be offset by better returns on the newer bonds. Long term bonds are at most risk for sure.
Personally I would protect every thing that I own from thief’s and inflation.
Then I would start with a financial revaluation to include inventory (personal holdings) and digital (banking) holdings.
Then I would (if you have not already) decrease personal reliance on digital holdings.
I would allow a certain percentage of wealth (carefully) and as a working hobby to play the markets.
I would become my own banker.
With the one purpose of turning every piece of funny money into a tangible hard asset. No mater what currencies flow in.
I would play the game carefully knowing that the central bankers have become both lenders and thief’s, that there is not anyway to stop the crooks.
So knowing this criminal enterprise is rigged beyond your repair play along always tucking a bit away for yourself and love ones.
There are many voices online, in print and locally which heed this call.
Let’s not forget healthcare debt. It shows up somewhere.
What goes up, comes down. Well, not anymore… as gravity was not playing ball and got canceled.
……..another way to look at it, people are lowering their debt, personally or by Government subsidy and not limiting the supply chain of goods or services. Car makers have plenty of resource to make more new cars as does many manufacturers and services. Business shouldn’t have a problem ramping up production if there’s a surge in government and consumer spending. I don’t see inflation rising above what it has been. I think rising interest rates would be a benefit for earners, usually wages rise and savers, 1 or 2% isn’t worth it, and possible deflation.
re: “Car makers have plenty of resource to make more new cars …”
Not really. There’s a ‘chip shortage’–cars are as much about ‘connectivity’ as transportation these days–and Ford can’t even produce enough of the golden goose F-150 as it could sell. All the other manufacturers are in the same boat.
Yep, those costs seem to be supply side…I bet car prices will start to outpace those quality adjustments when it eventually makes its way downstream.
Seems like the car manufacturer’s goal is to get you from place to place with as much comfort and entertainment diversions as just staying in your living room. But try to get a bare bones ride, and you cannot. Dealers all say,”These are the features people now want”
Which makes for very poor “situational awareness”, badly needed on the road to prevent accidents.
Hence the logic in spending lots of money on”self driving cars”, or various electronic “save yer ass” driving aides as our mobile living rooms continue to improve.
NBay-good observation. The ads that show the proud owner’s new vehicle avoiding certain doom from a forward/sideswipe collision never seems to address the possibility and consequences that a following vehicle does NOT possess the same technology…
may we all find a better day.
91B20-
Per our other discussion;
Maybe everyone should be forced by law to ride a bike for a 6mo/year before getting a license to control much higher masses at speed? Look at what is required for big rig drivers.
Would give them a more intuitive grasp of the energy of the physics involved, that every driver should have.
It has been estimated that the US has spent 5 or 6 trillion dollars on its unwinnable and on-going wars of choice and aggression around the globe in the last decades….
Is 1.9 trillion really a lot of money?
priorities…
And we’ll have spent $6 trillion in under a year on COVID “relief.”
1.9 trillion dollars is chump change compared to the $21 trillion that went missing in federal budget between 1998 and 2015– this is well documented by researchers outside gubvarmint.
You are absolutely right. The MIA and these wars have bankrupted the country. Then you include things like unchecked immigration, generations of welfare, corporate welfare, excessive spending, etc.
No wonder this place is falling apart. You can sense this, and now attacks on free speech, attacks on our history, and free for all voting.
Ah, it’s all gonna be ok! /sarc
The attacks on free speech are a response to the disorder. They want to suppress any speech that calls attention to what’s happening. Immigration is the number one contributor to our problems, in my opinion.
Looking back it’s pretty clear the government intentionally ran an immigration policy they were afraid to pass thru Congress because majority of voters didn’t want it. It corrupted the rule of law and created massive unrest in the country. If we needed more immigration, politicians should have made their case to the American people and explained how it would benefit us. Instead we have 20 million people who live as semi citizens.
RightNYer:
” Immigration is the number one contributor to our problems, in my opinion.”
Let’s then start with dismantling the Statue if Liberty!
IMMIGRANTS BUILT THIS COUNTRY! (Sorry to “shout”!)
Without “immigrants” most countries would end up with the “Royal Blood Disease”!
And, if we would stop devastating the “southern” part of our hemisphere dismantling legally elected governments because they refuse to become American subjects, maybe we would have less of their peoples wanting to flee and enter our country!!??
Our history is sopping with the blood of immigrants who were used by American business to break organized labor gains, and, of course globalization threw the whole process of labor gains into the global toilet.
Too many Americans are just too backwards when it comes to the real history of our country, here and it’s actions around the world!
Sierra, I’m not going to respond to this fact-free propaganda.
Sierra7, my grandparents came from Lithuania through Ellis Island and registered as immigrants. They had a job waiting (in a coal mine). My Dad fought in WWII, and I fought in Vietnam. We are Americans and proud of it. No one in my family ever took unearned money from the state or federal government to feed ourselves or raise a family.
The folks coming across the boarder are not using the same process. That’s all I’ll say.
Immigration? Are you nuts? Immigration is the foundation of our country’s success. Our problems are related to out of control government spending. We need more immigration, if anything, to pay off our long term debts. But let’s find a way to make it legal.
@Anthony A,
The grandchildren of the people hopping the fence now will be just like you in 90 years, the only difference is we had a way for people to legally immigrate 100 years ago, and we’ve made it way to hard to legally immigrate now, so people hop the fence. They are breaking the law because the law doesn’t allow for the demand for US work and citizenship. If the party in power actually cared about this, they would do something, but they don’t, and won’t.
Why do you need or would you want immigration in a shrinking economy? Because in my mind its only been growing on paper since 2000. If you want to make lives worse for the people already here not in the top 10%, then by all means invite more people in to fight for the shrinking amount of jobs left for the 90%. If we have functioning fusion power in the next two years, i’ll change my opinion. But unless you plan on replacing fossil fuel with slave labor, i can’t see any reason to increase the population when total energy and total economy is shrinking.
Happy1,
“the only difference is we had a way for people to legally immigrate 100 years ago…”
Not true. We have a legal way, today, now.
“They are breaking the law because the law doesn’t allow for the demand for US work and citizenship.”
No, they don’t care what the law is, or is not. They are “breaking the law” because they have low wages in their countries, than here.
“We need more immigration, if anything, to pay off our long term debts.”
We don’t need immigrants to pay for anything, let alone long term debts. We have a sovereign currency. It is impossible for us not to pay debts because we always and everywhere can.
“We need more immigration…”
Sure, if you want to drive down wages and impoverish working folks, live we have been.
I spent 15 years and 100s of thousands of dollars in taxes to get my green card.
I have full sympathy for 20 million illegal immigrants here but I can’t condone the path to citizenship for them when we still have millions of legal immigration waiting for their turn to get their permanent residency
I have never liked the kind of people who cut into the front of the line, no matter what their self-rationalized excuse.
RNY-i’ve said it before, will say it again-there’s a macrohistoric situation going on here, one of population vacuum (in this case a perpetual U.S. demand for a low-cost labor population). (Roman Empire as one example, trading low-cost, motivated-by land promise-immigrant replacements for declining levels of indigenous Legion enlistments. From another angle-postwar German recruitment of Turkish ‘guestworkers’, might be considered a more honest national approach to the issue).
(All this to say, vacuums suck…).
may we all find a better day.
Right-
No need to, it’s just a response to yours.
Fiat money printing has helped create a society where personal responsibility is being replaced by it’s not my responsibility victimhood. Probably number one key to success is attitude and the ability to delay gratification to achieve a goal. Now delaying gratification is penalized with negative real rates and debts are socialized. Prosperity is a summation of individual efforts not centrally planned from above.
Big problem with money printing is politicians can not be trusted to not to bankrupt the country with excessive spending.
Politicians won’t bankrupt the US. However, they will destroy the paper currency, without a doubt. They’ve destroyed a paper currency 3 times in our history already, 4 if you count the currency of the Confederacy.
Does anyone monitor GINI coefficients? I suspect our policies the last 40 years have contributed to its rise over that time , 34.5 in 1979 to 41.5 in 2016 (World Bank estimates its risen to 48ish now). This represents a massive redistribution of wealth! And nobody talks about it, nor whether this contributes to our social and political ills.
I’m going out on a limb and say yes it does.
Globalization has decimated developed world’s labor market bargaining power and therefore corporate profits were at all time highs the last few years. MAGA for good or bad caught fire because of labor issues of working class. There is always a tension between corporate profits and labor bargaining power that must be hashed out in the political arena. Supposedly corporate profits is one of the most mean reverting statistics there is. From my memory if tends to swing between 5% and 10% with mean being around 7.5%. If profit margins swing from high to low % that would cut the E in the PE in half and probably knock the P down a lot as well. Could be how we get to 70% stock wipeout.
Let’s also not ignore the supply shock to the labor market over the past 50 years. It is wonderful to have greater diversity and equality, but businesses did not increase headcount or salaries accordingly (nor should they be expected to).
Rising CPI inflation tends to compress profit margins.
But in addition to that it leads to higher rates, which means that there has to be significant deleveraging as corporate debt is at record highs. This further lowers profitability and some corporations will have to issue more stock when debt becomes to expensive to roll over.
In addition to that, rising rates also means that the whole TINA framework falls apart, because stocks are then expensive relative to interest rates/ bonds.
So IF we get significant CPI inflation, this will be the perfect storm and we could easily see -70% off the S&P500. Shiller P/E is currently 35. 70% off means it goes to 10.5, which is actually a not an extreme value at the bottom of a run of the mill bearmarket, historically speaking. (it would be about 33% below the long term median value). In 1982 it reached 6.7.
I’m not saying it will happen. After all, it would be a once in a generation type event. But stocks would still not extraordinary cheap after such a fall from current levels.
IF the Fed does allow a drop greater than 10-20% in the markets, I’d guess that the SP500 would be hard pressed to fall from 4,000 range to 2,000 as at a 50% drop, I could easily see the Fed step in and start buying “SPY”, and other market ETFs. The entire world economic construct falls apart if the US markets and economy fall apart, due to reserve currency status, etc. The Fed will step in to “Save the World”. I understand 70-80% drop fits history and would be the natural mean reversion, but the Fed can stop history and nature from happening with electronic zeros and ones injected into our current economic simulation.
I don’t see the political will to allow the Fed to buy stocks, no matter how bad it gets.
Fed policy of artificial low rates ribs from elderly poor and gives to asset holders.
The govt is talking about “baby bonds” for newborns. If I was of AARP age, I’d be petitioning for the govt to create “Senior Bonds” for anyone age 55/60 ish and older, paying 3% minimum like the baby bonds bill specifies currently.
What happenned to the united voting power of the AARP? The seniors need to unite, and I plan to put my donations and efforts behind such ventures once I get closer to that age myself. I can not see one major issue with instantly creating “Senior Bonds” paying 3-4%, with an income cut-off at 400K per year. Yet perhaps the govt knows the can not control seniors without making them dependent on govt handouts…thus they fear letting seniors be financially independent? There must be some reason the govt want seniors to suffer finacially…is it a vote control scheme???
Constitutional (and plenty powerful IRS mandate to enforce it yearly) of say, $10-$15 M max household net wealth would make a LOT of problems vanish. More so than a minimum wage, and a lot of other band-aids, I betcha. Of course I think a Green New Industry on WW2 scale is needed, also, along with somehow addressing ZPG after doing the first two and having a new perspective on things, as it is a really tough issue.
Alternate to doing all 3 is pretty ugly, sooner or later.
NBay-Interesting and thoughtful proposals, as usual. Your last sentence, though, again illuminates the seemingly flat-proof wheel of history…
(ref: LH’s ‘…leaders replacing foresight with myopia…’, earlier).
may we all find a better day.
One big difference in that wheel of written history, and that is Dr Oppenheimer’s “gadget”.
Leaders/policy makers (and friends/loved ones) for 10,000+ years (of ‘civilization”) used to be immune to the results of any of their choices (whereas the peasants never were). Not absolutely so anymore.
The major leaders are now reduced to “proxy wars”, as we both know well.
They may even develop the foresight to abandon the old ways, even if for their most basic power grabbing selfish reason, e.g., their own survival.
NBay-same sentiments. Just wish there were more first-rate ‘power-grabbing selfish’ minds (‘noblesse oblige’ was the old-term, i think) among them rather than the second/third/fourth-raters we seem to have in proliferation (ones who don’t truly get the power of the gadget, or of the human life-support limitations of our current and actual spacecraft).
may we all find a better day.
1971 remove gold backing, step back and watch the insanity grow and grow, ALL the financial problems, repeat ALL of them have their cause directly or indirectly in FIAT money, simples.
Completely agree
Cash out/HELOC has to be a driver. Per Freddie Mac here are some stats. Q4 2006 it peaked at $89.9 Billion. It dropped as far as $7.3 billion Q1 2014. It was pretty level until Q3 2019. Then you see a big jump in 2020. Q3 2019 was $37.4B and Q3 2020 estimated at $59.2B. I suspect it will rise for at least a few more quarters.
The number of vehicles on the road has been increasing. The ratio of commercial vehicles to personal vehicles has been increasing. The median age of a vehicle has been increasing.
I observed some people will try to pay off their loans as they approach retirement age. An American living to the age of 65 might expect to live to be 83 – 86.
LoL- just got my latest offer from Citibank- I can borrow at 4.3%APR for 16 months- so what should I buy?
Silver coinz?
LoL- or I can just have a zero balance.
Seriously folks, what we don’t expect is a real interest rate.
And a real interest rate of say 3 percent paid on bank CDs would be a stunning thing in today’s ZIRP world.
On the other hand, speculation is puffing everything up, and when liquidity dries up, pffffffft asset prices.
As we tend to forget. Right now cash is trash, but it shall once again be king. Or we inflate to infinity and beyond!
All I know is that hyperinflation is right here, or so I have been told for 50 years plus. And it still ain’t happened because all teh furriners keep soaking up everything we print and demand more.
Sigh. The mall jingle mail is more interesting, because debt was destroyed, which ain’t supposed to happen in hyperinflation because we was supposed to pay it off in forever stamps.
Gold is near all time highs, but silver ain’t. Humph. Still waiting for Godot. But 4X since 1999 ain’t bad for holding some value.
Houses. Sigh. Another bubble, totally dependent on interest rates.
House now roughly equal bonds, and will be valued like treasuries.
Of course, someone pointed out that pesky Gini girl and showed that we might just get some real socialism to even our society again.
What is old is new again, and the populist/socialist urge is strongest when young folks see insurmountable obstacles placed in the way of getting to that middle class mirage.
Someday this war’s gonna end…
We haven’t been doing the insane printing that we have in the past few years for 50 years though.
What’s not happening/going to happen is the ability to throw cash into high yield T-bills/T-bonds, bank CDs and money market funds, which was possible in mid-70s to early 80s. The Fed and the banksters have removed those havens to ride it out.
From what I read Fed buys mostly treasuries and that fills the world with cash that they hope burns a hole in your pocket til it is spent. But I am not so sure if that is the plan, that an individual should spend it. Maybe an individual should cut back consumption the 2 or 3% they are repressing you and hold cash for a better time to spend it aka recession. If stock market is going to fall 50% then you can sit on cash maybe up to 15 – 20 years and you will be better off if you can buy in recession.
Indeed, cash is a better deal than it looks on the surface, because it has an option value. If you can buy stocks in a few years time at -50% of today’s price, cash would prove to be an excellent investment.
Every time one of my banker’s wealth department tries to get me to invest money with them “because you’re losing to inflation” I tell them “that’s just an option premium!”
Yes! That’s it, I expect. Suffer a bit now with a 0.5% return on your cash and win later when markets take a dive. Not going to get all stupid and put my dry powder into Bitcoin and whatnot. Just going to wait. I don’t really think it’s all that “different this time”.
But what do I know? There are almost as many predictions as there are comments here. Nobody’s got the crystal ball. Stay diversified and keep some cash, I say.
Stop blaming fiat currency. Blame those who do not know how to effectively use the currency. Biggest misuse is our tax code, which has allowed the One Percent to own most of the nation’s assets. And that cohort is still accumulating capital. That’s the top of the K economy. The bottom is everyone else. Those in recession are making an effort to reduce debt. The most expensive debt (credit cards) first. Recessions increase the rate of savings. It’s not the amount of money, it’s the distribution of money that is important. There will be debt cancellations. Of that I’m confident. Debt that cannot be paid will not be paid. That movement downward will ‘reationalize’ prices i.e. stock prices. And decrease commerce. Don’t know when, just know how it’s going to happen.
Chris’ pragmatic approach is understandable [if not inevitable]: after all, what is “a person” to do in the face of systemic injustice? However, it fails to explain that “a person” stands or falls in the context of “a society” [especially if you believe in markets to provide order] and thus it sustains the very sociopathic behavior [commission and omission] it hopes to avoid … behavior which, “in the end” [“in telos”], drags everyone down. Even Keynes grapsed the vital role of social context when in 1920 in “The Economic Consequences of Peace” he wrote: “Debauching the currency … engages all the hidden forces of economic law on the side of destruction, and does it in a manner which not one man in a million is able to diagnose … fast rendering impossible a continuance of the social and economic order … with no plan for replacing it.” Mustn’t we at least try to do more than suspend our membership in the human race? I like to at least think that keeping us from collapsing into insularity is what Wolf is attempting … by refusing to “accept” Big Brother’s doublespeak. Best.
The crash in 2008 – 2009 and the actions afterward were the tell. That not one banker lost all their wealth after blowing up the system just didn’t smell right then and still doesn’t. Martha Stewart was a bigger person than all of those guys.
Wall Street guys are all cowards, they always pick on women.
Old School:
And, remember: They were doing “God’s Work”.
Oh how that phrase uttered by the most arrogant mealy mouthed Goldman Sachs leader of the time.
As u said, when no-one is accountable then the ball game is over.
American (and possibly globally) financial world: RIP
There’s already debt cancellation going on in CA. They passed a rental assistance program that pays 80% of outstanding rent to landlords if they forgive 20% of the debt. Any tenant can apply for financial distress, pay 25% of rent and get the other 75% wiped out as described. That’s a good deal for tenants, bad for landlords and taxpayers. You can expect landlords will either raise rents to make up for this in the future, or bail out of CA.
I’ve been saying for years rent control was coming to America, and CA leads the nation as usual. Coming to a city or town near you.
Petunia, there is just not enough room in Texas if all these Californians pull out and come here. And I know Florida is getting full too.
I moved to Texas from California 12 years ago and there weren’t any “Don’t California my Texas” or “Welcome to Texas, don’t mess it up!” messages on trucks or t-shirts. It was more like, “I wasn’t born in Texas, but got here as soon as I could”.
My how things have changed.
“Allowed” the 1% to own most assets? Most people in that category worked a full career and sacrificed greatly to get there. It’s a myth that most of the people in the 1% are rentiers.
Now 0.1%, yes, more inherited and unearned wealth for sure.
Alexander Hamilton’s plan for financial slavery was for the Federal government to assume the war debts of the individual colonies thus removing their effective sovereignty and making them dependent on the federal money machine. All we are seeing is the continuation of that slavery scheme as more and more debt is transferred to the federal government’s balance sheet which then simply transfers it on to the Fed. Of course there is no and never was an intention to repay it. It is simply a global tax on all persons who hold US dollars which accrues to the benefit of all persons who owe us dollars. A simple wealth transfer from creditors to debtors. What else could it be?
Hard not to draw present day correlation between Hamilton’s endorsement of a central bank, and Jefferson’s disdain with the Hamilton play being so popular.
Jefferson Quote:
“If the American people ever allow private banks to control the issue of their currency, first by inflation, then by deflation, the banks and corporations that will grow up around [the banks] will deprive the people of all property until their children wake-up homeless on the continent their fathers conquered. The issuing power should be taken from the banks and restored to the people, to whom it properly belongs.”
Implicit,
The answer still exists: Credit Unions. I’ve belonged to one most of my 65 years.
Yep, I have also had Credit Union accts. Lately, cash is king.
Hamilton’s plans are the reason Aaron Burr is one of my heroes.
Haha Yet everyone believes he was a hero with the play being so popular. Haven’t seen it though, so can’t comment about it’s entertainment value.
FYI: Aaron Burr killed Alexander Hamilton.
i found the play very entertaining, and believe a good thing in getting a few more of us interested in our history at all.
That said, have had to spend an inordinate amount of time with my stagestruck 18-year old granddaughter expanding and explaining the back-the as-depicted and the post-stories with her (emphasizing the need to always examine closely the kaolin content of the feet of the immortals…).
may we all find a better day.
Pretty easy to load a black powder smooth bore pistol so it shoots the ball slower and crooked….I could do it.
We’ll never know…..
“Mythical creatures whose sole job is to consume more than they make.” – according to Wolf.
You fighting human nature here.
” Propensity to consume ” – is the back bone of the economy. It directly correlates with the Unemployment and depends on many factors. We are consumers! This task hasn’t been given to us by some proverbial government or Deep State. It’s our choice. We make decisions to consume, save or invest on daily basis.
People still spending money, what a shock ?! Most of americans still have jobs. Interest Rate plays greater role in this. Helicopter Money as well. Mortgages more affordable than ever. Car loans are cheap. People are taking the opportunity while they can.
“Wierdest Economy Ever” … Why is that weird ?
What’s “weird” are the distortions, for example: 10 million more people out of a job, while personal income spikes to a record (driven by government payments) and purchases of durable goods spike to a record and imports of goods spike to a record, even as spending on services plunges. This combination has never happened before in recorded history of the US economy and is therefore “weird.”
It’s not so weird if you look more closely. If a two income family loses both jobs, they get unemployment for two. Whether they own or rent they are not required to pay rent or mortgage, for a long time utilities as well. They may qualify for extended SNAP benefits depending on family size.
So, they have an income while not paying for housing, utilities, student loans, and may also get food assistance. This probably gives them more disposable income than normal.
Exactly this. Millions of people have realized a financial windfall in the worst job loss market in history. This is disgusting.
Need an Aspirin or a Dramamine?
To recap the expansion of credit card debt pre GFC was based on rising home prices, and the need to keep up with rising home values, assuming you could consolidate all the CC debt with a REFI later on. The second part of that was medical debt, pre ACA, medical costs were rising as well, and hospitals were encouraging patients to max out their cards. You didn’t want to go Medicaid and put your home (cash ATM) on the block. The new admin wants to shut down the credit bureaus, and create a govt bureaucracy. The Fed wants to open direct bank accounts with individuals, This overreaching may reflect in some ways the acknowledgment that bank regulations have largely failed to protect consumers. Consumer credit will soon be controlled by a national database and carried out at the lowest possible interest rates. One day citizen Musk may be able to borrow money more cheaply than CEO Musk.
I don’t think the fed wants to deal with millions of customers when they can barely deal with their member banks. Besides, the banks attract better technical talent than the govt, due to pay scales.
Heard an interesting theory that just like people got Fed up with the Catholic church having too much power 500 years ago and threw of it’s shackles for the most part, and got tired of of Monarchs 250 years ago and threw off their shackles, we are coming to the same point with central banks are are going to throw off their shackles as central planners. Time will tell, but they have too much power for unelected body.
The Church didn’t collapse until sex abuse was recognized as a crime and the courts were willing to remediate. Central banks go through the same cursory changes to satisfy their constituencies, (making women priests, or Treasury Dept heads). They could probably take the Fed apart right now for systemic racism. They just need to get Bostic to turn on them.
Paying off your credit cards with 29% interest is like removing a feeding tic from your neck.
Americans are catching on to the banker parasites lending money to themselves in house through their Club Fed, at next to nothing, then marking the money up to usury levels.
Study, locate, identify and destroy parasites in your life and on the body of your society to save our future. Cash is a repellent. Keep it and use it.
I guess that’s easier heard than heeded because everybody and their mother is praising the benefits of debt and gambling these days.
SUV’s are vans by any other name. (Heavens no, it is not a van. Why I can go off road with it. Well, I couldn’t really, but I could drift with it. Well, I couldn’t really….)
But what is driving the purchase of large trucks by folks who are not farmers, ranchers, or tradesmen?
They pull RVs with the trucks. Go to a popular campground, you will see $50,000 trucks all over the place. Camping has become more popular during the pandemic.
Part of it is a mind game. Peoples’ activities and travel are restricted by the pandemic. They feel a personal reward is justified to mitigate the loss.
The deterioration of American highways has made heavy duty vehicles necessary. Size matters, if you are in an accident you would rather be the hammer than the nail.
“But what is driving the purchase of large trucks by folks who are not farmers, ranchers, or tradesmen?”
Sitting up high, feeling of power, superiority, keeping up with the Jones’s, feeling good about yourself, attracts the “chicks”, and more…
“But what is driving the purchase of large trucks by folks who are not farmers, ranchers, or tradesmen?”
Ego. And perhaps trying to make up for certain, uh, shortcomings.
Why does this always come down to some kind of manhood issue?
Maybe like everything else – taste, style and preference changes overtime?
As the owner of an Accord coupe (and 30yr old pickup that was abandoned in my driveway), Like what you drive and drive what you like.
Not many people liking cars much nowadays.
Ask the guys who wrote the all the “Guts and Glory” Dodge Ram truck commercials.
My dirt bike won’t fit in the trunk of my LeSabre.
Hauling boats and toys and RVs, partly. Also handy to put mulch in and stuff if you garden.
Have you seen the TV ads? Trucks will make your lifestyle adventurous!
In the truck ad, the owner is driving across a glacier.
In real life, the truck dweeb is driving across a strip mall parking lot.
No they don’t need trucks. They feel inferior as humans and having a big truck makes ’em feel like a big man. There’s nothing ever in the beds of most of the trucks.
Advertising makes the mouth breathers do what they do….
Lowering Interest Rate will always increase Effective Demand. That’s what we seeing right now. 93% of americans still have jobs. Increase in Demand will lead to increase in employment in distant future (1-3 years). Add vaccine to equation, reopening of services in US, and we get New Economic Cycle, not the Armageddon every one is waiting for.
Decrease in CC Debt is a positive, not negative thing. It will create room for future borrowing, and significantly improve Banks Balance Sheet.
“93% of americans still have jobs.”
To be more correct, we would say 93% of people in labor force have jobs.
The employment participation rate is another story altogether.
Participation rate is percentage of working age population who are in labor force. As of Jan 2021 that was 61.4% officially.
So almost 40% give or take, of adults are not working according to this definition. That is historically low.
So no, 93% of Americans do not have jobs. It is probably somewhere in low 60%.
How are retiree people classified?
@Joe – Unnecessary, unneeded, and a drag on the economy with their thoughtful limited spending and constant whining about interest rates.
Drunk Gambler,
“93% of americans still have jobs”
I guess that’s not what you meant to say. What you meant to say was that 57.5% of working-age Americans have jobs:
Of that “46% of Americans still have jobs” — 150 million Americans have jobs of 328,000 million Americans:
At some point soon Americans will realize that liquidity does not create jobs. It doesn’t seem to create much inflation either. Government has realized it…a bit…hence all of the spending on top of the QE.
The velocity of money is small and short-lived with unearned liquidity.
The stuff coming out of Washington reminds me of the Bread & Circuses strategy of Ancient Rome where the thought was that if you kept the serfs happy with bread and entertainment, those in power could stay in power and debase the currency at will. Of course, this was just before the Fall of the Roman Empire.
American politicians and Fed Governators obviously were absent during Ancient History class. They are killing the purchasing power of the Dollar just as the Ancient Romans progressively reduced the silver content of Roman legal tender coins. We must think BIG says Janet Yelling (sic) in the latest and greatest $1.9 Trillion money printing exercise out of Capitol Hill. As a Keynesian acolyte, she just doesn’t know any better. But her’s and others lessons are coming up fast.
Well, we all know what happened to Ancient Rome. Folks, the barbarians are at the Gates, but they are all dressed in Armani suits!! I wonder if historians will be allowed to print the absolute stupidity that reined in America during this period??! I should be flying my American flag upside down as a Sign of Distress.
Alas there is no Alaric. There are no Visigoths to the North. We are doomed to attrit to oblivion.
For once LH, i gotta dis agree:
There are plenty of such current versions as/of the goth types you mention,,, waiting at the gates and on every border of USA and every other ancient regime,,, to, once again, take the place of all the/we sloths, fat and lazys, and each and every one of WE the PEEDONs who have not kept in shape physically and financially as we have been clearly warned to do for the last four or five decades since the awakening warning of the VN war,,, such warning clear inside USA,,, and the devil take the hindmost,,,
AKA those of us not paying any attention of that clear marker of the end of the empire SO similar to the many other empires that have come and gone for the last 1000 year or so,,, and likely many other empires now lost in the dust of antiquity.
As is common, according to contemporary literature of those empires of record, nobody wants to see until it is too late…
And SO IT GOES, once again
VV, I somewhat agree with you. It’s obvious that we are our own worst enemy and have been for quite some time. FWIW: I haven’t seen any masses of Canadians marching south to the promised land. ;-)
It’s the weirdest economy ever, courtesy of the weirdest monetary policy ever. All you have to do is look at the housing price chart and the GINI coefficient.
To phrase it more precisely: It’s the most rigged economy ever, where ownership, not production, is rewarded.
When hard work does not produce reward, it’s time to change the rules of the game.
See also, the British in Ireland.
Cantillon went on to discuss how money would flow, basically noting that people, (wall street and billionaires), first in the line, (to the Fed), would spend it on luxuries ,(mainly assets), prompting a general rise in prices. Eventually the money would get out to the populace, (trickle down), but until it did, working people would have to pay higher prices without access to the new money, so there would be inflation, together with an uneven distribution of purchasing power. (the 1%).
Meanwhile today on Face the Inflation…I mean Nation:
“Yellen…said that low-wage earners, minorities and women are suffering the most and could face “permanent” damage from a prolonged slowdown” so we need to pass the big stimulus package.
Because if we pass a $15 minimum wage by 20??, those suffering the mostest will be able to afford the mostest of all that cheap real estate Jerome created with ZIRP and QE.
Why, just ask Mary Daly at Fan Fran Federal Reserve. She’s helped create millions of good paying jobs by supporting eternal QE and ZIRP. Jobs that probably almost pay $15/hr.
Janet Yellen is fighting for low income folks, helping put them into affordable home ownership – like modified corrugated boxes, shipping freight containers, etc.
When I used to work in Trinidad, we used to say you “made” the middle class when you had tin on your shack walls and roof instead of cardboard.
Maybe Yellen has been in Trinidad and seen the countryside.
couple of replies aa:
1. the Permian Basin alone is somewhere around 75-80K Square Miles, or approx half size of CA, so most of the folks in CA would fit there without any problem except maybe a bit of water
2. try driving across TX in a small car, and you will quickly get to realize one of the major advantages of a full size pickup truck, as one will almost always be right on your tailgate if you are going less than 20 miles per hour OVER the speed limit, and even then sometimes
ok, back to the so far super bowl, the only game where we turn ON the sound when the ads come on–LOL
VVN, I lived in Midland for a couple of years when in the oil business. Yes, the Permian is pretty good sized, but most of the land is used for cattle ranches and those guys won’t sell to anyone from out of state! LOL
“Yellen…said that low-wage earners, minorities and women are suffering the most and could face “permanent” damage from a prolonged slowdown” so we need to pass the big stimulus package.”
She is selling the poison branded as the elixir. This woman is evil personified.
Govt has 3 options to get out of this mess:
1.) Cut spending (ok you can all stop rolling around on the floor holding your guts, laughing uncontrollably.)
2.) Raise taxes (now stop rolling around like that — you’re gonna hurt yourselves. I know. I know. Rich people will just hide their money.)
3.) Print money!
Which one will our govt choose?
That’s easy….#3
And by the way….Got Au and AG ??
Aunt Yellen and Uncle Sam are now negotiating how much free money to send you at the tune of $1,400 per person, so $5,600 for a typical family of four.
Aunt Yellen says you are wealthy if you make over $60k ($120k per family I assume). Others super intelligent policy makers (sarcasm) think $50/$100k is rich…yet some other wise Uncle Sams think $75/$150k is the magical sweet spot.
In the end, Uncle Sam and Aunt Yellen will pick winners and losers, and it will anger many to the point that we will likely have another total govt red vs blue reset in 2 to 4 years and thus more extreme future govt policy uncertainty…
Handing $5,000 to $50,000 (student loan elimination bonanza) will create even more winners and losers, and at this point I can only assume the hidden intent of the fed and govt is to make sure the population is busy being envious and hateful to each other, and not turning their focus instead to the true anarchy makers…the Fed and govt agents that constantly pick winners and losers while suppressing free makets and a healthy, independent, community based society built on trust and commonality…
God help the elites if the population finally meets at “the middle” someday. The power hungry need to keep us all angry and fractured to keep this crazy train on the tracks a little longer….so choo choo, all aboard the crazy train…
Weirdest Centrally Planned Economy Ever…
tax revolt is coming…..that is the end game…..no way they can corner it if done as movement….en masse…..
If they give a cent off to these twits with student loans in liberal arts, civil war 50%
reperations 100%