But it still won’t cover the dollar’s actual loss of purchasing power.
By Wolf Richter for WOLF STREET.
Among the inflation data released today by the Bureau of Labor Statistics was the Consumer Price Index for All Urban Wage Earners and Clerical Workers (CPI-W), which is used to calculate the Cost of Living Adjustment (COLA) for Social Security benefits.
For August, the CPI-W jumped 5.8% year-over-year. In July, it had jumped by 6.0%, in June by 6.1%. The summer readings are the highest since July 2008, and before then, since 1990:
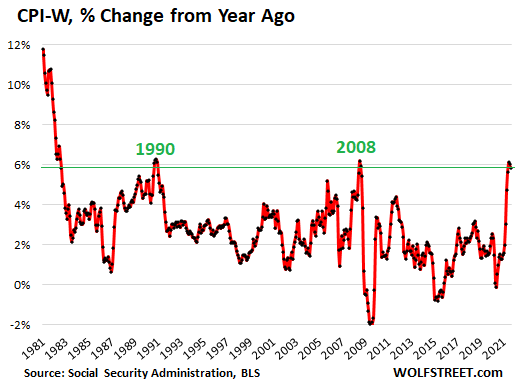
By comparison, the regular headline inflation number that was released today, CPI-U, rose by 5.3% year-over-year.
The COLA to be applied to Social Security benefits starting in January 2022 is based on the average year-over-year percentage increase of CPI-W in July (6.0%), August (5.8%), and September (to be released a month from now).
If the September reading comes in at 5.6%, the COLA for 2022 would be 5.8% (the average of July’s 6.0%, August’s 5.8%, and September’s 5.6%). This 5.8% would match the COLA of 2009. Both would be the highest since 1982 (7.4%).
When the September value of CPI-W is released in about a month, we can estimate with some accuracy what the COLA for 2022 will be (red = estimate based on actual July and August and September projection of 5.6%):
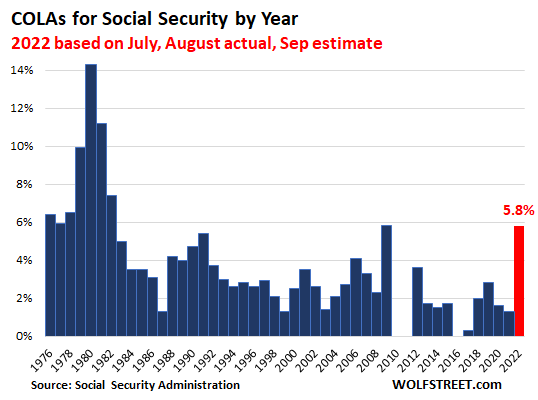
While this type of COLA will provide some relief from the price increases that have been gnawing away at fixed incomes, it will still be insufficient to compensate for the surging costs that individuals may face in housing and other major expenses, depending on their situation and location.
If the beneficiary rents in a city where rents have been soaring in the double digits, a 5.8% COLA won’t go far. If a beneficiary drives a lot, the 43% jump in gasoline prices is going to hurt. Used vehicle prices are up 32% from a year ago, new vehicle prices 7.6%.
Housing costs account for nearly one-third of the regular CPI. But the index for housing costs has been repressed by the method in which it is calculated. The index for rent rose only 2.1% and the index for the costs of homeownership rose only 2.6%, while home prices have soared at rates not seen in the decades for which we have data: 23% according to the National Association of Realtors, and 19% according to the Case-Shiller Index (I explain the disconnect in housing inflation and CPI with a stunning chart).
Then there are healthcare costs, which can be a major issue, despite all the parts of Medicare.
The COLA for 2021 was only 1.3%, which was based on the average of CPI-W in July, August, and September 2020, when CPI readings happened to be very low. So, given the price surges in 2021, that lousy 1.3% COLA this year is leaving many people deeply in the hole. And now, a lot of big expenditure categories have already outrun what might be a 5.8% COLA next year.
Inflation means the dollar loses purchasing power. And over time, COLAs will be purposefully insufficient to compensate beneficiaries for the actual loss of the purchasing power of the dollar as encountered in real life. If Social Security payments are the only source of income, actual inflation, as encountered in real life, will nearly guarantee a continual slow reduction in the standard of living.
For this reason, it’s important to have a nest egg with a combination of assets, and/or create or maintain an additional income stream for as long as possible, preferably something that is fun to do and keeps people active and engaged. Even a small-ish income stream helps out in a major way. Inflation, as encountered in real life, is the enemy of fixed incomes, even if those incomes are adjusted for inflation because those adjustments are likely insufficient to compensate for the actual loss of purchasing power of the dollar.
Enjoy reading WOLF STREET and want to support it? You can donate. I appreciate it immensely. Click on the mug to find out how:
![]()


Seniors used to have the option of a super safe cash “nest egg” in the banks as a CD/money market earning a decent interest rate to supplement their social security.
That is gone now. Stolen in the era of ZIRP.
Their own choice now is very risky “investments” that pay some kind of yield.
“For this reason, it’s important to have a nest egg with a combination of assets, and/or create or maintain an additional income stream for as long as possible, preferably something that is fun to do and keeps people active and engaged. Even a small-ish income stream helps out in a major way. Inflation, as encountered in real life, is the enemy of fixed incomes, even if those incomes are adjusted for inflation because those adjustments are likely insufficient to compensate for the actual loss of purchasing power of the dollar.”
I just bought 2 CD’s in the last month. .3 % interest. (3/10 of one percent) . Why do I even bother? I think if I bought $100 of lottery tickets instead of a CD I would be better off.
To be honest my best “CDs” right now, other than some 3.1% “brokered (can sell at any time) 5 year CDs from 2.5 years ago. Funny enough, my 2% cash back credit cards (which lots of banks do now) are my best “CDs” as I put everything on them and pay them off every month,…go figure…
And I do get a kick out of moving money from Bank to brokerage to another bank to another brokerage…and for some reason they pay thousands to do this, and you only have to leave it at one spot for 3 to 6 months. I guess you could say I love playing “bank” with the banks…HA
Those cashback credit cards make inflation worse. They are not giving you anything. The merchants are paying them a fee which is split between the credit card company and you. And you (and we) are paying for all of it through higher prices. If you paid cash for more items, all of us would have lower prices.
Wells Fargo is currently paying me $700 to hold $50K for 3 months. I’m constantly looking for these options.
the newly retired will soon find out
that over 50% retirees live in POVERTY
for nearly 10 years now govt keeps stealing income via NO INTEREST
and retirees have to drain their bank accounts
over 50% have less than $10k cash(many none)
spoke with sister who was state worker – turned 65 and now has to go on SSI from disability – $400 a month less
and she pays $40 co-pay 3 times week sucking them dry
merika – newest 3rd world country – going way of mexico and so many other countries
Globalization brings 3rd world prices of labor and goods, but also standard of living. The sooner we deglobalize, the better. World government by the rich global elites will be serfdom for the average people.
@Petunia:
The cash back credit cards likely have no impact as you are not paying more than you would if it were a regular credit card, a debit card, cash, EBT, a “points card”, or whatever. The “vig” is already baked into the prices.
For those who are retirees, you might look at your local grocery store’s website to see if they have a “senior day”. Here in PHX, Safeway and Fry’s Foods offer theirs on the first Wednesday of every month. They offer a 10% discount on pretty much everything but booze and pharmacy. We do the bulk of our shopping once a month for staples and stuff that keeps / freezes. Do a touch up two weeks after to fill in perishables / fresh.
If you use geezer day plus their “reward card” and app, you’ll find that you can often get a discount of 40% or more from what you would pay if you just walked in cold off the street.
El K: Thanks for clearing that up. There are couple repair business I use which offer cash discounts up front. My supermarket lists manu rebates on their member website. Often times the rebates coincide with store sales. Then the store comps me with bottom line coupons, no restrictions. The rebate money deposits directly to your paypal account in a few days. I also get a 10% military discount at Lowes and put the purchase on my CC for cashback, and pay the balance each month. Lots of ways to save, just takes a little time and effort.
To add insult to injury the interest is taxed. We live in ridiculous times.
The double insult to injury is interest is taxed at higher income tax percentages than the lower capital gains tax percentages for various “Capital gains”…so it would seem that cash is not considered “Capital” by our govt???
Basically the govt rewards speculation and penalizes safer capital investments…surreal…
you do know you can get .4% for a high yield savings account at American Express or TIAA Bank and your funds are not tied up.
Rental property is a great earner, also inflation protected for the most part. Like anything else, timing is everything.
Lol, depends who you rent too and if there is a pandemic. Having leverage as an geriatric individual is prolly not the best play
Careful !
You will wake up georgist.
Wasn’t Keynes that talked about how the government could steal a citizens money through inflation without 1 in a 1000 figuring it out. The BLS method of calculating housing cost fall into that category. All you have to do is plot real rent vs their method for 30 years and you can see that their method is BS.
You probably bother because when you get older you need stability in a portfolio. You can’t risk a 60% drawdown while taking out 4 – 5% per year.
Blue collar workers used to have the option to work in factories for good wages and benefits.
That’s all gone now; exported to other countries.
Stolen by greedy businessmen.
Did you protest that ?
No ???
The powers that be came for your high earning CDs.
It’s your turn now.
I actually did. I’ve opposed free trade and all unskilled immigration for the past 20 years (when I was only 19).
I thought NAFTA was the dumbest thing ever signed. It was an in your face betrayal of the working class, by the dems. Never voted for them again.
When I worked for an auto manufacturer who had plants in Mexico, the humorous anecdote of the day was how many things were stolen off the cars as they made their way from the Mexican plant to the U.S..
Batteries, tires, seats, engine parts – despite the armed guards on the trains, fully enclosed rail cars, dedicated rail spurs, a Mexican government guarantees . Then there was the issue of people who camped in the cars….. and left their trash and you-know-what in the interior (no bathroom in the rail car). Every time the gringos would implement a “counter measure”, the the thieves would bypass it in about 2 seconds.
You can’t forget the “rework” buildings at the port of entry. Body work for dents as they walked over the cars, repair bullet holes, parts replacement, general repairs to shoddy assembly. Then there were the cars that were crushed because they simply were beyond repair.
Never figured out how that penciled….
Petunia, as was the 1965 Immigration Act. Both destroyed the middle class and by extension, America.
@ Petunia
But NAFTA was signed in 1992 & negotiations entered into long before that; Bush was the President so I’m not sure what you’re talking about. This arrangement had nothing to do with political affiliation.
MarkinSF,
The left likes to blame NAFTA on the republicans because the reps wanted it for their big donors. At least the reps own their support for big business.
The dems were the ones who actually passed it while lying to labor about its impact, and hiding their support for big business donors too.
So technically you are right that labor got screw by both sides. But one side owns it, and the other is still pretending they had nothing to do with it.
@ Petunia
On the other hand the Repubs pretend to be a friend to the common man. Which is absurd on the face of it. Politicians will be politicians and pretending that somehow the Republican party and their politicians are honest brokers is just a wishful fantasy. The reality is that financial capitalism is an animal that will ultimately eat its own – after it’s finished with you and me.
I also opposed how unions where for only government workers and they get higher wages, benefits, sick days etc. for decades now and back stabbed private sector workers. I lost my full time manufacturing job back in the mid 90’s making $800 a week net pay after free trade came in and now work usually stable, 2 part-time, contract jobs. I have been mostly doing shipping and delivery jobs for local warehouses, stores and some regionally, out of the city, towns.
I did keep track on my spreadsheets my average weekly net pay since 1997 and it is $625 a week. I am currently earning $760 net pay weekly on average but I am also working 50 to 55 hour weeks.
I did manage to save quite a bit of money, $650,000 in my IRA’s, CD’s, savings accounts, I-Bonds over the years, 25 years to be exact. My nest egg is mostly locked in longer term CD’s, IRA’s, 85% of it which is not doing too bad earning average 3% and don’t mature until 2026 to 2029. I rent a modest apartment,$1,400 a month+utilities, single and have no kids but after all my expenses still have $250 to $275 a week left over. Now being 50 years old I am glad I did not blow it all on stupid stuff.
Fun and engaging activity which creates income stream are apartment rentals, which is very expensive at this moment where rents are not even paying the monthly mortgage. Or it has been disastrous past couple years.
Willing to hear couple other examples ,to have an idea of creating my own retirement, since I don’t want to relay on SSI in my retirement age, please?
Simple to say/describe, not so simple to do ebpm:
1. Pay off all debt, including ”mortgage” first.
2. Find RE with good neighbors ( whose politics you are at least OK, if not agree with,) with reliable spring or solar pumped well or rain, and fertile soil. Perhaps go so far as to surround yourself with food and energy self sufficient folks.
3. Cultivate long term ”food trees” and build up soil health for garden, etc.
4. Vote against each and every rise of local taxes, knowing full well you cannot control federal taxes.
5. Cultivate knowledge of and practical experience with energy self sufficiency technology and build or remodel shelter to provide greenhouse, natural ventilation, natural cold storage of foods, etc., while utilizing solar, wind, and gravity (hydro) sources of electricity until they don’t work or work enough…
Forget about any certainty of any ”financial” investment, etc.
“Pay off all debt including mortgage first”.
I tend to agree with this, but I am beginning to wonder. For 12 years the Fed has rewarded maximizing debt to buy nearly any asset. If you are 35 or younger you don’t know anything else.
It is a matter of timing, Poor Millennial. Now is not the time for us average Americans to acquire rental properties and expect a positive cash flow. We must wait. We must wait like tigers wait for the right time to pounce… and that time will come. I’ve had my time and I may not be around when it does come again, but you will. While waiting for that “right time”, one can prepare for that time by defining what you need to do in order to pounce… (a strategy, so to speak). For me, this would be to “Increase Cash Flow and Net Worth”. This can be accomplished by: a) Decrease recurring expenses, b) Increase recurring income and c) Create new sources of income. In other words, Amplify the money coming in while lowering the money going out. Also, it sometimes requires looking at things a little differently than we have in the past. Case in point: if one considers refinancing a mortgage for the lower interest rate but the closing costs seem too high, one needs to look at the fundamentals. For example: the new mortgage with the lower interest rate will cost five thousand dollars in closing costs, but the new payment will save $200 per month. This means the upfront annual return on the 5 thousand dollars (re-fi cost) is $2400.00! Nearly 50% return… and that return goes into savings…. preparing for that time to “pounce”. There are other “sources”.. insurance costs is one where I found significant monthly savings achieved thru shopping and bundling policies. Even small, seemingly insignificant expenses add up. For example, that weekly restaurant lunch I treated myself to was halted during the depth of the pandemic… It was then I discovered the $20 bills I had in my money clip had stayed there. And no ATM trips to fill that money clip were required. And after one year… just 52 weeks of skipping that $20 lunch, I had saved $1,040.00. And I don’t mean you need to be a “Scrooge” with your funds, but don’t be foolish either. I used the “lunch savings” money to buy my granddaughter a MacBook-Air which she needed when she left for college. I got more pleasure out of providing that for her than any lunch I have ever eaten or any investment I ever purchased. I guess what I am saying to you, it is this: It is about the Benjamins and making plans and executing the plans… BUT living is what it is really all about… find and keep that balance. Good luck, Poor Milelennial, I hope my ramblings may have been of some benefit to you.
If you feel sad about that, think about how the Chinese investors that bought “real estate” from Evergrande Real Estate Group because the CCP-controlled, Chinese stockmarkets are so corrupt now feel. They will get nothing.
Then one ray of light in this is that the bankster Benedict Arnolds, who invested in Evergrande, are about to get a share of the same zero. LOL. The old “TANJ” saying “there ain’t no justice” apparently has a corollary: “there is justice on rare occasions”
Dare we hope that the millions affected will start to lynch the utterly corrupt, CCP members? Will Christmas come early this year? LOL. Keep your eyes on China for a while and get some popcorn ready.
I forgot to add: you have got to love the Evergrande financial managers; they are true commies. They cannot afford to pay their employees even, who are protesting. They cannot afford to pay their suppliers or finish their hundreds of projects for which they were paid huge down payments in advance. They cannot afford even to pay what they owe their CCP banks OR EVEN INTEREST on those loans! Yet, they say that bankruptcy is out of the question!
Evergrande commies, you are already bankrupt! You just have not filed the papers yet because the massive numbers of police have been keeping your creditors from stringing you up. They are like the captain of a ship hit by a torpedo in WWII, who is rumored to have said: “but it is just a little hole” as his ship was sinking, and the sharks were swarming nearby.
The Feds will boost Medicare Part B monthly fee. They always do. Lets see what the actual increase is net of the increased Part B deduction.
Any guesses? 4.0%, 4.5%, 5.0%
Medicare Part B costs will increase by about 6% next year, according to estimates in a Congressional Research Service (CRS) report.
Whatever they give you through ss cola will be taken away by medicare. Medicare income limits will also take your 401K money.
They don’t really “take your 401K money”, they simply increase the premium once you exceed a certain income level (IMRAA). The current threshold is $88K for individuals and $176K for married couples. That is taken out of your SSI check (Part B. Part D is taken from your bank account.)
As you exceed every threshold, the cost increases about 50% over the previous level and hits both Part B and D.
Anyone who thinks Medicare is inexpensive and an answer to your health insurance dilemma, needs to look into the costs. Ours is somewhere around $700+ a month for the two of us (B, D, and supplement)…. or $8,400+ a year – if we don’t use it. If one of you is heavily reliant on pharma, you can fall into the “donut hole” where it gets interesting fast. And we’re still in “tier 1″…… This year we’ve paid out an additional $7K for “non-covered” expenses.
With a sick wife on a dozen prescriptions, two are Tier III, our OOP for meds is about $4k anually. Then the Medicare, Part D and supplemental insurance premiums add $8K per year. Plus, she is on O2 100% of the time and her portable unit cost us $3K (one time purchase), which Medicare didn’t cover.
Yeah, Medicare is a good deal overall, but can be costly if you want to choose your own doctors and not have any (or few) deductibles.
EL Katz,
If you are paying $7K for non covered expenses anyway, why pay the extra premiums for the “better” plan? If you just had part B, would it be $15K extra a year in expenses, unlikely.
Of all the stats Wolf presents this is the most telling (yet simple) reality that just amazes when you retire. I retired 4 years ago. Last year Medicare when up more than the “increase.” leaving for a 0 net increase in reality. Since last year and a half it has been like a high altitude jet losing altitude at a dizzying speed…. I have quickly reacted and more to come.
What is most concerning is thinking of the immediate and near term financial implications (which are not clear at all except for inflation).
I fear for those who have invested wisely in seeking shelter in a storm that is going to be long, unrelenting, and brutal at best…..yet no one really wants to “speak it” because they hope not for themselves.
Yes. Some inflation might get cudgeled, however, at least as to the US dollar, if what is happening to Evergrande, etc., causes systemic, economic shocks which reduce Chinese demand and cause them to desperately lower prices, or depreciate the Yuan again, to get dollars. A German, DW program even suggested that a coup that replaces Xi might occur.
I’m not taking any credit but did you read my comment on your last post? I totally called out CPI as only being there to control the COLA. I also asked you to produce the Wolfstreet index. CPI is a joke. Anyone who’s paying attention knows that real inflation has to be 15% at a minimum. I’d say it’s well north of 20%, though. If you’re on a fixed income (social security), you’re screwed. 20% real, 5.8% increase, that 14.2% difference may as well be a horribly regressive poor tax.
Make the Wolfstreet index
Shadowstats already has alternate inflation charts. As to Wolf creating an inflation index, that is A LOT of work, which Wolf does not need, since keeping track of the goods in the various inflation measures used over years in 50 states is not easy nor quick. Instead of presenting economic trends, this website would become primarily an inflation report. LOL
Shadowstats is a joke. He exaggerates by a huge margin. He penned in 11% and 12% inflation for years, when there was little inflation, meaning that the cost of living doubles every 6 years during that time, and that’s just nuts for the overall US population. Shadowstats gives alternate inflation measures a bad name.
My measure would be something in between CPI and Shadowstats, but closer to CPI than Shadowstats
No shadowsats is not a joke.
CPI is the joke, which is why it is “changed”. And why working people are BROKE. Unless they have assets which inflate.
Most of what you buy (esp. big ticket items) has doubled (or more) in a decade or so. Tell me Wolf…do we get there with those CPI numbers?????? Or is it “hedonic adjustments???
I’ve been around longer than you. I’ve watched it happen real time. I’m quite familiar with several industries and fields. All of whom people NEED in large capacities, and the costs have EXPLODED while the gov lies and say there is low inflation. Compound math is a thing. It would solve a lot of problems if the average person actually understood it.
You should know better Wolf. People read your blog for good analysis. Maybe explain to them why they are working harder to fall further behind, despite getting “raises”.
I understood that the consumer CPI measurement was changed dramatically after the 1980s albeit there are so many CPIs now reportedly. Is there any more accurate consumer inflation computation out there because my own basket of monthly purchases has been getting more expensive at dramatically high rates?
Sure hope the CCP goes the way of the dinosaurs. Getting rid of worldwide inflationary pressures by their demise due to Evergrande, et al, would be like winning the lottery. LOL
I have a theory monthly n.s.a CPI for next month will come in no higher than 0.1%. Several important CPI adjustments depend heavily on next months print.
Maybe the cpi-w for September will be -10% and the cola will be 0.
Let’s see what the roulette wheel of cpi brings.
Petunia,
I have all this data on a spreadsheet, the CPI-W, the averages for July, August, and September of CPI-W for each year, and the actual COLAs going back to 1975. I checked back to 2000: The SSA has not played games with the COLA. It always matches the the 3-month average. And I expect that to continue.
However, CPI-U, CPI-W, and all the other alphabet soup indices are easily being played with by the BLS. Or Congress can decide to use a different inflation index, such a chained index, and if it does, you will hear me squeal about it.
Local bank offered 25 month CD at 3 percent so I jumped at it. That was 25 months ago. Paid $127 a month for what I deposited. If I let it roll over at today’s rate I’ll get $12.50 a month. The SS increase Mr. Blitzer projects will give me about $90 a month. Not many seniors will come out ahead in this economy.
The AARP use to hold great power back in the 80s and 90s. And now the AARP seems powerless to help seniors with ZIRP Fed madness…really shocking to me. At the very least, and for very little cost compared to multi-trillions bonanzas, they could give folks over 55 the chance to buy “Senior CDs” that pay “CPI interest” rates. So this coming year, seniors could make 5.8% on a 100% FDIC insured “CD govt bond”, and it could be limited to say $1 million maximum. The same sort of CD could be designed to help 1st time homeowners, college expenses, etc. Instead of just sending free money for everything, how about we make folks place some skin in the game with their own savings, and give them a safe 3-6% return via “Make America Great Again and/or Build Back Better” govt CD bonds. Call it whatever…
I really feel the seniors got hit the hardest by ZIRP. I actually help pay my parents expenses as they can’t survive of SS, and their CD’s pay only 0.5% are not enough versus the 3-5% CDs of recent history. It is not right as they played by the rules, and then the rules got obliviated when it was their time to relax and not work 24/7…
The Fed is cruel as hell to both seniors and the working poor. Only an un-elected, personally super wealthy, Fed elitist cartel could retain such power as they would never get re-elected if we had a true democracy that did not protect the elites at all costs to the detriment of the bottom 90% of society…
Yort,
While certainly understanding the plight of your parents, they also have to bear some responsibility for their own situation…
Since the 70s, people, such as your parents, have stood by idle as the financial sector has stolen and been given the individual equity of the citizens of this country without concerns for later…
Generally speaking, If you could jump on the way back machine and observe the financial decisions many of today’s seniors made before they became today’s seniors, you would probably not feel so bad for them and may even say “what the hell were you thinking?”…emotional connection for you is tough and I get it, but you have to lay the blame where it falls…
At the other end of the spectrum, many of today’s seniors are not doing badly…
Currently the government in China is slapping down the billionaires in their financial sector who are getting too big for their pants. This is characterized as “communist totalitarianism” in the Wall Street backed MSM. In reality, it benefits the non-top 5% the most. No wonder the plutocrats fear it.
In book “Die Broke” author recommends when it becomes obvious your funds can’t support you for life, then to buy an annuity as at least you will have some guaranteed income if you happen to live to an old age.
My cousin sold my uncle a life annuity for his pension transfer to an IRA and gets $3,000 a month with no annual inflation increase or annual increase of any kind.
The amount was on a $515,000 policy. This was back in April- 2010 when long term 30 year US treasury bonds were in the 4.5% to 4.6% or so. Now, looking back a guaranteed for life of $36,000 annual payout is 6.99% on $515,000.
It looks good at the time but I personally see that a 4.5% US treasury bond pays $23,175 a year interest and he still has his $515,000. The difference is only $12,825 a year more payout but when he dies, there is no more $515,000 principal.
He would have to live 40.15 years just to get his principal paid back or $12,825/$515,000. Unless he lives to 2050, the insurance company made out good on this life annuity.
OS – unfortunately the $500 a month check from your annuity will only purchase one Big Mac, a large fries and a small shake. But you’ll eat “well” one day a month.
AARP became involved in politics unrelated to retirees a while back. That’s when we dropped our membership.
AARP is now not much more than a marketing arm. Witness “AARP Medicare Drug Coverage” offered by United Healthcare.
AARP began as an insurance agency. It still is.
Almost 90 percent support allowing Medicare to negotiate lower drug prices based on the prices that other countries pay (way lower), per a Kaiser Family Foundation poll earlier this year. Yet just today three Team Blue members killed this part of the $3.5 trillion bill in committee. So basically the drug companies bribed these three blue members with so much money, this cost savings was not even allowed to get to Congress to discuss or vote nay or yay.
So yes, AARP seems to be a joke as this is low hanging fruit with a near 90% voter approval rating…surreal…
US Treasury I-bonds will get you CPI rates, but you can only purchase $10K to $15K per year maximum, depending on your tax circumstances. You can by $15K per year if you are owed that much in income tax refunds, otherwise $10K per year.
Let’s say the COLA is offset (zero su) by the Medicare Premium increases. The net effects is a higher AGI which affects marginal tax rate and the possibility of higher Medicare premium due to IRMAA (2 years after the COLA increase)
https://secure.ssa.gov/poms.nsf/lnx/0601101035
The charade that has been the federal budget and solvency is drawing to a close. The artificially low inflation rate (check out John William’s Shadow Stats) was helping keep things somewhat under control. These higher COLAs will drive the debt up even further in addition to all the other craziness going on.
Unless the Social Security (FICA) taxes on wage income rise faster than CPI, the ramping COLAs will make the Social Security “trust fund” evaporate sooner. Wonder how the math on that pencils out?
It’s possible Federal solvency might actually be saved by Federal Reserve balance sheet engorgement. If inflation boosts tax revenue but the net debt (that owed outside the Federal Reserve) doesn’t increase, AND if rates stay low, then FedGov solvency improves. At the expense of everyone on the wrong side of the inflation.
Back of the envelop would pencil out to social security running out of funds in 2029 instead of 2034 if we have 8 years like this one. Fed policy isn’t free.
Using the price of a new home as an inflation indicator, the CPI under reported housing inflation much of the time.
The MSRP for a new vehicle seems reasonable, but there none available for that price on some lots.
According to one study, 40% of retirees relied on Social Security for 90% or more of their retirement income. Other studies varied.
Dividend yields are lower than in times past. The one year CD yield for a $1000 deposit is .7%. The current administration wants to collect more corporate taxes potentially lowering stock market returns.
Note to Jerome Powell
For every action, there is an equal and opposite reaction.
Whoever is whispering in your ear, giving you modern monetary theory tid bits, is misleading you.
And now, per the MMT …. to calm inflation comes the tax increases…stealing from the private sector and putting it in the hands of politicians and their vote buying schemes.
The question is what is going to happen.
COLA is what it is – but inflation expectations are a different story.
Wage-price spirals are precisely the classic stagflation story.
Are we in for another era of Disco?
“Stayin’ aliiiiiii,iiiiiiii,iiiiiii,iiiiiive”
The election in California shows that we’re way too far gone for anything to change without a full collapse.
IMO, the California results were as predicted. That is really not important. What is important was the battle, and the method used by both sides. The recall group fought on the basis of ideas, and the bad results of the present administration’s edicts. The anti-recall group sang platitudes and spend hundreds of millions to keep Newsome in office.
Personally, I am glad Larry Elder did not win. California is sliding downhill very fast. I know, I lived there for 50 years and just left this spring.
The forests have been mismanaged, the roads are deteriorating, businesses’ have left the state in droves, homeless are everywhere, the urban areas are dirtier than ever, rolling blackouts are more common, taxes and regulations keep going up, it is too expensive to live there for the middle class people…I could go on and on, but you get the idea.
The last ten years there living in the San Fernando Valley were terrible. Even the people (neighbors) are nastier.
Californians have never met a tax increase, or added business regulation the didn’t like. They voted AOC’s dictum – TAX THE RICH.
That’s what you get by living in a one party controlled state.
If Newsome were voted out, and Elder elected, Elder would have been blamed for all of California’s woes and his free market policies would have taken a beating by the mainstream media.
THE STATE IS GOOD, THE STATE IS GREAT – TAX THE RICH. YAY SOCIALISM IDEAS. That should be the state motto of California.
RightNYer, I hope that you will join me in hoping that the “full collapse” will be peaceful and not result in any violence. The time for hate must be supplanted by tolerance and good-will.
William Susel, I do agree with you on that point. I would rather let the Dems run hog wild and destroy everything so people know who to blame. But my point is that the third worldization of California has led it to that one party state.
I also do hope that the collapse will result in a peaceable dissolution of the United States into two nations. But to quote Jefferson:
“Peace and friendship with all mankind is our wisest policy; and I wish we may be permitted to pursue them. But the temper and the folly of our enemies may not leave this in our choice.”
Petunia, nothing will change without economic collapse. That’s when the battle lines will be drawn.
We are too far gone, I agree with your comment about Japan and this one too.
I agree! Collapse here we come! I believe the fed wants one. All of their buddies are salivating for assets at 10 cents on the dollar!
Once they went to untethered fiat it was inevitable that the end would be too much debt and negative real rates. Die was cast 50 years ago. We are going to be Japan or we are going to reset imho
We’re not going to be Japan. Japan is a virtuous, well ordered, homogenous society with good values and a trade surplus. We’re none of the above.
The Fed has created a situation, an environment in which
1. Stocks and assets may decline in price
2. But if you are in cash, you lose to inflation
if they fight inflation with interest hikes, it may cure pt #2 at the expense of pt #1
if they dont the damage to all those not fully invested will be catastrophic….amplifying pt #2 which will eventually hurts stocks and assets.
The Fed went off the rails and cant find the tracks
If the FED stops supporting the stock market (directly/indirectly), then game over.
How can they STOP Supporting the stock market when they are investing in it ? They are driveing the market & I doubt they well stop unless they pull their Funds first :
Game over is for the rest of the Public
The impact of the ZIRP/QE approach (on its way since ~1985), is that the old way of providing safe returns via savings vehicles- bank accounts, CDs, etc., is gone. Some call it “stealing” savings- which may be right.
If one wants a better (any meaningful?) return, one has to take more risk.
How this gets resolved is the big question.
As far as the retired/older population, the difference between now and say ~60+ years ago is that population is now RICHER than they were due to social security and medicare. The younger generations are actually relatively poorer than they were ~60+ years ago.
I hear your point, but it’s somewhat of a misnomer that ZIRP/QE suppresses yields even for safe investments. It suppresses yields for ALL investments. Traditionally, companies that needed to raise money through “junk bonds” had to pay huge premiums to borrow. Now they don’t. So even “unsafe” investments have no meaningful returns.
WK…W,
I dunno… I was pretty poor then… 60s…
Younger generations are probably net poorer than we were then… today’s poor are at the end of a long inflation cycle and there are a whole lot more of them due to population increase… plus you see them more now…
But offsetting that is the anti-poverty initiatives (read giveaways) that many of these people could have used to escape poverty but didn’t… although many did…
Poor is seldom one generation… typically multi generational clusters…
Also to add, that yes, a lot of younger people (non poverty types 45 and below ) are indeed poorer today than yesterday but why wouldn’t they be… they haven’t been around long enough to gather assets and struggle over many years…
Add in the casino memes of investing, overpaying for nearly everything, YOLO, experiences instead of substance and the general I deserve a great life because I’m ,,, well,,, alive…
They are after all, the boomers kids….
Who do you think is buying all the overpriced houses cars, stocks, and boats…
What a terrific article. Informative and cautionary, both.
One issue I have was in the last paragraph:
‘Inflation, as encountered in real life, is the enemy of fixed incomes, even if those incomes are adjusted for inflation because those adjustments are likely insufficient to compensate for the actual loss of purchasing power of the dollar.’
I would change ‘fixed incomes’ to ‘all incomes’. Now that union membership has been demonised down to single digits in the private sector, most employees have absolutely no way to negotiate their pay rates with employers, including any pension they may or most likely will not have. Sure, there is a temporary blip with the current worker shortage, but that won’t last. This has softened up an entire generation of people who are now seniors and reliant on SS.
You can bet those implementing the COLA adjustment for SS, and those who influence economic trends with their power most likely have a pretty good income stream beyond the average Govt pension.
Wolf’s point about having a side interest for extra income was an excellent idea. Another aspect to this is an interest in preparing to live a life, a rich and rewarding life, but with reduced expectations of consuming. This might include preemptive downsizing, sensible relocation, learning to cook and reduce dining out, gardening, or reducing driving and travel for travel’s sake. I’m not sure Govt retirement income was ever meant to be anything beyond the basics. I have a friend who was crunching his numbers with me a few years ago. To my horror he had added in both his wife’s and his own meagre Canadian pension stipend into each others, in short he doubled the amount for both by adding them up twice. When I pointed this out he would not believe me.
The Canadian Govt pension plan is far lower than SS. It was designed to provide just 1/3 of pre retirement income. At 65 there is also ‘Old Age Security’ an extra $650 per month added on the the Canadian Pension Plan. If you don’t have paid for housing or another income stream, and live on your own, it will be tough to survive. Of course medical costs are not an issue.
Yort, I commend you for helping your parents out. We have just finished that aspect of our lives, not with money, but with driving for medical appointments, stay overs to combat isolation, repairs and maintenance on home, helping with mental decline, etc etc etc…..all the way to final days during a pandemic with no hospital visitation. Aging is not for the faint of heart, is it?
Paulo,
Your comment is a little confusing when you refer to govt pension income. In the US it can be either a pension earned as a govt worker or SS, or both. I assume you mean an SS type pension.
I was speaking to someone recently who is a US govt employee. Many workers are taking retirement and they can qualify for both the fed pension and a partial ss pension. These workers may also work another job in retirement. This is also true of most local and state govt employees.
I’ve seen many of these retirees over the years, they are among the most well off people I’ve seen. They tend to buy expensive houses and accept lower wages because they can. As the number of retirees grows, I expect these distortions to increase.
Enrollment in the defined benefit US Govt pension system (CSRS) was discontinued in 1985 and replaced by the FERS system which is a defined contribution system. The new FERS system does have a SS component (the old CSRS does not).
The end result is that FERS pays a federal employee retiree a lot less retirement benefits than the old CSRS. Also since the FERS is portable, most young people now use the US Govt as their first employment “stepping stone” and typically leave after a few years for a better paying private sector position.
Since modern central bankers believe they can print savings it was inevitable that savers would be the losers in modern central banking. As long as rates are zero and stocks are at 99% percentile valuations I will slowly transfer longer term savings from fiat to precious metals.
Inflation can be fixed by owner-equivalent grocery shopping, minus chicken, pork, and beef of course.
You”ll have nothing and be happy.
That bar graph indicates to me that the last time the feds provided accurate inflation statistics was under Jimmy Carter in the late ’70s.
6% inflation = 6% savings rate. You work hard, manage to save 6% of your income, then the Federal Reserve takes it from you.
If you want to tax wealth, tax wealth, not middle class savers.
I have news for you. Going all the way back to the 1980’s, the elites already knew the wealth of the country was in the middle class. Yes, the laziest, most unproductive workers on the planet were also the richest.
Getting the picture yet…NAFTA, World Trade Organization, Favorite Nation Status, over regulated small businesses, unregulated immigration…
Petunia- bingo.
“Getting the picture yet…NAFTA, World Trade Organization, Favorite Nation Status, over regulated small businesses, unregulated immigration…”
Some increased level of globalization of the economy was/is inevitable and desirable. However, when there is obvious predatory activity, e.g. driving down wages by driving down safety, environmental, health and other costs outside the country is obviously not “competitive free enterprise”. It is a subsidy for firms and people able to shift/globalize those costs.
Local labor market participants can’t “globalize”. Those people compete against the global labor market via immigrants and off-shoring of business activity.
Fed has made a bleak future. Long term reality was you could get keep up with inflation in t-bills and make about 3% over inflation in long term treasury and about 6% over inflation in equities. Now it’s -5% in t-bills, -4% in long term treasury and zero in equities. Good job with the fiat.
Until we get campaign finance reform………what shocks me are the Medicare part B premiums. I had no idea they were so high. I wonder what proportion of the GNP healthcare will have to be for some sort of action from our lobbyist/politicians…. 25%……40%…….60%……who knows? But something cannot increase forever. Every migrant we take triggers 12,000 per year in health care costs on Medicaid. Every migrant child triggers 28,000 per year in school costs. They would do better sending 1000 per month to every person in poverty on earth. On their own they could get a good bit more for their money than US healthcare. I assume the dems are shooting for population replacement. If you don’t think the electorate suits you just replace it.
I do think that the only cure for the massive corruption in all levels of US government is now campaign finance reform, horrifically, severe punishments for officials’ corrupt practices (like bribe-forfeiture), plus massive estate, gift, and generation skipping tax increases to trim down the gigantic fortunes of trillionaire families and ordinary billionaires that purchased most of our politicians– hopefully concurrently also in the EU to avoid capital flight. However, on behalf of migrants, might I point out the situation in Japan.
Their economy is in deep guano even though I, for one, would trust the quality of most of their electronic products (except for Sony products, after my poorly made, Sony laptop rapidly burned out) over the products of any other country. Aside from their population decline, and nuclear accident(s), Japan should have a shining future as a near-superpower.
Why? Their population is under deep pressure and declining, because the majority of Japanese are forced to live in an oppressive, economically challenging, work and economic culture. Most effectively work for the pleasure and enrichment of their elites, not their own. (That is similar to, but not as bad as, the way Americans are being treated by US banksters.)
Migrants with sufficient skills, which can only be acquired with adequate schooling, enough protein when young, and adequate, lifetime nutrition, might have kept Japan’s economy growing. Now, since things will not change, if Taiwan falls, and the Wall Streeters keep shipping US capital to the CCP (now via stock indexes and mutual funds holding CCP VIEs and “real” CCP-Ponzi stocks) Japan might someday become China’s Cuba or Puerto Rico: a hopeless, depressing society living next to or conquered by, an oppressive superpower.
The same threats face us. If those same things happen, and the US population has not grown enough (e.g., due to blocks on migration) or has lost more of its skills due to our low quality educational system or worst performing and most expensive health care system-scam among developed nations, in twenty years, unless the CCP has finally been taken down by Chinese partisans despite their Orwellian surveillance state, BETTER LEARN MANDARIN, or at least, Cantonese.
Who was it who said during a war, words to the effect, “in the trenches, men of all colors and creeds, we are all brothers.”
RH,
Almost everything below the first paragraph is totally utterly ridiculously nuts.
Which part? I did go a little too Kumbaya there, admittedly. Having handled immigration, I do feel considerable sympathy for people who have been blamed, but have not been responsible, for the loss of good US jobs, which actually were shifted to factories in other countries.
Much amounts to a summary of various studies and media with similar positions: just one is “Population decline: A coming global crisis” in Asiatimes. See “Japan’s population is shrinking: What does it mean for the economy?” in world economic forum.
The US population is not shrinking like that, so it has better prospects, if what just happened in Texas and Louisiana does not keep happening regularly and does not get worse. See also “How does nutrition affect the developing brain?” in zero to three as to protein needs of children. See “U.S. Healthcare: Most Expensive and Worst Performing” in The Atlantic.
Unlike you, I have never been to Japan but was told how poorer, ordinary people in Japanese cities live in tiny apartments, apparently are oppressed by dominating bosses (at least by my standards) and work incredibly long hours, etc.
Admittedly, Japan will never actually be like Cuba, since it is much, much wealthier and even with its decreasing population, much more advanced, much more highly educated, and much more productive. Moreover, most news media reports on the CCP’s plans, etc., sound like they came from the plot of a Tom Clancy novel.
Japan reportedly is now allowing more migration, and arming somewhat against China’s PLA, so that trend may end. See “Japan warns US a ‘Pearl Harbor’ style attack from China and Russia could happen” in American military news. See “China’s Master Plan to Crush Japan in Battle” in the national interest.
However, while they may not succeed now, when even Australia will have advanced, nuclear submarines, China under the CCP does seem to want to dramatically increase its population with its three-child policy, develop, arm, and replace the US as the world’s hegemon. See “China reveals plan to become world’s biggest superpower within 30 years” in the UK’s independent.
This is legalized theft. of people’s wealth. I heard a financial talk show host imply that people who were savers were dumb and they needed to get into the casino. At least during the Carter years you could get a decent return on your liquid assets, even as inflation was out of control. Now you got the inflation but no interest on your savings. LOSE, LOSE
Swampy,
Give it time, my friend…
I, like you, have cut to the bone and still live pretty well…
When all this blows up, I think prudent, frugal people today will have their pick of the leftovers tomorrow…
And I think there will be some pretty good pickings…
SC, I wonder what this TS clown will be saying when the markets have some “revert to the mean” event and these casino players get their heads handed to them. Even the pundits over at Wealthion at the end part of their weekly videos have been saying they’ve been keeping back from this market, it’s just to risky and over-priced. I’m with COWG, cut to the bone, wait for better times, and make the best of it till then. The only bright spot in this is that some I-bonds I bought in the early 2000’s have just reset to a 4.6 % interest rate. The only thing making me any real return on savings for now.
Isn’t it inevitable for the capitalist system to devour not only others’ assets but it’s own labor slaves which, after all is what we all are.
Another way to look at it is we are still quite a large plantation with a stratified labor up to monied classes continuously battling for power.
SS (Social Security) benefits were never intended to be the sole income source for the elderly. SS with other labor legislation passed during FDR tenure gave the common folk hope for the future during a time of great economic stress. SS was a contract between worker and employer that would be re-enforced for many decades to come by many good wage earning jobs and defined pension programs.
With the advent of new labor/employer battles during the 1970’s and forward, the “social security” of old age was put on the auction block. Exporting of so many good paying jobs along with long term benefits, crushing of organized labor contracts, and finally new global trade agreements putting business agreements ahead of labor gains put the cork in the “progressive” ideas for the commons as a whole.
It’s a whole new world out there!
Yes the retirees in America for the most part are taking it in the shorts. The worst part is that the newer generations are still trying to figure out what the “He(*) is happening!
In so many decades past there was always a somewhat “gentlemens’ agreement” between labor and capital as to what direction our economy would go. Somewhat.
That’s all gone.
The corporate part of our economic society reigns supreme; locally, regionally, nationally and globally. We can no longer expect any political party in the US to defend the commons or particulary labor.
Greed is dominant and “good”!
Everyone is now “marketable” not only for individuals own sake but really cast onto a global market whose maw engulfs all.
It’s gonna get real ugly soon.
If you are receiving SS, and are covered by either Medicare and or a defined medical pension plan you are rich. If not, good luck!
America is and always has been all about money. You can weave all the stories about “freedom”, “democracy”, etc…..but it’s always been about money.
That’s the “fog of domestic existence”.
Schoolchildren are no longer taught “home economics” per se in their early years. They are propagandized to death on how to be, “better consumers”. And Praise the Lord if they fail! They will get their reward in the next life!
The good side is that this country does have fairly free access to information on how to conserve money. But it is a road that few choose to go down.
Beware the Seven Deadly Sins; they are alive and well not only in all of us and operative in our society.
Our Congress/White House et all have literally destroyed that “ladder to the middle class”.
The FED is putting the nails in the coffin of same.
This from the “wisdom” of a 90 year old, born during the Great Depression, experienced a “free market” syndrome for some decades then was awoken with the realities of a greedy government (foreign and domestic), too much a complacent electorate, and reeking with corruption, but, thankfully following my own drummer am retired for almost three decades on SS plus a small defined benefits labor pension plus modest savings. My top annual earnings never exceeded $32,000. Try that today.
I’m rich.
It’s gonna get ugly!
It is a bad game and young people need to be taught how to play it. We are not all labor slaves. I’ve never for a second counted on SS being there for me when I retire in the 40’s. Though, I am worried that with Fed-promoted inflation as a tool to “save the economy”, my retirement goal is getting harder to reach. Maybe it won’t be as nice as I planned.
Never count on Uncle Sam.
Turtle
In keeping with your comments.
Let us now completely disband the military in its entirety.
We will save over $ 1.3 trillion aevery year.
Because we can’t count on Uncle Sam.
Right you are.
Mail delivery too.
I’d like to see some COLA on my savings account.
Can we get those interest rates up yet, Mr. Powell?
savings interest 5% below inflation…
never happened before….and no one seems to care….
THEFT.
Theft indeed.
But if they want to juice this economy to the point of destruction then I’ll buy some assets on the cheap.
I don’t know why they feel the need to play this game again.
It’s all just so demoralizing…. either you invest in what you know to be an epic bubble inflated on the worst fundamentals we’ve ever seen … or you earn nothing and possibly risk losing to inflation.
There is no way to comfortably invest with confidence.
I know, huh? I have a windfall from selling my side-business and neither cash nor stocks make me too comfortable right now.
Maybe we’ll just blow it on a swimming pool. Flushing it right down the drain for some summer comfort might be just the thing.
Swimming pool, if it increases your home value, might actually not be a bad investment. You generally won’t recover the full value of home improvements, but you’ll get something, and with inflation it might net positive in nominal terms.
On the other hand, some home improvements are really liabilities – swimming pools require fences/gates/liability insurance, and a fair amount of upkeep too…
A swimming pool is like a new RV. Never makes sense from a financial standpoint. But that doesn’t mean it’s not worth the enjoyment (for some, who know what they’re getting into).
What you said is reality and is the result of 25 years of bad Fed policy.
I knew years ago, pre-retirement by at least 2 decades, that Social Security would never provide enough income in retirement to support a life-style that let one actually enjoy their remaining years on Planet Earth. Since I had my own business for almost 30 years, I always contributed the maximum allowed amount each and every year to an S.E.P. or Self Employed Pension or IRA, and now I have at least an additional 60% of Social Security payments from it.
I was effectively a Giant Squirrel that put additionally aside at least as much money as in my S.E.P. so now I have available to me another 60% of S.S. payments. For argument purposes only, lets say I get $30k from S.S. every year and have another $36k from SEP mandated distributions and post-tax dollar personal savings. One can live reasonably well on this sum, meaning having enough dough to travel and try to bail out residents on the extensive coastlines of the country when Mother Nature blows and floods them.
The point being that the Third Rail of Politics, Social Security benefits, is an accident waiting to happen with a Broke Central Government. One way or the other, means testing via assets owned vs. income realized as in today’s system where some (35% to 70%) of my S.S. earnings are taxed a second time, the Charlatans in the Swamp are going to reduce after-tax S.S. benefits. It is not just the gross benefit that you have to consider, it is the actual cash you have in your pocket each year after you pay the IRS their legislated share of that benefit come tax time.
Social Security in the United States was always intended to be a Supplemental Income safety net for seniors who have retired, and not 100% of the income necessary to live upon during retirement. I have done away with new rides every three years, expensive vacations, living beyond my means via living quarters, and probably still have the same buck I ever earned. This is not high-horse preaching, but just a word or two of caution for those out there still in the land of the 2021 workforce.
In closing, we need to rid ourselves of the U.S. Federal Reserve. These rich-themselves elites care none about savers and retirees who must buy very risky assets to try to supplement their retirement incomes due to ZIRP. No interest worth speaking of from money markets and savings accounts is actually a theft of the use of Americans’ money without just compensation. Theft can take many forms. We need to get rid of this entity that will have so much egg on its collective face in the next several quarters, you will think you are looking at an IHOP menu. They have failed miserably with their Trickle-Down Monetary Policies and the end result is one of a failing economy and financial system.
We get rid of the Federal Reserve and all those careful plans you made for your retirement turn into nothing as the almighty buck is a pittance of what it was once worth, but its your fantasy.
XC, ever hear of Gold and Silver, the Anti-Dollar metals?? Have a pittance in securities, really just a play account. Get rid of the Fed.
I’m more of a Myrrh man, although I do have a Frankincense ETF in case the shit hits the fan.
Psssht, I just keep a rainbow-pooping cat animated GIF NFT on hand for emergencies.
David,
You can thank Reagan ( cue Fox News trumpets and flourishes) for the tax on your social security and for delaying the COLA from July to January… six months off COLA lost every year…if you voted for him, you can’t b*tch now… if you didn’t, let’s hope these people die soon…
All of the financial machinations today are a result of the Boomer bunch… They have been in stocks and houses all their lives… the weight they carry as a voting block will force the government to protect them and their assets… They had the money and they consumed…
It will not change until, as a voting block, they are reduced in size until they can’t sway politics…
Cow, I am a baby boomer, and to blame my generation for the majority of ills out there, get real. Divide and try to conquer, the American politics of today. I paid over $500k during my working years into Social Security and Medicare, and will see only a fraction of that money back before I expire. You sound like I should expire tomorrow for the good of the country.
Baby boomers, and the previous generation, especially, blaming people who have been dead for more than a decade? Not credible. In any given year the current ones in power can change the law(s).
Also, blaming “capitalism” for what is going on now is off base. We have corporatism that has captured the regulators. Globalizing the corporations has allowed this to happen. If not for that, the Fed wouldn’t count so much.
Also, remember, if you don’t like the growth/size of government, the biggest growth has not been at the federal level. It’s state and local- all your state and local pensions, especially.
California is leading the way again. Note that the state has a kind of 3 tier economy: rich=tech, entertainment, physicians, lawyers, etc., middle= almost all state and local employees, low= everybody else (the most people in poverty of any other state).
That’s what they have voted for…. again.
SEP IRA is the cat’s meow. $50K annual limit, more or less. Roth IRA is awesome but $6K limit? Come on, can’t defeat the SS problem w/that.
It’s hilarious all the games Uncle Sam plays with the tax code. This for Bobby because he has six kids and that for Sammy because he’s self-employed. Why all the picking and choosing?
I’d ditch the Fed in a second and in half a second I’d kill the IRS with a zero deductions flat tax rate. No retirement accounts.
K.I.S.S. The US became too complicated for its own good decades ago.
My advice for younger people is to try to end up with money in all types of accounts so you have flexibility to deal with ever changing tax code. Keep dividend payers in IRAs and non dividend payers in non IRA accounts.
Also, at market tops sell stocks in your IRA rather than your taxable account. At market bottoms, replenish your IRA with stocks.
Except that you need a crystal ball to know when the tops and bottoms are going to happen.
The variable between producer prices and consumer prices is corporate earnings (already under wage pressure) assumption being that consumer prices are a constant, while rental increases are sticky, (its like the Fed is taxing you for stock market inflation) and post eviction moratorium a lot of people are signing new leases. I consider the Apple product for instance something most users only access maybe 1/3 of the product, consumers pay for a lot for stuff they don’t use, much like cable TV. Should the company try to raise prices, workers in China cannot afford them anyway. If I was betting on corporate earnings, I wouldn’t.
If the monetary/debt system faults, what areas of support by the government/Fed will be prioritized? It seems the ‘weight’ on the shoulders of the system can be pushed on forever, but the constant redistribution/re-balancing of the ‘weight’ might cause a massive dislocation.
When are the damn interest rates on treasuries going up? Don’t give me that fractional percent/ few basis points BS! We all know what’s going on. Tired of the blatant lies!
The interest rates won’t be going up because it is artificially suppressed by FED.
Don’t wait on things which may not happen instead try to play the market.
You can’t control what FED does but can make money in the market if you can take risk. There is no price discovery in any asset class in any country in the world.
“When are the damn interest rates on treasuries going up?”
When doing so won’t have a highly negative effect on this:
Interest Expense on the Debt Outstanding for 2020: $522,767,299,265.34
In other words, never.
DawnsEarlyLight,
Right now, the Fed is still buying $120 a month in securities. The government has hit the debt ceiling and can only replace maturing securities but cannot issue new securities. This is putting a lot of downward pressure on yields.
When the debt ceiling is lifted, the government will issue lots of new securities, and this will happen at about the time that the Fed is tapering its purchases. So that’s when long-term yields would begin to rise, I think.
Good call, Wolf. The guys at the levers, like in the Wizard of Oz story, are mostly sound and fury, and when their manipulated system gets so humongous and complex, they literally do not know who is on first base. The Repo market spike in rates to 10% in late 2019 is a sterling case in point. Unintended consequences? Roaring inflation comes to mind. Rates are going up, first at the longer end of the curve due to excess supply (market values down, rates up), and then finally in 30 to 90-day Bills. The Wizards need permanent vacations.
If the government “defaults”, expect interest rates to immediately jump. How much they would jump is the only question.
I would think at least 150 to 200 basis points jump as the biggest increase in interest rates not seen since Greenspan during the US 1987 stock market crash. 10 year US treasuries would be 2.90% to 3.4% easily, 3.40% to 3.90% for 30 year US treasuries. If the default lingers on 5% to 6% US treasuries are really possible in comings moths, year.
That heavily manipulated CPI is still just way too high!
It looks like it’s time for an even more “accurate” way to calculate it which was the stated goal of the 1996 Boskin Commission with their report entitled “Toward a More Accurate Measure of the Cost of Living,” but they obviously didn’t do an adequate job.
As we all should know, while their study had a 50/50 chance of finding that the CPI calculations back then produced figures that were TOO LOW, in government studies about finance the actual definition of “more accurate” is “beneficial to the government.”
I wish that the dollar was treated like bitcoin because then I could deduct the dollar loss in purchasing power as an investment loss. But no, bitcoin is an investment and the dollar is a currency in the eyes of the IRS. What a clever system!
The amount of money printing by the Fed is getting out of hand. $120 billion per month is enough to buy about 1000 F-35s each month, or 8 aircraft carriers or about 10 months of global gold production. Month after month after month.
I imagine what the history books say about the US in 100 years. This what happened… they were shockingly foolish with money for a long, long time.
I am retired and wonder how anyone could talk about Social Security and Consumer Price Index (CPI) without mentioning Democratic Bill Clinton’s, Boskin Commission of 1996 where the formula for calculating the inflation rate for retired people was changed to minimize the inflation index for seniors on social security. Bill Clinton succeeded along with the Hoover Institute in lowering social security payments for all recipients over the last 25 years.
I don’t have an answer for the future. It is above my station in life
Jay,
Currently, SS is adjusted for inflation via the CPI-W. For August, CPI-W = 5.8% year-over-year. The regular CPI-U was 5.3% year-over-year. The COLA adjustment for SS benefits in 2022 is going to be around 5.8%. I don’t think the issue is the choice of CPI-W over CPI-U.
The issue is how the CPI complex is calculated, particularly with the distortions of housing costs and hedonic quality adjustments for durable goods.
https://wolfstreet.com/2021/09/14/social-security-cola-for-2022-to-be-near-5-8-could-match-2009-biggest-since-1982/
https://wolfstreet.com/2021/09/14/inflation-whac-a-mole-new-vehicle-prices-spike-as-used-vehicle-prices-dip-while-housing-inflation-which-exploded-in-reality-barely-budged-in-the-cpi/