Retailers willing to battle ecommerce will find “ample availability” – the shuttered stores dotting the sidewalks – and much lower but still very high rents.
By Wolf Richter for WOLF STREET.
The collapse of asking rents for vacant retail spaces lining the sidewalks along the 17 major shopping corridors in Manhattan has been spectacular. Since the beginning of the meltdown in 2015, the average asking rent in a number of these corridors has now plunged between 50% and 68%.
But there were a few exceptions. And in one corridor, retail rents soared 70% since 2015.
This is the first half of the seventh year of the meltdown. The whole brick-and-mortar retail model has come under question. Rents in Manhattan, even after the plunge, remain expensive, and retailers, already under attack from ecommerce, are having trouble surviving.
Over the past 12 months through this spring, asking rents fell in 16 of the 17 shopping corridors, according to the Real Estate Board of New York’s just released Manhattan Retail Report.
Landlords are trying to nail down potential tenants with hefty improvement allowances, such as free rent for some months, flexibility on renewal, and other incentives and inducements.
For retailers trying to set up shop, this scenario offers “ample availability” – the empty stores dotting the sidewalks – and lower leasing costs. But this may still not be enough to overcome the two-decade long structural change in how Americans shop, namely online.
So the hope is that if retailers that sell goods can’t make at those rents, or at any rents, maybe shops that sell services and are not being squeezed by ecommerce, such as hair salons, barbershops, yoga studios, dance studios, cafes, and dry-cleaners, might be able to make it.
Folks are now looking for green shoots in the retail sector, but if you look at the charts below of average asking rents per shopping corridor, the pandemic hasn’t visibly altered the meltdown in retail rents that is now in its seventh year.
Midtown
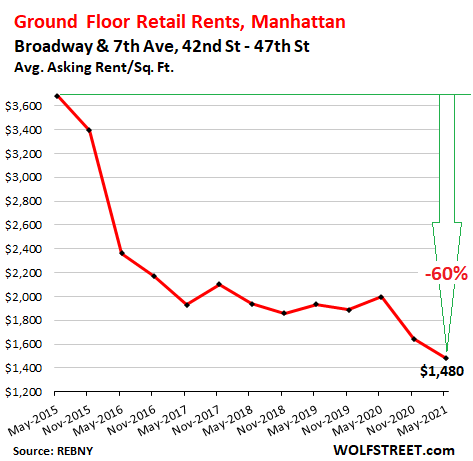
Some of the toniest shopping corridors are in Midtown. On Broadway and 7th Avenue, between 42nd Street and 47th Street, the average asking rent in the spring 2021 collapsed by 60% from the peak in 2015. Yet rent is still a mind-boggling $1,480 per square foot per year. For example, the rent of a 1,000-square-foot store would amount to nearly $1.5 million per year.
A global luxury retailer would treat that kind of store as a prestige showcase of its products, and would accept the losses from that store as a form of advertising expense, relying on its other stores to make money. But for lesser retailers, that equation doesn’t work.
Year-over-year, the average asking rent plunged 26%, with eight ground-floor retail spaces available for rent in the corridor:
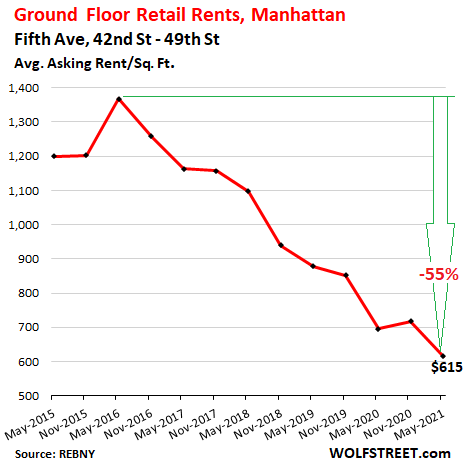
On Fifth Avenue, from 42nd Street to 49th Street, the average asking rent dropped by 11% year-over-year, and by 55% from the peak in 2016, to $615 per square foot per year, with 15 ground-floor retail spaces available:
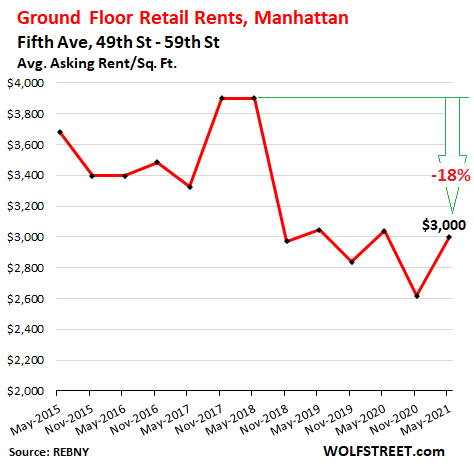
But on Fifth Avenue from 49th St. to 59th St., the average asking rent, on a year-over-year basis, ticked down only 1%, after a big jump this spring, to $3,000/sf, and was down 18% from 2015. That’s some serious rent: $3 million a year for a 1,000-sf store. There were 7 availabilities:
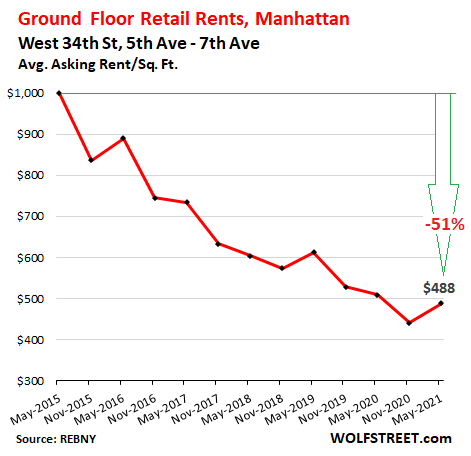
Midtown South.
On West 34th Street between Fifth Avenue and Seventh Avenue, the average asking rent ticked up this spring to $488/sf, but was still down 4% year-over-year, and 51% from 2015. There were 8 availabilities:
Upper East Side.
On Madison Avenue, between 57th Street and 72nd Street, the average asking rent fell by 9% year-over-year, to $773/sf, and was down 55% from 2015. There were 56 (fifty-six!) availabilities!
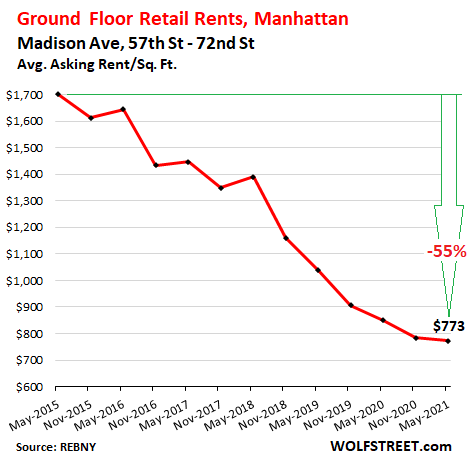
On East 86th Street, between Lexington Avenue and Second Avenue, the average asking rent dropped 9% year-over-year, despite the uptick this spring, to $311/sf, down 32% from 2015. There were 11 availabilities.
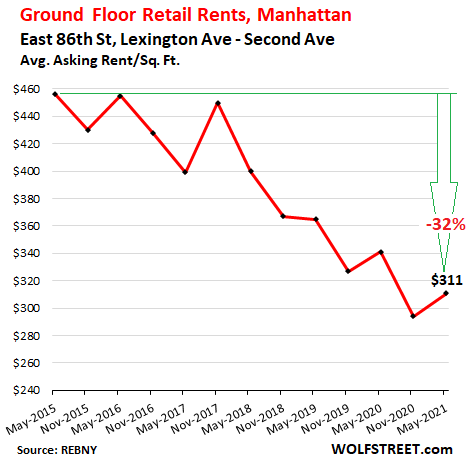
On Third Avenue, between 60th and 72nd Street, the average asking rent fell 9% year-over-year, to $197/sf, and 47% from the peak in 2016. There were 15 ground-floor availabilities:
Downtown.
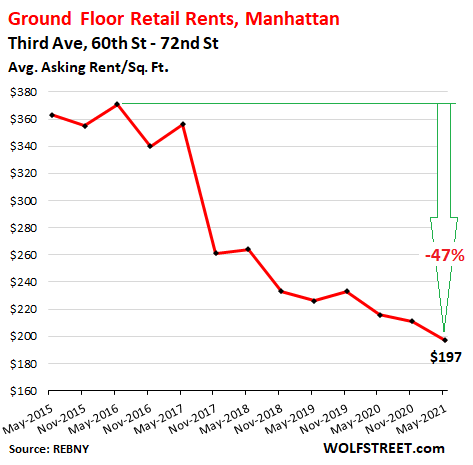
OK, this one is hopping. On Broadway, between Battery Park and Chambers, the average asking rent rose 74% from 2015 through the spring 2020. But over the past 12 months, it backed off its all-time high, and ticked down 3% to $406/sf. And there are now 27 availabilities:
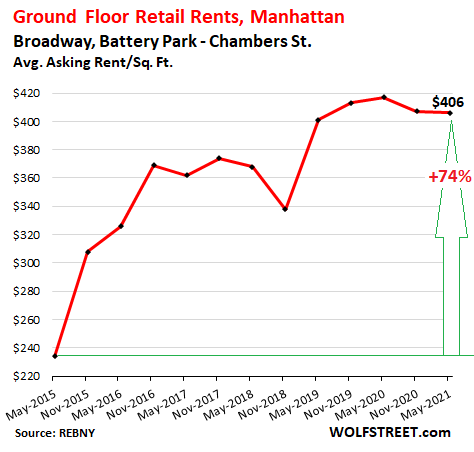
But on Broadway between Houston and Broome, the average asking rent collapsed by 37% year-over-year and by 68% from the peak in 2015, making it the biggest decliner. There were 31 availabilities:
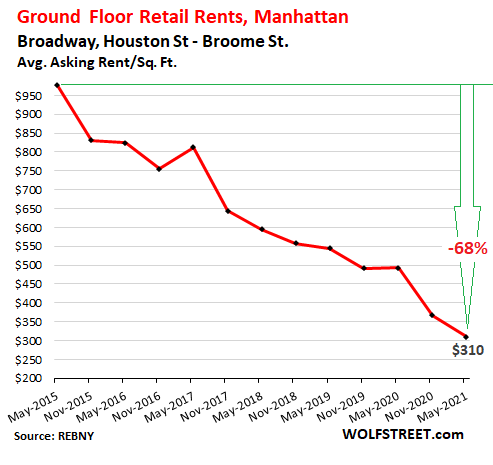
On Bleecker Street, between 7th Avenue and Hudson, the asking rent fell 12% year-over-year and 53% from the peak in 2016, amid 23 availabilities:
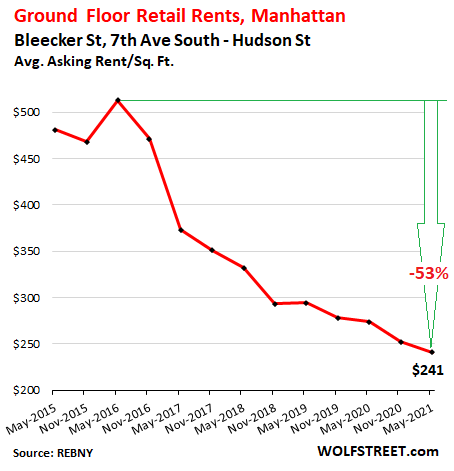
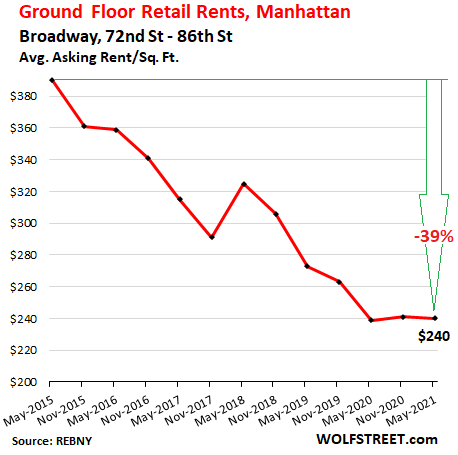
Upper West Side.
On Broadway between 72nd Street and 86th Street, the average asking rent was flat for the year and down 39% from 2015, amid 26 availabilities:
On Columbus Ave, between 66th Street and 79th Street, the average asking rent fell 6% year-over-year and was down 36% from 2015. There were 13 availabilities:
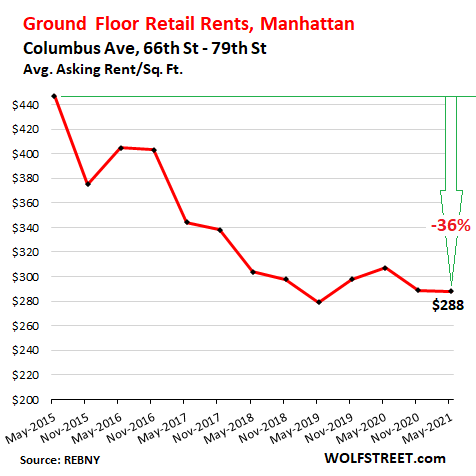
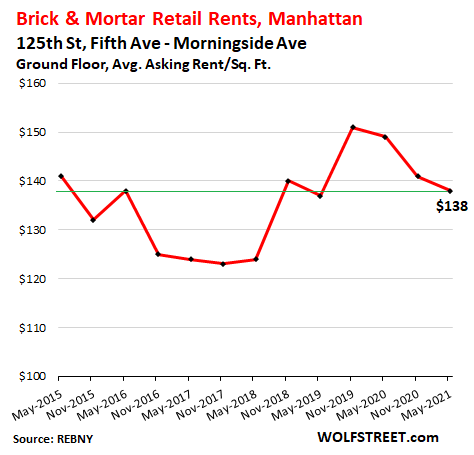
Upper Manhattan.
On 125th Street in Harlem, from 5th Ave to Morningside Ave, the average asking rent was down just a tad compared to spring 2015, after some gyrations in the middle. Year-over-year, it fell 8% to $138/sf. There were 14 availabilities.
Enjoy reading WOLF STREET and want to support it? You can donate. I appreciate it immensely. Click on the mug to find out how:
![]()


Amazon need more storage, let them convert it.
Does anyone know the future of the economy next 10 or 20 years?
I will take a whack at the next 10 years. Hangover from $13 Trillion cost of covid will be slower economic growth and more government transfer payments to keep bottom third housed and fed.
One stock market drawdown to $1500 on SP500 and a housing bust of 1/3 decline in prices. Ten year Treasury will hit 0.5%.
Just guesses.
Take a look at the weather in CA, I think that tells you something about the way the financial economy is go over the next 10 / 20 / 100 years.
As someone once pointed out, the economy is a fullly owned subsidiary of the environment.
Don’t know about that. In my way of thinking economy is mostly building on accumulated knowledge plus a system to roll the benefits out to the masses.
Russia had a lot of smart people, but not a market system to roll benefits to the masses.
Whale oil to kerosene to dual cycle natural gas to nuclear power fueling heat pump builds on human brain power making small incremental steps over time.
The USSR was rolling out benefits to the masses into the 1970s. No one came out of the 70s very well, not the USSR, not the Europeans, not the US. Those crappy Khrushchev era apartments were much nicer than anything Stalin rolled out, and if you own one today, you have a real asset.
I’m predicting one thing in 20years, a noticeably poorer populace in the US and much of the rest of the world. Living beyond your means for decades has consequences.
consequences? what are those? my next stimmie must be lost in the mail.
I read 15 – 20 years ago that the government had already promised all of the future growth of the US economy. That statement has proven to be correct and will get much worse over this decade as unfunded liabilities grow. Fed is papering it over with ZIRP.
Amen. It is ALREADY noticeably poorer but the advances of technology and the massive subsidies that the CCP has given its factories in various ways, which are selling us Chinese brand or made TVs, and more and more other products, etc., now at below their true, manufacturing cost, has just concealed the increasing poverty of the poorer 95% of Americans.
The richest Americans have been getting wealthier, because they got bribed by being allowed to get most profits and own half of each of subsidized, Chinese factories, which were so subsidized that they drove more and more US and EU producers out of business. For example, Tesla’s technology was reportedly just stolen. Will the CCP do anything to their CCP crony “perpetrators?”
Fat chance. Tesla made a huge mistake in moving to China and gifting them their technology.
It is like moving to a gang (CCP) controlled area and being surprised that the gang eventually steals your stuff. Sadly, if the CCP’s electric cars are sold in America soon at $10,000 per car, I see Americans abandoning all other cars and buying them.
That will eventually bankrupt the US auto industry. The same will apply to Boeing, etc., as technology theft or the purchase of foreign/US companies with the necessary technology by CCP cronies enables the slow transfer of more and more technologies to the CCP’s China.
Neither party is truly fixing this problem of China driving our companies into the ground. Loud noises yelled in speeches are not action. Only a boycott or truly devastating tariffs that dramatically decrease the number of Chinese or Chinese made products could fix the unfairness of the CCP subsidies.
EPM
Dunno! but you’ll be using Windows 19 to follow it.
I do not claim great expertise. However, my instincts are that the massive use of margin to purchase stock, which was covered also in this website, means that any shock that decreases stock prices suddenly will cause stockbrokers to make margin calls to “investors” that will not be able to cover their margins.
Thus, we are in a house of cards economically. One shock pushes one or some of the cards down, and the whole house of cards collapses. Otherwise, if the billionaire-owned, “Federal” Reserve had its way, it would just keep creating US dollars and funneling more US wealth to its bankster, billionaire owners and their Wall Streeter closer, like the over $2 TRILLION just gifted to them when the “Fed” purchased uncollectible mortgage-backed-securities at full price in the last year and a half.
That would inevitably lead to increasing inflation then when panic set in, hyperinflation. Even the crony of the “Fed,” Yellen, said that interest rates would have to rise in order to prevent the economy from overheating, i.e., to prevent hyperinflation, in a Freudian slip or inadvertent, honest disclosure.
CORRECTION: Instead of “Wall Street closer.” I meant to write Wall Street cronies.
It appears hybrid services of some sort, are neccessary for survival and to provide services all cities require. Does this mark the end of localy provided services, and the continued expansion of virtual yeban sprawl?
Bakeries will still be a thing in ten years because they sell very perishable goods.
Besides that? No clue.
Bars?
They’ll be no need for dating. I assume everybody will have virtual reality body suits by then. Men will be consummating relationships with 1990’s movie stars, without need to go out of the house or get a job. The house, of course, will be a 200 sq. foot. apartment unit, heavily subsidized by the top .00000001%, which will own 98% of the wealth.
The top .00000001% will be mainly comprised of owners and executives of One Corporation, the company resulting from merger of Microsoft , Apple, Amazon, Google, and several thousand start-ups. The president of the US will also “serve” as CEO of One Corporation, as well as Federal Reserve Chair and Attorney General. The streets will be boarded up. People will receive nutrition and entertainment via weekly packages sent from the government. You’ll need a permit to venture outside or congregate in groups of two or more. The only political party in existence will be called the “Freedom Party”.
Retail bakeries have been competing with in-store supermarket bakeries for years now.
In the south, there are very few retail bakeries, and even fewer good bakeries. Surprising considering the number of fat people in the south. Went to a couple of bakeries where they merely take orders from a look book, with a very small selection of pastries in the shop, ridiculous. Also, what they call French or Italian bread in the south is neither.
Not every place has a supermarket close by and I literally have seen people wait a hour to buy stuff from local bakeries. Granted that’s because corona, but sypermarkets bakeries products are usually so low quality people tend to dislike them.
And as I said they are perishable products, you can’t order from too far away or the product arrives stale to you.
Bakeries will still exist in ten years same reasons hair salons will be, people tend to prefer it.
Then again Americans have a high tolerance for bad food, so who knows?
I bake my own bread, have done since the age of 7. I use a breadmaker for normal whole wheat, and for the doughs of pizza and rolls, and most of the other breads. Tastes great, cheaper than shop-bought rubbish, always available. It takes less time to prepare the bread (2 minutes to measure the ingredients and tap out the loaf) than it takes to go buy it. I have no idea why anyone buys normal bread and rolls. Croissants I can understand, as they do take a while to do well.
It’s going to be a good show watching another round of REIT’s imploding or blocking the exit “until market conditions improve”.
Manhattan. I’ve been there a bunch…best to those who thrive on, lets just say, congestion…
Migration to opportunities is the way of history. Look out long term trend of number of Congressional seats between New York and Florida. Individuals move to where their lifestyle pencils out better.
Bricks and mortar retail is crazy. Invest your life savings to work for the landlord and the extremely high risk of going broke after sacrificing your waking life for 2-5 years? Rent-seeking is a lazy mindset, never innovating, just grabbing and that’s caught up with them now. Taxi medallions, toll roads, retail space. All slowly paying the price for decades of sloth.
As a former retailer I couldn’t agree more.
Atrocious greed among retail landlords exploiting thier captive tenant was the usual. You had to plan for it.
This is astounding. 2015 through 2019 saw steeper rent declines overall than 2020?
Where is the steep slope corresponding to the collapse in demand during the pandemic, which saw more businesses shuttered in NYC than at any time since the Great Depression? The decline in commercial rents in NYC over the last year has apparently been no steeper than before the pandemic, and in some cases, has apparently reversed, or at least leveled off.
WTF?
too soon to see those results. Just because a no mask mandate has been lifted, doesn’t make for return of retail sales., but tell that to the landlord. Landlords were , in my case in Boston, not willing to make deals. They believe that the pandemic would be a blip and return to normal, quickly. Now we are 18 months into this mess, and it looks as if Sept. of the return of workers. I will add here, talk has been shifting from hybrid to ALL return by Sept.
With that said, what pressures will exist for landlords to lower rents? It also depends on their ability to lower rents with mortgage holders approval. Not all landlords will be able to sustain themselves, it will take time for all these adjustments to manifest themselves.
Two beers,
Yes, interesting. I have been covering the Manhattan retail rent meltdown for years, and most of the steepest drops were before the Pandemic, and they were related to the toxic mix of (A) very high rents and (B) the brick-and-mortar retail meltdown due to ecommerce.
In terms of (A), rents are lower now, but still not low enough. In terms of (B), that brick-and-mortar meltdown has accelerated and isn’t going to reverse. Ecommerce has won.
Landlords are going to have to look for service-oriented businesses to fill those spaces. However, on a neighborhood basis, there is need for stores, such as the bodegas, and grocery stores, but rents must be low enough to allow them to thrive.
Any idea how long the average lease runs in NYC?
No, but I suspect 10 years for a standard commercial lease. Maybe one of our readers with knowledge of commercial leases in NYC can chime in.
In San Francisco, commercial leases usually have a term of 10 years.
During the peak office bubble a few years ago, office landlords were demanding that startups sign 20-year office leases instead of 10-year leases. So it all depends.
Do you have an estimate of what “low enough” is for service-oriented business, bodegas and other shops that can’t cross subsidize rents ,to thrive? I would assume that 3000 clearly isn’t, but is $150 – $200 low enough, or do even those rents still have to come down further for small, local businesses to thrive?
“[…]rents must be low enough to allow them to thrive.”
Even though different LLs will have different cost bases, it seems there is a general price floor they won’t test. They will compete (i.e. lower their rents) up to a point, but as they approach the floor, they slow down. If they won’t undercut each other, what kind of “competition” is there really?
For some LLs, could it be the loanable value of a property in a ZIRP/high asset inflation environment is more important than cash flow? Why be concerned about having to price your properties competitively to fill them, when you can just borrow on them and “invest” in stocks and EFT-SPAC-musk oil-dogecoin-tulips with the belief that the Fed will backstop any trade that gets TBTF?
Wouldn’t lowering the rent on your property lower the book value below what higher-asking-but-vacant rent would, and therefore lower what you could borrow against that property?
I think you are onto something here with your comments, but nothing that can’t be ultimately resolved with higher interest rates (to raise cap rates) and bankruptcy.
AF-
“[…]nothing that can’t be ultimately resolved with higher interest rates […]”
Do you expect these higher interest rates to arise somehow organically and spontaneously, in response to market conditions, or will they be implemented by central bank policy? You know, that organization that has repeatedly shown its main objective is to boost the asset values of the ruling class?
Yeah, I noticed that too. The declines started as early as 2016. Basically, the rents got so high that even the prestige retailers couldn’t afford them. When Mark Jacobs, the designer who had a whole series of stores on Bleecker Street, closed them in 2018, it was obvious the game was over. Only Duane Reade could make the rent, not a guy selling $2K sweaters. I suppose if you can afford a $2K sweater, you can afford the shipping charge if you buy it online.
The cost of real estate is being squeezed out of the retail distribution channel. Like work from home, people don’t go to the office any more, now goods don’t go to the store. There is still value in in-store shopping, but not enough to support the rents of a few years ago. The real estate market in NY is liquid, rents will find their level, valuations will adjust, tourists will come back, a new normal will emerge.
Next time you are in a store in Manhattan look down at the one foot square floor tiles. Each one of those needs to produce about ten times its cost per year in sales for sales to be in line with rent according to traditional retail metrics.
Now think about how 1400 in rent per foot implies a needed 14,000 in sales for every floor tile, even the ones in the bathroom. It’s no wonder there is no organic or grass roots retail in these locations. Very few products can generate this sales per foot.
That’s why you see only boring antiseptic corporate trophy stores in these former retail meccas.
I think retail in NYC and other expensive places will be limited to one a few things:
1) Loss leaders corporate trophy stores like you mentioned (for example, the chains can’t actually make money charging the same prices as they do everywhere else, but they will subsidize those operations with other money for the cachet of having a Manhattan store).
2) Showrooms for your online distribution operations (like a mattress store)
3) Very expensive boutique clothing and jewelry stores.
Very little else will be able to survive. Even the delis/corner bodegas need to be open basically the whole day. Look how many restaurants in the rest of the country are only open for dinner. No place in expensive locales can afford to do that.
I wouldn’t be surprised if a “Goodwill” store lands there someday. As crazy as that may sound now, it might just be the true fate of the once buzzing metropolis.
Scott,
Despite what many may think, or wish to think, the metropolis is still buzzing. It’s just that this nationwide brick-and-mortar meltdown that is also taking down suburban malls is taking down rents in these super-expensive retail locations. Ecommerce has won.
Time will tell …
1) It’s 7AM on FOX : few cars/ no people/ no food trucks, no dribbling on Sixth Ave & Rock ctr all the way to central park.
2) Side by side, where most of the coffee shops and the restaurants used to be : the whole blocks are vacant.
3) It’s a systemic change that will take decades to repair.
4) It all started after a crane banged a cigar building on W57 street, owned by a greedy landlord.
5) Many landlords expanded their portfolio in 2005, 2006, 2007, doing well, competing with each other for glory – encouraged by financial and banks matchmakers – those who expanded near market peak, couldn’t adjust rent.
6) Reality set in after 2015.
7) The frog cooking will last for decades.
8) SF & NYC under a systemic change.
Babylon and Tyre!! Abandoned cities are nothing unusual. Economics, warfare, droughts and floods. First it’s decay, then the bandits move in.
New York and other hallowed cities have no guarantees of permanence.
New York an SF always had an outsized impression of importance. Drew in the rent-seeking class, and eventually the workers fled for greener pastures.
New York and San Francisco are too crowded, no one goes there any more.
well said
Yogi Berra said it first. “Nobody goes there, it is too crowded.” I think he was referencing a restaurant.
Went to the mall. A number of stores were boarded up. Some restaurants were closed. Starbucks was closed. The ice cream place across from Starbucks was selling coffee. $2.00 regular and $3.00 large.
Some big chains and brands are gonna fall…
What I’m seeing in the fashion space is more popups. One retail label opened a popup in downtown NYC which will close at the end of the year. Saw some labels/brands sharing retail space in Miami. Each brand having its own small section and a couple of employees manning the entire space. Saw the same retail co-oping in New Orleans a couple of years ago.
Looks like long term leases are out and sharing is in. My son used to get his haircut at a popup, lasted for a couple of years in a shared space.
This is what WeWork was supposed to do, allow for more efficient office space usage. A receding tide beaches all boats.
Well, maybe not all.
You can get good deals on rent for a pop up. The problem is getting a multi-year lease at a reasonable rate.
Wewoke…. lololol…???
You can’t kill someone’s business with rapacious rent and then ask them back after you realize you made a mistake. Commercial landlords are not renting space, they are selling profits. If the tenant cannot increase profits due to low overhead, customer traffic, visibility, prestige, or other factors they will select another location. If there is no profit to be made in the available locations they will close.
Idiots. You don’t raise rent on a tenant unless you either know the current tenant can still make a reasonable profit, have another tenant you know will pay the new rent, or have an alternate use for the space that can increase your profit.
I know someone forced out of NYC due to ridiculous rent, moved to NJ, and then was forced to close over oppressive taxing and licensing. So I don’t see anyone coming back. And you know how much it costs to startup a retail business? And the regulations, federal, state, and local?
And this doesn’t even get to the increased crime problem. Landlords in any democrat run city are whistling past the graveyard. Look at Baltimore where the prime harbor area businesses are putting taxes in escrow instead of paying them until the city government gets control of the violent crime problem that is killing their businesses.
All of the new fashion labels I’ve seen in the past year are online businesses with retail being done on multiple platforms.
One minority business made a video filling orders from their live/work loft space in CA. They are using influencers to model the samples, taking orders, then manufacturing only slightly more than enough to fill orders. They are doing a couple of collections a year this way, so far. There’s no margin for retail rent in this new paradigm.
Now that I am retired fashion is a useless concept to me. I am back to clothing being only functional which means it’s all picked up at a thrift store except for briefs and socks. Shirts $1, pants $3. Fashion money better spent somewhere else, but it’s mostly a guy thing I suppose.
Then one day you are looking in the mirror at a frumpy old man in a ball cap and cargo pants. The secret is to see what other men your age are wearing, and not wear that, and that does for you what fashion does for the rest.
I hate to break it to you, but thrifting is cool.
I have only just a few hours ago, agreed with one of my tenants, that they continue to pay a reduced rent, until situation in their field improves. Gyms and such like. The cut is around 10%.
I cannot thank my lucky stars enough that they didn’t fold and vacate at the start of the pandemic. And they want to stay at least another 4 years.
What would I be doing nowadays they left? Scraping the bottom of the barrel of a totally dead commercial demand?
Landlords who insist on full rents and the additional hidden costs, do not deserve but to be tenant free and surrender the land registry papers to blackrock and other megavultures.
“Let him who is without sin cast the first stone”
How much of this decline will be blamed on Covid and the Federal Gov’t
asked to bail out these landlords? This could become a racket and a scam on the taxpayers.
Could??????
Historically these rents are still high? The end of the financial industry, or rather the transition of finance to a turnkey government function ( I think the Fed with adopt the Taylor rule), would bring bigger changes to Manhattan than WFH. Buffalo has a socialist mayor? Out with one ism, in with another.
Nobody goes to Starbucks for good coffee or food. How can food have a corporate taste? Starbucks does. Their stuff is barely edible. I used to spend money there every morning even though I made better coffee at home.
Why? It’s habitual, as are most shopping habits. It was what I did on my habitual way to take my dogs out,
I lost the habit during covid. Still take my dogs out every day, but now there’s no coffee place around so I make my own.
And so it is with lots of things now. Habits have changed.
I guess your palate is more sophisticated than mine. I think Starbucks coffee tastes great – just too expensive. Coffee should cost like 15 cents a cup, like if you made it at home.
Take out coffee is super high margin product sold to suckers who are bad at math ;) or lazy?
Well, when I was drinking it I thought it was fine, but after not drinking it for awhile and then trying it again, not so good. Maybe it was just my wallet telling me it costs too much.
In any case, people have lost a lot of their habitual activities because of lockdowns and have replaced them with other things that don’t involve spending money.
NYC leases are renewed every two years, with higher rent.
Some smaller NYC office leases are renewed every two years. The smaller they are, the higher the new rent. Same for stores.
Thanks.
QQQ targets : 348 – 355. QQQ surfed in.
My main questions is, why aren’t we seeing more bankruptcies in the commercial space? You have a 50% drop in retail rent. There must also be a drop in rents for office space. I imagine most landlords were leveraged out and weren’t factoring in rent income drops of this magnitude. I know there were a few commercial landlords that went down (like WeWork), but why not more? Were they all saved with PPP money?
I also wonder if there is a risk of cascading defaults, given banks are big commercial lenders. I guess we’ll see what happens. It’s doesn’t seem very transparent.
Well could be that there are some landlords that are not leveraged i.e. they own the buildings outright.
Today’s medal goes to any landlord who’s tenants are mining bitcoin. This Collapsible medallion has a computer chip that unlocks value. Apply it to any online DNS author who’s work you read voraciously, right off your monitor! Transfers value direct into Federal Reserve treasury. Spawns several rebuttal pieces that stroke psy-opers’ egos. Keeps the circle jerk going… Tired? Sleep in bunk bed on balcony for bonus coin.
Off topic a little, perhaps, but I just read about another collapse, this time of a whole 10-storey building in Miami?
A physical building, like, dude.
It went down like a house of cards.
I suspect that construction cost cutting in this case went right through the fibula and femur of the now dead structure.
This is bound to cool off the condo market in Miami. Really scary, probably a sinkhole.
Back in the 80’s my wife was working as a young civil engineer for a big global engineering consulting firm. She was designing some basic portions of a big development in South Florida. The crusty old senior engineer on the project told her to double the normal factor of safety for a concrete wall because he said the corrupt contractors in South Florida were infamous for mixing their concrete using seawater. That reduced the strength of the concrete and caused premature corrosion of the rebar. He said he was glad he wouldn’t be around when the buildings that were built in the 80’s got to be 40 or years old.
In the Manhattan market a 1000 sq ft can be 850 or less of actual sq footage. In the past the land lord will insist on the inflated footage. Take it or leave it. If the drop in rents has corrected this land lord BS of inflated sq footage then a 50% drop has accomplished something. If not then another 50% drop may .
Dr : your 850 sq ft office/store benefit from a men’s & a ladies room, the elevators area, the front desk, the basement, the super office…
They don’t come for free : 850 net, 1000 is gross.
It would be nice to know the rents back in 2000 to get a better feel of how out of whack the rental market in Manhattan became.
1) Those chats might explain why the 10Y is < 1.5%.
2) There are 13 charts on this blog. Only Battery park is trending up. Harlem in TR. The rest : lower lows, lower highs.
3) NYC is much more important than SF and Portland, or San Diego, with all the respect.
4) The banks, which are NYC largest landlords, absorbed their losses.
5) In other cases, banks took over landlord collateral, their other buildings,
6) Banks absorbed zombie assets since 2008.
7) E commerce did not cause the death of Manhattan. Greed did it.
8) Those 13 charts shows that the US economy is.
9) The pandemic accelerated the downtrend and there is no vaccine for Manhattan.
10) QQQ all time high. $NYFANG lower high.
consequences? what are those? my next stimmie must be lost in the mail.
dear Wolf, forgive me in advance this diatribe. please amortize across all the posts i didn’t post in! i need special comment plan.
and forgive again while / if you’re in the forgiving mood: i must admit i didn’t yet read the article; i came here for Petunia because after breaking up with Corky and Basul, it lit a fuse on blowing up my entire life along with another set of illusions.
but it was you- it was WOLF, himself, who forced me to come back and write even as i’m trying to spend my internet time on ecosophia now so’s i can figure out THE ILLUSION and try to come up with an alternative to the hell that’s been created when the world is miraculous, AND as an artist who feels wholly irrelevant among nothing but other irrelevant artists and thinkers…
Wolf said ecommerce WON.
and that’s what’s horrifying me: that after these shut downs, everyone’s not only content to concede defeat on our own romance, family lives and whatever else that was good about being alive, we’re not even CONSIDERING fighting back or coming up with an alternative–ANY alternative–to the …to THIS. ALL THIS.
so Petunia says all this great stuff and i’m about to type in my excitement under hers about all the pop ups… but even fashion isn’t saying anything anymore. they are irrelevant and hopping around trying to make a living doing anything.
as a former writer, i’m now constantly asking: WHAT’s THE STORY NOW?
it’s not about “getting the girl” anymore because she’s not a girl and if she is she might be a lesbian who hates you or an internet girl who sleeps with everyone online she swiped left and right on and has a baker’s dozen abortions and will ruin your career because you touched her shoulder and made her feel uncomfortable unsafe and then you find your girl and have a baby but by then your countrymen and women tell you to get over your assumptions that you should have a LIFE at all. you’re entitled and god help you if you’re WHITE and a man!
now you’re out of fashion like natural eyelashes and eyebrows that aren’t alarming from across the parking lot.
sorry for the rant. i’ve been sobbing in public even but i know it’s necessary. i’m lost stuck and don’t want “pop up” anything.
i want people to at least wanna fight back by not just passively letting “ecommerce win” because we’ve lost good music and sexiness already and i can’t even joke in san francisco without ending up in an alternate reality of wrong words.
i read a NYTimes article about some famous fashion designer who was pumped and dumped as per the model because even longevity in a BRAND is irrelevant. cynicism is the go-to model.
come ON. there has to be the loophole of loopholes in this entire system and philosophy of ..whatever this is now.
i can’t get rid of the internet. the thing that ruined life and the magic phone that did unspeakable things to the corpse under the proverbial mattress.
i’m asking the wrong questions. until i think of the right questions, please… Petunia you ignored my leggings question because you thought i was crackin’ on you and i’m NOT. it’s about something ELSE. what’s next?
that’s why we’re all here, but it’s all feeling so binary, so … contrived. like our options are given to us as acceptable choices.
when designers are popping up and around trying to make a living while others are trying to hop on their corpse for their boots, rings and tin foil fillings, you can’t even hope to outrun such a type of THINKING.
it’s so tired. trifling. that’s the word. it needs an old fashioned shaming word.
what are we supposed to do to win back our own reality culture and dating in real life? the internet is making women here insane. i tried to introduce a woman i know to James and she saw his photo and thought he was so gorgeous she spent the week losing her phone, crashing her car, and showing up late to work.
then she bailed.
i just saw her and she said she was so tired because she’d spent the night with a “boy” (from the internet). / she was bragging and i shuddered and wished i had a mask on to cover the curling of my lip because this is Progress. this is Feminism’s wish coming true. as long as we don’t slut shame it’s all okay.
another way, people! we need one! another STORY.
where’s Unamused when you need him? he’d have answered the leggings question were he still here. he’s so used to occasionally lurking i fear he got bored and actually left for good. found something better in the Real.
like a way around the insanity of the financialization of everything with the insanitization of the world and our inability to … fight against ecommerce winning.
as an artist i am lost. i’m supposed to make this humanity and grinding and kissing and dancing and laughing and loving and hugging “thing” look good. at least better than the crap we have now.
sorry, Wolf. i did okay with the sex stuff. got perilously close to saying if they’ve got us by the short hairs, can’t we get little Vietnamese pocket ladies to wax it off?
something creative… i’m just throwing chum out there. even chum is sexier than internet porn in this cynical world now. post chum is sexier than internet porn.
so back to The Story… we have a world of empty buildings and because of rent and regulations we’re living in vans and …???
what’s the vision the story now that it’s NOT about getting the girl because she’ll take your job and your kids and the house and leave you on the meridian washing your windshield.
women–Feminists–here will be angry at me for not asking what women’s vision is: WE’RE LIVING IT AND WE GOT SOMETHING HORRIBLY WRONG. i don’t care who really won the election back to the hanging chads— i want a total “who’s ideas was THIS?” do-over.
i’m asking because now that i have blown up everything, i’ve got room for new ideas and i’ve had my ass and emotions publicly splayed everywhere i’ve been like a trail of despondent slime, so i’m game for anything. except for sexting and internet courtship.
Real Life. please. let me come back at the end of this weekend (much sewing and focus to do), please let me come back and get an answer from Unamused in drag since Petunia has forsaken me.
(she’s holding back. / she hasn’t had it bad enough yet to be against the wall at the end of the alley and follow through her co-op biz idea. she’s from MANHATTAN… they’re born thinking of eco-systems to support their ventures so’s they don’t have to whore themselves out shamelessly. for a former time Manhattanite to promote themselves, they were half lidded and maybe said “jejune”–in regards to YOU).
Petunia doesn’t want to CARE too much. / i’m doing one of my mind fucks where i try to incite one’s interest from afar but she’s good. much better than me. she thinks she’s nearing retirement age.
i’ll sell rubber ducks to get her out here so’s i can get her to CARE. then she’ll have a plan. watch. other women here watch Petunia, too. when SHE goes ot the ladies’ room, we suddenly have to go, too.
where’s the loophole? or the new story? ecommerce cannot have won. it already has your genitals locked up in a display case and you have to ring a mockingly red buzzer to call staff to come unlock it for you.
i’d say it’s long past time for The Loophole if we cannot yet come up with that New Story. i’ve lost the plot anyhow.
i’ll be back sunday night. please Wolf don’t delete. please others answer with ideas. no complaints. that’s like coming in my face at this point. screw commiseration. / it’s passive.
x
The future is going to happen with you or without you. Your choice.
Dear Mr Escierto-
your NAME is more beautiful and melodic than your platitude cliche of a trying to be tough answer that says nada!
but thank you; i figure you were just trying to say hi like how dads do. with advice.
(smile)
thank you Mr Escierto.
x
Read some history to get some perspective on what happened after people went through this type of mass insanity before – Romans, French, Germans, Chinese, Cambodians. When you think you got a handle on what may happen, think of a plan and take the actions to implement it – survivalist, move, new business startup……. It helps to identify like-minded real people to work with. Positive forward action toward a goal is far better than twisting in the wind.
Good Luck.
thanks, Mr Joe2.
twisting in wind.. yes. i’ve been doing that.
history… yes… history is the future…
thank you for the hints.
x
Kitten Lopez,
“…as a former writer,…”
Hahahaha, that was funny. Or sad. You’re a better, more powerful, and more current writer than ever.
aw, my dearest Wolf! you’re all heart. i’m going to copy what you wrote and keep it on my open doc i never close so i can REMEMBER certain things.
as for you being my friend all this time during one of the most difficult times of my life, thank you for putting up with me in person in work and on here. you’ve kept me contained when i needed it, fluffed me up like a pillow full of dandelion seed when i needed it, as well as given me room to practice here and at home or on my own abandoned site. you gave me home here and kept me strong moving and “lubricated” so my screams aren’t rusty scratchy and warbled and i may find answers in my own words.
you mean more to me than you know or maybe you know. sometimes it’s easier for me to write my gratitude than SAY it. and you’ve kept me in this game and not feeling like i’m in outer space so much.
thanks, dear Brother dear Friend. you are kin now i am always at your service. i’m crying now because your words are so kind. i feel a mess to be honest with you. / but i’m okay in it, it’s not a forever thing. just a phase.
(smile)
xxxxxx
most important, in a world of constant lies hypocrisy and shtick, thanks for constantly/continually being the man i thought you were.
when you stand up like you do, my entire being curls with glee like my toes of joy because you keep romance and all my most epic beliefs alive regarding honor and strength.
thanks for all you do and i am forever at your service. / we’re good; we’ve already fought through stuff. after that it’s easy.
(huuuge smile)
x
Good read to the last drop
Thanks for the heart based write up of where you are today. Remember that tomorrow is a brand new set of downs.
Remember you have the chance to breath. Even if only for today. This is a gift that most can’t grasp. Take a deep breath and think of what YOU are playing for. 3, 5, 10 year plans
Dear Mr Nathan–
that was SO funny: “remember that tomorrow is a brand new set of downs.” i laughed just re-typing it.
and thanks for the reminder to shake it off and plan in increments. INCREMENTS!
i’ve been on the 20-year-OH-MY-GOD thought train going in circles.
James is ahead of me and has already broken through to the “well, the mid-70s were bleak. remember the music? the cars? our parents’ narcissism?”
thank you for taking the time to write.
x
Minor thought here, what if these locations were turned into legalized brothels and weed shops (think weed version of Starbucks). That could bouy rentals couldn’t it?
No amount of e-commerce could replace the #1 profession in the world….
Actually, never mind, with the way the value of the dollar is changing, it’s not at all obvious at all either of the aforementioned will survive, especially with the availability of online porn and improvements in AR/VR.
I’ve indeed noticed that my neighbors never go shopping anymore. They get everything delivered. The lobby is like Christmas eve on most nights with packages for every floor.
They barely even walk anymore. They Uber while cheering climate change stuff.
They’re getting fat too.
They don’t take the subway anymore coz too many minorities might contaminate them.
It’s not the old Manhattan. The class supremacists are destroying it.
While their self righteousness gets more and more toxic everyday.
that was a good post, Miss Marie. connected to one below.
x
Cities reinvent themselves. NYC was being killed by high rents that suffocated business innovation. All the interesting retail was squeezed out by 2016. Neighborhoods like the East Village were disaster areas full of junkies, criminals and the hopeless. SoHo was a hollow shell left when manufacturing pulled out. Both of them were reinvented. They became bohemian, then trendy, then chic and then expensive and stagnant. There’s nothing like economic collapse to create space for revitalizing a neighborhood. In fact, it’s high time the rents came down. If every damned lot is no longer an asset subject to savings glut fed asset inflation, maybe new businesses can form.
that cities re-invent themselves is an old trope that is slightly different with the advent of the magic phone and internet killing anything new secret or different. the ecosystem of creativity is GONE, and as the artist scrapper/producer at the bottom, my despair has been mostly because as Miss Marie said above you:
“…my neighbors never go shopping anymore. They get everything delivered…. They barely even walk anymore. They Uber while cheering climate change stuff…. They’re getting fat too. They don’t take the subway anymore coz too many minorities might contaminate them.”
young people are terrified of life and each other and everyone else and it’s made people mentally ill. there is no ECO-SYSTEM so you’re always pitching something shallow and passing.
as an artist and repentant writer, i’m trying to find the new STORY.
after talking to James and reading these comments and those on John Michael Greer’s ecosophia (i fancy he’s Unamused’s alter ego), i’ve decided yeah… screw trying to convince anyone i’m having too much fun over here.
i’m just gonna HAVE it. i can’t build an eco system on my own.
or can i?…
x
THE AUDACITY OF YEAST…
i once told Unamused that i was going to think long and hard about something to say (write) to him via the comments section here; i invited him to return at a later date, as i did with everyone here or anyone who answered me.
that was a test. for him and for me.
because if he shows, he drops beneath the surface of fast-paced news and comments and gets a good piece of me that usually takes intimacy in real life to get.
and if i show, i believe in magic romance and secret 5D moments that make the 3D all worth it.
the magic phones took that away.
the internet killed the nineties dead and all that came before and after… need i say more?
we’re now left without our own local eco-systems. ecommerce has won and so has untethered absurdity.
i see this story is so far down the list because of it, and i feel safe to announce that yes:
LIKE SOURDOUGH YEAST, I WILL DO MY OWN THING IN A BAG OF FLOUR ISOLATED IN A CLOSET AND WILL COME OUT AND MAKE BREAD RISE EVERYWHERE FOREVER.
or until the next cycle of despair repeats itself. i am only one megalomaniacal Leo with it 5X in my chart. just noticed that as i’m looking into this stuff and figured that’s GOT to count for SOMETHING that i can later use to explain the hail mary pass that i’m planning as the rest of my life, as my gift to Humanity.
(even i’m laughing. barely. through my TEARS.)
ecosystem:
without proximity to each other, along with affordable rent, there are no artists musicians poets thinkers or funky entrepreneurs club owners able or willing to take a chance on making all our lives more interesting.
you will be relegated to finding your partners by swiping screens and hoping the older successful ones have a harvest of eggs frozen somewhere.
ew.
the world is run by STEM people, Feminists, the Fed, along with other of the illuminati, and this is why you don’t know about the beautiful prolonged agony of grinding your beloved after weeks of just holding hands.
as long as puffy, incapacitated work-from-home people are taking up all the best city apartments and rent can’t go lower and we have to work 67 gig jobs to service you in your cul de sacs, we ain’t none of us going ANYWHERE.
that’s why everything will stay online until it all breaks for good.
or until you all get good and BORED enough or see an alternative to meeting new internet dates on all fours.
there are no loopholes apparently.
but i’m the loophole.
if anyone has come back here for The Secret Kitten, i have put in writing that i will no longer look to the world to join me. i’m going to pull back the curtain on my own fun ME ME ME world over here with James and with Wolf, my last remaining friend in San Francisco–no, AMERICA.
it’s on.
but watch.
look what yeast can do. and no, i’m not inspired by yeast infections; i’m inspired by San Francisco sourdough.
that and Lawrence Chew was on the air (KPOO), talking about how this one star of his neighborhood, a guy just a year older than him, class of ’72 at Wilson High, inspired all these younger cats to be AMAZING athletes and men and boyfriends and husbands to their women. he had the best parties and people stayed to talk to him for HOURS afterwards.
yeah, like THAT!
he said it was ONE GUY because when he’d broken his arm in the first half of a football game against Lowell High they’d been winning up to that point.
the Audacity of one little Yeast that Could. that’s what i’m gonna go title this as my dare in writing here on Wolfstreet.com in this year of our Lord (whatever it says on my post).
it’s on. let the yeast RISE!
thanks again for those who commented above. and have in the past. this place is like my bag of flour in the closet, but with the publicity of a Times Square screen tickertaping out my next quest.
how to scare yourself into going all out. like wearing LEGGINGS when your ass is at its worst so you’ll make it better because the PAST isn’t as embarrassing as now. no matter how long facebook lasts.
talk about yeast!
x
p.s. speaking of which–where’s Lisa Hooker?
(wink)
p.p.s. i don’t know if Unamused ever passed that test and came back to read what i’d written. / i’m only supposed to know the results of MY tests for me.
x