Sales of “existing homes” performed the same trick. The phenomenon is getting established.
By Wolf Richter for WOLF STREET.
OK, this is now following the same script: Despite supply that has been rising for months, sales of new single-family houses by homebuilders to the public in May fell 6% from the prior month to a seasonally adjusted annual rate of 769,000 houses, down 23% from the recent high in January, according to the Census Bureau this morning. This sharp decline in sales occurred amid spiking prices.
A similar phenomenon has been playing out in “existing” house and condo sales, where inventories rose for the third month in a row, and yet sales dropped for the forth month in a row amid a historic price spike. Something is out of whack.
The sharp drop in sales of new houses over the recent months brought them back to about pre-pandemic levels. And following the construction boom in apartments and condos over the past decade, single-family house sales are far below the boom-and-bust years of 2002 through 2007:
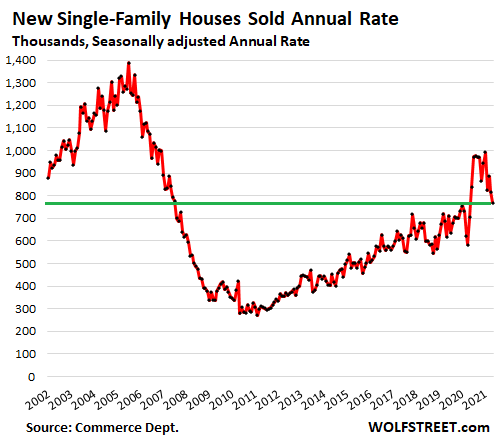
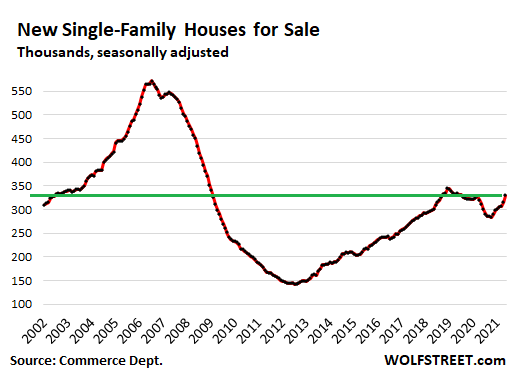
Rising inventories. Homebuilders are busy. They’re building. They’re adjusting to the new market where the sudden burst of working-from-home – potentially a long-term shift for many home buyers – is now being built into the house. And there are plenty of spec homes available for sale.
The number of unsold speculative houses rose for the fifth month in a row to 330,000 houses, seasonally adjusted, at the high end of the spectrum since the housing bust. And supply at the current rate of sales rose to 5.1 months.
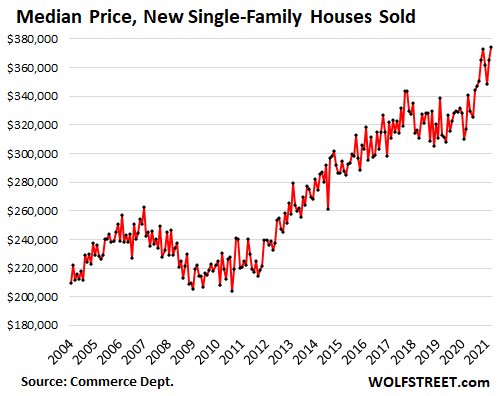
So despite all this, prices spiked – what else is new? We saw this yesterday with sales of existing homes, where prices spiked 24% year-over-year in May, the largest price spike on record, despite rising inventories and sharply lower sales. And we’re seeing the same phenomenon today in new house sales.
The median price of new single-family houses rose 2.5% from the prior month, and spiked 18.1% year-over-year, to a record $374,400, eking past the prior record of January:
These new houses are sold by homebuilders to the public, unlike “existing” homes, which members of the public trade among each other. This changes the pricing dynamics. When money from the Fed and the government gushes through the streets knee-deep, and when people are looking for larger homes to accommodate one or two offices, then homebuilders attempt to accommodate them, including with higher price tags.
Houses that sold for over $500,000 accounted for 24% of total sales in May and April, the largest share in the data. And houses that sold for over $400,000 accounted for 45% of total sales, also the highest share in the data. The dollars are flowing freely. People who buy houses are stepping up to the plate.
But the number of people willing or able to buy under those conditions is shrinking. Some might be taking a step back to watch this housing bubble from a safe distance. Those are the people that went on buyers’ strike. Then there is also the shift to working from home that may have run its course, with companies switching from remote work to a hybrid model; after the initial flood of work-from-homers was accommodated, the red-hot demand for new single-family houses might now be in the early stages of cooling off.
Whatever causes this sharp decline in sales from the red-hot levels a few months ago both with new houses and “existing” houses and condos, amid rising inventories, indicates that there are potential buyers that have gone on strike under the current market conditions.
Enjoy reading WOLF STREET and want to support it? You can donate. I appreciate it immensely. Click on the mug to find out how:
![]()


For the love of god, really hopelessly hoping this is the on going trend and will pick up strength to burst this bubble hard. Pipe dream but that would be the only chance regular middle class folks can afford a decent place that’s not completely out of whack from income. Looks like MSM is already out in full force in damage control again with these downward sloping numbers..saw this on the Altantic today. Yup, your usual narrative of, can’t envision a bubble here…supply is low, demand is still high and this downward trend just people taking a break.
In the meantime, wonder if this will reverse course at least in California soon since Newsom decided to pay back rents to cover landlords…should inject some more steam into the frothiness and remove that urgent need for these mom and pops to offload soon.
“he 2021 housing craze feels as sudden and shocking as the pandemic, but it was decades in the making. The emergence of the huge Millennial generation in the 1980s made strong housing demand in the early 2020s entirely predictable. The Great Recession’s clobbering of the construction industry made today’s housing shortage equally foreseeable. Indeed, McBride, the economics writer, saw all this coming from a mile away. So, I asked him, what does he see happening next—a rise, a crash, or a plateau?
“It’s not clear at all to me that things are going to slow down significantly in the near future,” he said. “In 2005, I had a strong sense that the hot market would turn and that, when it turned, things would get very ugly. Today, I don’t have that sense at all, because all of the fundamentals are there. Demand will be high for a while, because Millennials need houses. Prices will keep rising for a while, because inventory is so low.”
The only places where McBride told me he could envision a bubble bursting are locations where urban residents bought second homes in a panic—only to have the urban core quickly get vaccinated and normalize in 2021. “We might see some price declines in the second-home areas, like small towns in New England and other beach towns on the East Coast. But even there, we just might see a shift where more people decide that they like owning second homes.”
Lots of erroneous information here about population, etc. C Hamilton at Economica has detailed blog on demographics with recent article about declining population of under 60 group and charts for west, south, east and midwest and its affect, effect on housing. Very detailed and when meshed with a number of his other charts, graphs, info on population gives a much clearer picture and what is happening and coming.
The Bubbles are playing in Candlestick Park this summer, after Gretchen and Biden empty the pipeline. I’m hoping to be there. Bang on the van, chase ’em down the street… Love the Bubbles, waited long enuf!
It is amazing that there was even a Housing Bubble 1.0 considering the ugly demographic trends that were in the immediate offing.
But…behold the idiot power of ZIRP.
Thanks! I went to check out the blog
If the dollar would have kept it’s value, the housing market would indeed be a bubble.
However, they injected an insane amount of helicopter money , shut down or hampered production and services and on top of that reduced the number of people willing to work with an unemployment check higher than the regular pay.
No need for a triple phD in economics as Wolf may have is needed to understand that this will result in super inflation.
May be if they vacuum up money with higher taxes but that would come from those with high AGI’s who are now scrambling to safeguard their savings with for example a 2nd home or a new home in a low tax state and keeping their old home.
And those who move have no reason to sell immediately since they just secured a nice fat mortgage at 3%, way below inflation and their old home, likely that has appreciated more than 500k so if it goes down because the bubble burst’, no sweat since it would only be against less capital gains of which more tgan half is slready taxed away (since april 39% + 4% + sucker state >10-15% + local tax whatever)
So more likely houses will stabilize or go up in nominal value just because inflation is now double digits.
And that will fuel more demand because more will scramble yo protect their savings.
But may be i am wrong and the new magic is you can print money, reduce supply, give helicopter money and prices will not rise but drop.
Who am I to say?
How come when rich people’s wealth climbs through the roof no one around here bats an eyelash? When Bezos goes from being worth 10 billion to 100 billion in 10 years, no one flinches. But if you raise regular people’s salaries from $11 an hour to $15 an hour screams of “Weimar!” and “Armageddon!” rise to the rafters? The top 1% have seen their wealth rise over $11 trillion dollars over the past 20 years, but all that purchasing power is just dandy. But even the thought of Joe and Jane Blow seeing their wages rise at a much slower rate brings on the vapors.
Well one answer to your question is that companies don’t raise their prices when Jeff Bezos’ net worth goes from $10 billion to $100 billion. But they do raise their prices for everyone who buys their goods and services when their workers’ wages rise. Latest example is Chipotle raising their prices 4% to pay for their workers’ increased wages. Add up all those single or low double-digit price increases across the economy and it becomes a very big deal for the bottom 50% of the population.
Actually, per Matt Stoller, an antitrust suit has recently been filed against Amazon that alleges that they have effectively raised prices across entire industries in a way that certainly has enriched Jeff Bezos. The suit argues that Amazon raised prices to cover the cost of “free” shipping and enforced clauses where Amazon sellers can’t list items more cheaply anywhere else so that prices for certain goods in the entire market increased. Amazon’s reach is just so large that such price increases are far less visible.
Mice are too afraid to tie the bell around the fat cats’ neck. Instead, they will joyfully rip into their own.
Bezos going from 10$B to 100$B does not result in him having 10x cars, houses or 10x tooth brushes. His money stays invested and thst 100B$ is funny money anyway. If he would sell, 40% goes to Uncle Sam and his stock would tank
If however you helicopter 90B$ around , that money is going to be used and consumed, driving up prices
Assuming people on unemployment are just rolling in the dough instead of “just getting off their lazy behinds”, how exactly are they in a condition to be buying houses? People who are making that amount of money couldn’t even have bought houses at the absolute low of the Great Recession, let alone the stratospheric heights the housing market is currently at.
People “sitting on their lazy behind”, your words, not mine, those people are smart.
They figured out that they will not earn more if they start working instead of the covid cheque.
The problem is they produce nothing or give no services so production/services is lower while the same or more money is available for less goods and services to buy.
Step 1 – within the next few months, the Treasury runs out of money in reserves and must float excess Treasuries on the market every month. After a few decent auctions, the buyers strike.
Step 2 – Interest rates of all kinds start to zoom higher.
Step 3 – With higher mortgage rates, the balance between buyers and sellers is reset. Lots of pandemic programs begin to expire and we are left with high unemployment rate and still fairly high inflation. Prices always follow supply and demand. Home and asset prices begin to drop. As asset prices fall and with higher interest rates leading to higher monthly payments, the onslaught of people trying to sell houses stacks up.
Step 4 – Banks start to feel the pain as buyers walk away from mortgages.
Step 5 – Biden’s BS agenda is thrown in the trash. The stock market plunges and instead of living in a bubble, many people are living on the streets. Massive unrest.
Step 6 – China uses US weakness as an opportunity to establish dominance over the whole Asian sphere – essentially locking down all shipping around South Korea, Japan, Singapore, etc. The lack of investment in manufacturing in the US brings the economy to a screeching halt.
Step 7 – US leadership is destroyed as Washington DC goes on a political witchhunt of epic proportions that accuses anyone who is not woke and liberal of being an enemy of the state. The new fascist liberalism has accomplished its goal of destroying the world.
Wake up america. Woke is broke.
@gametv.. You forgot the first two steps We blue 10 Trillion on our third endless loosing war. And two Republican Presidents enacted 2 deficit busting wealth transferring tax cuts.
@gametv.. You forgot the first two steps We blew 10 Trillion on our third endless loosing war. And two Republican Presidents enacted 2 deficit busting wealth transferring tax cuts.
Transitory. Just drop more $ onto the market and the curve will change.
Either that or Blackrock will start buying up whole cities…. (I did read the article and know they are buying up a company)
?
That’s another huge problem that will unfold later… from what I gather Rent To Own lease purchase options have the highest default rate of any form of home ownership other than Habitat for Humanity
Real estate investment is a great business model with generous tax write offs if you don’t sell owned rental property for 30 years
Ron – Real estate has been a great investment. It benefitted from more 2 income families and then from lower interest rates. Both those trends are broken and now real estate is an inflated bubble.
TRUE Ron,,, but only IF you have an enforcer:
One way or ‘nother, an enforcer is required in many areas, of course we cannot know about all, eh,, and although not ever qualified myself, I have known a few:
Without exception, they were true to their word, and their word was, ”pay up and clean up or be gone with no chance of security fee”
Seriously going to be different this time, as always, while similarly seriously ”being the same”,,, also as always…
Oligarchy and others close, think they can protect themselves with fences and mercenary, but his and her story (s) suggest otherwise, though not clearly ”proven” by any means, yet,,, eh?
Maybe the potential buyers of new homes are not on strike, maybe they just hit the wall of affordability and the new homes on offer require income streams and down payments that are higher than what they can afford.
Amen. That is where the tire meets the road and the laws of physics take over despite our wishes. However, keep in mind also that more and more people are realizing that we are in a 1929 style bubble but of everything, including real estate. See “Margin Debt and the Market: Up 1.7% in May, Continues Record Trend” in advisor perspectives. Thus, buying real estate that will see a significant, impending reduction of value this year or next year is not wise.
I would never short the market, because the true ultra-rich families, whose advisors control the markets via their control of those fortunes like Megalodons would dominate a lake, can still probably manipulate it significantly and delay the inevitable. Nevertheless, as with the rules of physics, we are getting to the point in which basic math, the size of the US government’s rising interest payments, the poor prospects for growth in an economy when one of two parties is rooting for its collapse and the ultra-rich are still keeping most investment and jobs in China due to US foreign income tax loopholes, one party refuses to require the ultra-rich to pay even a fraction of what the rest of us pay, the demographic percentages of its population point toward increased entitlement payments, while immigration is feared due to racism, etc., will drag these bubbles down.
A reputed agent for the ultra-rich, whom others believe was very rich, tried to forestall a financial collapse before. It did not work. Ultimately, it will not work now. I am selling a lot of the stock that I own, and expecting the rest to collapse significantly in value.
China is buying the manipulated-price gold from the world, as is India and other countries to lesser extents. I wonder if Fort Knox has any real gold left.
However, given recent events, I would not bet against the rest of the world becoming more and more enraged and retaliating by boycotting the products of Chinese factories given what is coming out. Thus, China may need to sell large portions of its gold reserves if that happens.
To clarify my own cryptic comment, if a group of countries decided that the CCP was to blame for the last year’s financial catastrophe, which I opine is probable, the resulting boycotts or ultra-high tariffs may force the CCP to sell its massive, gold reserves to acquire necessary materials if its income from its exports were to drop precipitously. That would collapse the currently manipulated price of gold, which I opine should be higher if it was not being manipulated.
Remember that a lot of our stock index funds are foolishly investing in CCP-controlled Ponzi schemes, which are called mainland Chinese companies. If the CCP were to be pushed to sell those massive, gold reserves, those Ponzi schemes, with their Enron style financing might not get bailed out. Thus, huge losses will then be incurred by the foolish US and EU investors in the CCP-controlled companies, whose finances are carefully hidden by the CCP’s orders, to conceal their Enron-style finances.
Such a systemic shock from the collapse of the CCP Ponzi schemes-companies now listed in US stock exchanges and the resulting collapse in the value of US stock index funds will drop the WHOLE stock market like a rock, just due to the panics and shock that they will cause. Index funds probably have long-standing plans to sell rapidly if their index starts to go down significantly.
That is how stock market collapses happen. If stocks start going down, the huge use of margin by all US investors will force stock brokers to make margin calls and when foolish, over-leveraged investors who bought stock that they could barely afford cannot meet the margin calls, the stock brokers will be forced to mitigate their damages by selling the stock that was bought on margin.
That is a lot of stock that will suddenly be dumped on the market. It will be 1929 all over again. The protections in the stock market will not be enough to stop the collapse, because stocks are so RIDICULOUSLY overvalued (given their limited income growth prospects and price earnings rations) and the use of margin is so ginormous.
The alternative may actually be worse. If the billionaires’ “Fed” can keep the party going with the collusion of other central banksters and its EU and US billionaires printing money to buy the collapsing stocks, we may get Zimbabwe hyperinflation and little growth: stagflation.
In my average midsized Midwest city, the trend building up over the last few months is that prices are still rising and inventory has vanished. Some real estate agents have actually taken second jobs and a small number have actually quit. Some jobs in the area, that require only a high school diploma are paying nearly $20 an hour (17 to 18 at exact moment, but still trending upwards). For now at least. I don’t expect the high starting wages to stay that high for long, once enhanced unemployment ends, and so some real estate agents who have quit, might try to get job back later.
In my area, for now at least, homeowners aren’t selling, this could be because of demographics at the moment, possibly that upgrading is too expensive, hidey in the house mode, enjoying the summer, and many other factors.
For reference, in my area right now; a very typical, suburbia like 2,500sqft 10 year old ish house in a cul-de-sac in a subdivision, near likewise houses, is currently roughly $260,000.
The house prices, though rising, are largely set at the moment for average and cheap houses, in that this house goes for that amount and will sell for roughly that amount. House sales for average and cheap houses are going very fast. Recently, there was one house listed online by a local real estate company and it sold in under an hour. Someone found it online and had already called up the agent and agreed on a price with the seller to write up, less than an hour after the posting went live. It’s worth noting, that typically real estate companies take a smaller cut of house sale, if house sells super quickly, typically, this is something like pre the open house.
Nicer houses are going up in price very fast and take several weeks to several months to sell.
For the rest of the country, I expect that many, would be homebuyers expect, that next year building supplies and many other things will partially drop in price to prices closer to pre pandemic. They would expect house prices to drop and that it would be unwise to buy now. Inability to buy at current levels is of course a reason as well.
Taxes have stopped me from upgrading ridiculous in Nebraska why we have 3% unemployment can’t afford taxes school s and bonds but dumb people keep passing bonds if you give government money they will waste it
In my neighborhood of LA the starting price for house is 1.6 million and that gets you squat. Very few listings and the ones that are listed are flips of homes bought last year that are now priced 30% higher, although they are fixed up inside.
Hey, the pandemic protocols were just lifted, so everyone is just not making changes. As things open back up and some normalization occurs, the buyers of this year will be trapped in a market with falling prices and rising interest rates.
This is just supply and demand.
To specify, there are still houses available, there are just alot less than normal.
Rising supply AND rising prices: a trend that can continue forever, right?
Compiled with a generation who isn’t having kids at nearly the rate seen by any previous generation and thus doesn’t need a 3-4 bedroom home.
As the VP of my team would say “somethings wonky here”.
Also, the rate of single people is greatly rising.
As the booomers retire and pass away, there will be a large increase in supply of used houses.
In the California desert, I’m seeing perhaps one new listing per week in a retirement community of several thousand SFH. Even with an asking price of $50,000-$100,000 more than last year, they sell in a few days. Before I relocate somewhere else, I’d like to see data on the state of bidding wars throughout the country.
Am I the only person who thinks the Fed should be abolished?
No, Confused, which rhymes with Confucius, get Ron Paul’s book, “End the Fed”, first published in 2009, and see that there are many cogent arguments in it to send this bunch of double-talking financial amateurs to Siberia for retirement. The movement will experience a groundswell when the current bubble burst the day after tomorrow.
It should absolutely be done away with.
No doubt this report was compiled before yesterday’s pontification by J “Inflation is temporary” Powell
I read comments on this site, and I realize there is a lack of inflation knowledge.
You see, there are two types of inflation. Demand side inflation and cost push inflation.
Usually, we see demand side inflation. Less frequently, we see cost push inflation. This time, we are seeing both at the same time.
Reading comments, it appears everyone is only familiar with demand side inflation. That is error in the analysis ….
You see, cost push inflation can keep prices high or even rising when demand slips. That is what the new housing market exhibited today.
But, getting both demand side and cost push inflation at the same time is an unprecendented event. A new inflation chapter will be written when this is over.
Inflation expectations are well anchored can’t you tell by listening to JPow talk it into existence like some sort of econ hypnotist?
People are very well aware of “cost-push” inflation. Most folk here are old enough to have experienced stagflation in the 70’s first hand.
Socaljim:
What about plain old fashion money printing press inflation?
Where central bankers are too lazy to bother printing money and get ink on their hands, instead preferring to create money out of thin air, since it is cleaner and greener! (I think central bankers have already met their zero emissions goal!)
Like anything that is free, there is unlimited demand for free money! Of course producers are only going to produce something if the price is higher since the money is worth less!
Another way to look at these two kinds of inflation as 1) money printing inflation caused by devaluation of the currency and 2) scarcity inflation due to running low on resources and energy. Oil, Iron ore, Trees for lumber, sand, etc. are not as easy to get as they used to be so things that are made from them become more costly, or just become unprofitable causing shortages. The problem with the second kind of inflation is that is causes dislocations in the economy that can be unexpected for some people. For example such inflation might make it seem that an exurban home on a big lot, might be a good store of value. But as scarcity continues things are cut back or become expensive. So that house in the exurbs costs too much in energy to get to, or maintenance expenses like replacing the roof become uneconomic.
In classical economics there is no such thing as demand side inflation. Because if there are no constraints on supply then supply rises to meet demand. So in a commodity with no supply constraints like digital downloads of the Beatles song “ When I’m 64” as many people can download it as they want and the price stays the same. But if more people want a thing, say 1959 Porsche 356 but the supply is constrained ( because they have not made them for 61 years) then price goes up. So while some may attribute inflation in house prices by the beach to demand, but the inflation is really caused by the shortage of beachside lots. To prove the point if California built sand spit islands off Newport Beach like they did in Dubai the supply would increase and prices would go down.
Demand side inflation is also called demand pull inflation.
Think Mother Nature is gonna kick neoclassical economics to the curb very shortly.
Cost push inflation only impacts new housing development. It doesnt impact sales of existing homes because they dont have a cost increase. And existing homes are the vast majority of the market.
No, this is fully a supply-demand imbalance that is rather short term, although it might linger through the end of the year.
The big key here is interest rates. They have been pushed as low as possible. Not going lower. Fed knows that negative rates are a real problem. Even more important than the interest rate is the trend in interest rates. So if you have a continually falling interest rate environment it keeps driving prices higher, year over year. As people see prices always higher, they want to buy as an investment. It sets up a psychology that is ingrained. When the reverse happens, people see that the asset price is falling and dont want to buy it. They demand a much better price to take on owning a highly leverage asset (assuming they buy with a mortgage). And in a falling price environment, people walk away from homes and turn the keys to the bank, who sells the home at a deep discount, further pushing prices lower.
The big question is whether the bank and real estate industry can lobby for some new financial laws that protect banks and prevent the next real estate melt-down.
Have no fear for mighty Casey is up at bat!
Demand side inflation is also called demand pull inflation.
What will cause (force) a housing price collapse to occur?
The only thing I can think of is if people lose their jobs en masse and US Government does not prop them up?
Interest rates going up will tank prices.
When 10 yr T Bonds went from 1.5 to 3.2% from 2016 to 2018, housing sales volumes started to tank.
And the stock mkt lost 20%.
After 20 yrs of interest rate repression, ZIRP is pretty much the only variable that matters anymore.
Not deal specifics or financial fundamentals.
May tank prices for cheap houses but not for more expensive houses that are bought with cash or lot of cash and a nice 3% mortgage, way below inflation rate.
And when prices drop, BlackRock and others will hoover up those houses for that wonderful reset where everybody rents and only a few own and conttol everything
There are a lot of black and white swans.
There is budget considerations due to inflation. The more a household has to allocate to other items than housing the less they can afford to dedicate to RE. Unless wages meet that increase, it’s a huge problem and that usually brings prices down. Also, increasing interest rates aren’t the only thing that causes this. It’s also increases in property taxes, rises in services, fuel, food, etc. Given rising inflation and already high debt levels this could be a real problem. We may have also already hit a debt wall where a sufficient # of the population can’t or wouldn’t be involved. Without sufficient #’s a mania can’t continue and may cause a drop to a collapse.
There is another pandemic, the current pandemic continuing, a war or other political instability, without the people’s belief/governments ability to continue backstopping the system, partially or fully. The system is built on a lot of faith.
It also appears that a lot of demand was pulled forward which means they might not have enough buyers to keep the prices at these levels. Nothing else is need to have a drop other than some people needing or really wanting to sell.
With the way people are responding to media reports, it potentially would only take the media saying “the market is tanking” and then it would become a reality. There is definitely a lot of that type of feedback loop going on in various parts of society and that includes RE. FOMO has begotten FOMO in part driven by the media reports.
The problem with using stats is that they are always checking in the review view mirror or put another way are a lag indicator. Watching the markets on a daily basis, I have been seeing the declining sales with reduced bidding wars and much smaller run up in prices. I’m also seeing price reductions that aren’t resulting in sales. All of this is only starting to show in the stats but it also suggest that we are maybe at the top of the curve and starting to slide down. So it maybe starting but it will take time to confirm and show in the #’s.
There also doesn’t have to be a “big” cause or force to make a crash happen especially after events like the last 10 months. There is still is no agreement on what has caused some of the past crashes. There doesn’t seem to be an “aha” moment involved. The market just stalled, started sliding and then went down the backside of a roller coaster on it’s own momentum.
Demand pulled forward? If those people were not getting free money, they would never have been able to afford that property in the first place. Creating demand is a far more apt description.
It’s going to be both. Those that had problem affording were able to and/or bit the bullet due to low interest rates and the pandemic. The panic due to the pandemic along with historically low interest rates created more demand.
Either way, all more households purchased than otherwise would have happened = demand pulled forward.
A real estate agent told me she just bought two houses because she didnt trust the stock market and wanted to own an asset due to all the inflation.
What people dont get is that inflation is the WORST thing for home prices. Higher core inflation means higher interest rates. That takes the punch bowl away from the party of home prices.
This is just naive investors who think that higher inflation means higher RE prices. The opposite is true. Higher inflation is the only thing that can truly stop the Fed from continuing to blow money into the economy.
Either the currency collapses and there isn’t enough money in the world to make me sell my house, or they keep printing money and the price of my house goes up slowly, or they shrink the supply of money, and everything loses value at about the rate of compression. The only thing that can hurt housing is some tech genius figures out how to do it for $10 a sq foot labor and material, with off grid solutions to the utilities, so you can live anywhere for almost nothing. Oh and you can work from home wherever you are. We almost have that one.
30 year mortgage is below the rate of inflation for the first time in 41 years. This will not end well.
For whom? For the mortgage holder it’s great?
Mortgage holders will be under water when rates normalize.
When will that be? 30 years from now?
You do mean ‘mortgage holders will have negative equity when their house value plummets back to earth’. We’ve been there before!
They don’t have to much higher, never mind historical norms, to collapse lots of households. The question isn’t if they will increase but by how much and when.
The number of active listings (May 2021) is about 50% lower than the number of active listings this time last year (NAR data).
It will for those who had their mortgage in 30 years, 1%, bonds! Danish national sport, is really converting mortgages, not soccer.
The real estate market moves slow. At some point those who have listed and not getting offers will lower their prices. This will start the price reversal trend. Also as days to sell increase this will be part of the reversal. When you start to see wide spread price cuts that will also signal the price reversal. If rates were to rise this would accelerate the process as would be buyers wont qualify for the loan size they need.
While I agree with you, one thing I am afraid will derail this whole thinking is the lack of FOOP (Fear of overpaying) in buyers, the counterbalance to FOMO mentality that dominates our society as of lately.
Say price do drop 5-10%….FOMO buyers in large might think it’s great deal to jump right back in especially with interest rate still staying low, basically putting a floor in any meaningful market correct/crash. As much as I hate it, it’s hard for me imagine this herd can turn in FOOP mobs. Buy the dip narrative is like gospel to the general public.
It happened eventually after the last housing bubble, but it took a while.
Anyway, you don’t need to waste time worrying about whether FOMO buyers will immediately pile in on a 5% drop–they absolutely will. The question none of us can answer is: will it be enough to stop the reversal?
I think we are still in the phase of stupid people overpaying for homes. First need to clear out those impatient souls. Then more houses on the market at peak prices start to sit a while. Then more inventory starts to erode pricing. Then home owners decide to sell before prices drop, then prices really start to drop, while at the same time foreclosures finally start again and no more forebearance. People think that tomorrow will be the same and today and make bad projections as a result.
Houses go to contract within days here in the suburban northeast. No slowing yet.
When I start seeing ‘new reduced price’ signs I’ll know we’re heading down.
There are prices being reduced in the north suburbs of Chicago. I saw one for 25k less but was probably overpriced to begin with.
Lisa,
A rendition of this that we agents are seeing in coastal CA is we don’t want to leave money on the table for our sellers by pricing too low and yet we don’t want to price too high and get no takers so…we hope for the best and try to price right with this moving target and if we overshoot, we quickly reduce the price. Typically, we then get multiple bids…which often drive the price back up. And to paraphrase Socal Jim who seems to know a thing or two about real estate, if a property has an incurable defect such as being on a really busy street, it may take awhile to sell but even those properties are eventually moving in this market.
Who would want to live in Chicago?
Another POS city run by democrats with a huge drug, crime, and education problem.
No problems like that here in Japan.
Reasonable cost housing can be found in many parts of Japan and regional areas such as here in Mito house are cheap compared to the US.
Shunji,
“Who would want to live in Chicago?”
2.7 million people live in the city of Chicago and nearly 10 million live in the Chicago metro. So some people want to live there.
Agree with you about Japan. Just one thing: how much money do you earn in Mito? That’s a rhetorical question; don’t answer it. The Japanese people I know in Japan are making a lot less than they would make in an equivalent job in the US.
I know an accounting professor who used to teach at the U of I in Champaign for a few years. He took a huge pay cut when he returned to a job at a university in Japan. But as you know, housing is a lot cheaper, and healthcare costs are very low (his wife has some health issues). So it worked out for him kind of. But the equation is not always straightforward.
About 8+ million ppl live in Chicago area. Why would anyone ask that question? You think people can just freely move around when they have families and jobs that keep them there? My husband is a teacher, and if he goes anywhere else he will make less. With the cost of living high everywhere, why move?
The city of Chicago is rad. Also it seems Lisa was referring to the suburbs north of Chicago which I’d think would include the North Shore (John Hughes country).
Who would want to live there? Lotsa people with means and plenty of choices.
Also, they obviously have a gang problem on the north shore as well. Uncle Buck’s niece’s boyfriend ‘Gnat’ was shady AF and clearly a drug kingpin.
Most of the Covid refugees that moved to rural areas will be desperate to return to urban comforts in a year, two at the most. But there will be no local people to buy their overpriced homesteads. That should have an interesting effect on rural property prices, as well as their ability to move back to the bright lights.
TT, that is when I will buy my mountain fortress in the boonies.
Watch that show Doomsday Preppers. Just wait till the old man dies and the wife and kids sell the “fortress”. Price includes a year of freeze dried food! Watch out for the hidden booby traps.
I like how the buffoons on that show tell you their names and approximately where they live.
I can go to the property appraiser’s website and figure out where they live in 2-3 mins usually.
Bunch of really bright people advertising where they stored their massive collection of guns, etc.
They leave for the monster truck show in the next town over and it won’t take long to clean ’em out.
I think this is true.
I have lot of friends who have school going kids. They want to stand in a good school district with lot of kids activities. I don’t think they’d move to rural areas.
They also don’t what their kids getting involved with gangs, so will continue to move to rural areas if they are from one of the many cities experiencing a crime wave.
If your kid joins a gang, you’re a really shitty parent.
And yes there are gangs in rural areas too.
How do I know this? Because I was born in a very, very small town in the South. If my choices were being burned to death or going back there to live…. I’d choose the fire.
Rural areas are geared to raising kids and have plenty of activities for them, in school and out. We lived in rural PA when our son was in grade school and he still remembers it fondly. He went to a gymnastic school staffed with Olympians, became a train hobbyist, had great day camp in the summers, and on and on. I had some of the best shopping too. The downside was the brutal winters.
I think (or maybe hope) that several trends will start happening in the next year:
– Regugees from temperate climes spend a summer in TX/FL or a winter in ID/MT decide it is not a long term living place for them
– those who romanticize living rural decide they miss immediacy of more dense environments. Similarly the suburbs can get very sterile for some.
– Things calm down a bit when schools start back to in person in the fall
– Workers realize that companies who start back in person with a hybrid model actually still require workers to live close (Apple purposely said Monday-Tuesday-Thursday, making a long commute impossible).
– Working from home wears thin for some people: those who realize serious advancement happens by being in person, those who get bored being at home all day, singles, those who decide being stuck at home with family 24-7 is not all that fun 24-7 after a year.
This is not to say trends will reverse, but things will calm down on the margins taking the froth off once things settle down in the fall and the newness of WFH wears off for some.
I hate working from home!
Making $100K+ w/benefits, never shaving, not getting dressed up (Wore an “Iron Maiden” t-shirt to work today…had to get dressed up for our weekly company meeting!).
I MISS not driving an hour to work (500 hrs/yr) every day.
I miss my annoying co-workers.
I miss road ragers/traffic tickets/accidents.
I hate taking a nap in my own bed on my lunch break.
Yeah, working from home is the WORST!
You’re right though…for those men who had to make a BUNCH of kids and who hate their wives and children….
Yeah, that would suck being stuck home all day w/those people you hate (your wife and children). #gopfamilyvalues
As for the rest of us….man, working from home has been the best thing ever….
1) A : New privately home units completed since Jan 2021 : 1328+1347+1497+1426+1368 = 7,000K units.
2) B : New one family single home sold since Jan 2021 : 993 (a peak)+823+886+817+ 769 = 4,300K.
3) In 2021 the completion rate is 60% of a decade ago, despite a larger population.
4) Home builders are more conservative than a decade ago. A is not equal
to B.
5) Many units are build for rent, not just to sell.
6) In 2000 the Nasdaq plunged 90%, but the completions dropped to 1.5M
units, which is today level, and in 2000 the CPI was three times larger, with higher mortgage rates.
7) A deep correction will send the 10Y yield to NR, and the mortgage rates to between zero% and 1.5%.
8) The Fed wants to avoid such scenarios.
9) The Fed created the scenario.
If you are a ruthless HR (catbert) the rush to working from home is a boon.
Every slacker, who has avoided taking on the extra tasks that being around colleagues in the workplace would have come their way, can now be replaced by someone with a young family and mountainous student dept.
A kid with a kid, hungry. Hungry and Prepared to be in the office for promotion like you were 10/20/30 years ago.
Good luck you newbie boondockers.
You’re f*cked.
It’s just a gully?
Some of the biggest national home builders like Toll Brothers and Lennar plat out the entire subdivision and get each house plan permitted and approved by building officials before they start selling. Then they take reservations for each preplanned house. When constructions is ready to begin they set the price and take a modest down payment from the customer. When the house is almost done (cabinets are in) they have the customer start the closing process and get a mortgage. From what I am seeing, a fair portion of the houses they have “presold” come back on the market because interest rates have gone up, or something else happens to keep the original customer from completing the sale. If the market continues to slow, this can cause a big unexpected unsold inventory to get built up in a short amount of time.
We also have all the vacant/2nd properties that haven’t been brought to market due to the vertical increase in home prices. Without those vertical prices those second properties are a very fast cash drain, a serious pain the the a** and a liability. If prices start looking weak, we could see some very panicked and desperate sellers.
We may also end up with more unexpected inventory when sold’s with very long possessions (we have a huge # of these) start failing to close due to falling price and failed financing.
Also, RE agents in various areas have told me that many of the urbanites that moved to the boondocks are trying to figure out what to do with themselves and having panic attacks due to the lack of social and retail opportunities. So can’t see many of them lasting much longer and that is even if they are still allowed to work remotely. In one neighbourhood we lived in, we took bets on whether these newcomers would move back to the city and that was before the pandemic mass exodus.
Which area of our fine nation are you referring to?
I assume you mean comments from RE agents. There are a number of spots in CDA, however, the most chatter has been coming from cottage country (Muskoka/Haliburtons/N. of Montreal) in Ontario and Quebec. Apparently, they really aren’t enjoying the winters snow or the summer aka black fly season on a full time basis.
I had breakfast this morning with a good friend of mine who is a pretty successful real estate agent and who also owns about 12 SFH’s (rentals) that he accumulated over the last 10 years or so. He said “things are slowing down”. This is Montgomery County, Texas.
He also said last year was nutty. But the selling and buying appears to be more normal now.
seasonally adjusted annual rate :
A : 7,000K : 5 = 1,400K/Y.
B : 4,300K: 5 = 860K/Y
What other Employee would still be in a job if they had acted in such an incompetent, reckless and Progressive way as the Fed for the last 25 years. Most people would be in prison for this sort of life-affecting behavioural carnage.
Tell that to the Deep State. They too have messed up this country with their grandiose plans for world domination.
Lol
Is that you Alex Jones?
You forgot to mention Q and the Bildebergers….
Polo here-
Ask yourself about the management that has run fortune 100 companies. M&A that quickly have to be shuffled off the books at the price of $50B, executive payment plans and golden parachutes, RIF entire divisions with what we would assume is no rhyme or reason, close entire segments of the business and have to layoff thousands, etc… This type of malevolent behavior is rewarded not punished.
Why is the FED any different? Oh, and who is going to stop them? Legislative , Executive or Judicial branch?
1) if in the next decade or two, the inflation rate
will be above the 10Y yield, above than mortgage rate, and higher than the annual rise of home prices and the RE yield, prices will drop in real terms, rise slightly in nominal terms.
2) In 2035/ 2045 home prices will catch up and jump > the CPI.
3) The best time to buy is when there is no more hope for pension seekers : not in saving accounts, neither in RE yield and definitely not in wall street.
3) In 2002/02 the RE market hardly move during the dotcom plunge.
4) 2007/ 2011 was : too deep.
5) 2020 hi/lo : too deep for 2 months, possibly a trading range for the next decade, or two.
6) A RE frog cooking will be delicious for the zoomers.
New home prices going up is good news. When this is trending down that usually indicates a recession is coming. The buying trend seems to be bigger houses, so the mix is skewed to higher priced homes. Nothing here looks crazy to me.
We had a wacky 18 months, so reading anything into current data is not a good idea.
Keepcalmeverythingisfine,
Price is the last index to change direction.
During the housing bust, sales of new hoses started dropping in late 2005. Prices began plateauing at that time through mid-2008, then began plunging. By that time, sales volume had totally collapsed and unsold inventories had become catastrophic. Prices didn’t bottom out until two years later (2010) and then stayed down for a couple more years.
During the 2005 housing bust the first thing to change was “days on the market”. Houses started sitting sometimes for months without selling. I noticed it around here back then in relatively good neighborhoods including mine. The next thing was some houses that were sitting for a long time switched to “For Rent”. Like Wolf said the prices leveled off as sellers refused to drop their prices. Then those that had to sell because of job changes lowered their prices and we saw a 20 to 30% decline in sale prices. Around here prices bottomed out in late 2009. So far I don’t see any of these things happening right now, so if you are holding your dry powder for a crash in prices you’ve got a long wait.
I noticed there was no mention of interest rates in your optimistic scenario.
Although I am POSITIVE it is another wolfertypo, in fact, the following , ”sales of new hoses ” was and is EXACTLY correct Mr. Richter…
Watching houses that had been selling for $20-30K going for 10 times that much a few years later, 05 being in the midst of it,,, some of the old timers in FL knew almost exactly what was happening and the eventual result there of, which did happen almost exactly.
???
Why do so many people think rising home prices are a good thing? FLAT home prices are a good thing….
– your property taxes don’t rise
– when you sell, your sales commission isn’t larger
– when you sell, you aren’t giving away a chunk of your value to cap gains taxes
– and then that means you don’t lose purchasing power when you move
Conversely, rising prices mean the opposite of this. In areas that rise a lot, and the owners have owned a long time, they can’t afford to buy the house they just sold. Picture someone at the coast, paid $300k in 1991, sells now for $3 mil. After taxes and commission, they have about $2 mil left. Obviously, they’d have to scale way down to a much lower level home or relocate someplace cheaper. Except now, in CA, in that 1/3 cheaper home, their taxes will be much, much higher than they were in the more expensive home.
And yes, I’m aware that the average home, and even well above it, doesn’t end up with a taxable cap gain (>$500k gain for a couple). But the numbers I quoted are common along the coast. Actually, in So Cal, they’re REALLY common now.
That’s what prop 19 was for last election and it passed. Boomers created this mess in 1978 with prop 13 and the only consequence to their fervent nimbyism to drive up their property values at the expense of the environment and society at large was that if they moved within CA, they had to pay the higher property taxes. They cried and complained about being trapped in their homes, unwilling to part with some of the money they’d make by selling their home. Now they can have their cake and eat it too! With some help from CAR and Newsom, prop 19 allows those 55+ to move anywhere in CA 3 times and keep their property tax assessment.
All I have to say is Californians love inequality and feudal hierarchies. Like the FED, they talk a good game about progressive ideas, yet keep implementing policies that do the opposite.
Quit already with the ”boomer” stuff h.
In ’78 the OLDEST boomers were 32, ( a few years younger than us War Babies ) and not many were doing all that much with politics, mostly still partying on dude! The so called ‘greatest’ generation were still very much in control of CA then, and were very happy to see that prop pass.
FL too voted in a property tax increase LIMIT, and most cities in that state also give additional help in the form of reduced assessments for elderly folks. Along with the lower sales taxes and no income tax, it provides an opportunity for middle class folks to finish out life with at least some possibility of making it to the grave without being on welfare after working for 50 or 60 years…
IMHO, that is a good thing, as I remember many old folks being driven out of their long term homes when someone overpaid for nearby lot and built a mega mansion, thus driving up the appraised value of all nearby homes.
As far as moving 3 times and keeping the tax advantage, IMO that actually helps younger buyers too, as older folks can now downsize to appropriate smaller homes, and many have done and will continue to do so.
Eastern Canada here.
No house on the market longer than 2 weeks. U-Haul trucks continuing to build up at local franchise – they’ve overflowed into a neighboring field now. Area population increased by 4% in one year, hospitals and schools overloaded. Since the majority of homes being bought are newbuilds with much higher property tax valuations than existing ones, the governments are happy. Same all over the region. Incomers give a wide range of reasons – WFH, retire early from more expensive areas, low crime. They all seem perfectly happy to give up the excitement of city life, which isn’t surprising given there hasn’t been any for a year. Personally, I think a diverse group of people suddenly getting the same “idea” at the same time probably has a single cause that they don’t want to talk about.
They are actors in A Fistful of Dollars, giving each other sideways glances, with The Unknown Stranger reluctant to say “Brunswick Sardines”
The majority of people don’t have a handle on nation’s finances. Average Homer Simpson is flush with cash, but consolidating government, corporate and personal balance sheet savings is at extremely low level around 2% last I saw.
People are taking on larger commitments but don’t realize future real growth rate is going to be slower.
I think that is one reason Fed wants inflation to run hot because real growth is low. If real growth is 1% they need to get inflation to 3% to keep nominal at 4%. But I think we are going to be like Japan and nominal will just keep driving lower.
We will be like Japan except for the high crime rates and lack of work ethic in the population. Plus, we will have more free money and social programs for those that choose not to work.
“lack of work ethic” = not wanting to slave away for 60+ hours a week to prop up a rotten economic/political system. only an idiot would work hard given the current incentives. we’ve never seen the old attempt to eat the young in such a way before. it’s sad
U-Hall for 19.95/d is rental co.
big money is buying real things folks. Currency collapse coming that’s what these rising prices signal.
It’s the end of the world as we know it!
It’s the end of the world as we know it!
It’s the end of the world as we know it!
And I feel fine!!!!
Hahahahahahahahahahaha!!!!!!!
Is Winter Coming?
Not anytime soon according to George R R Martin.
What could really be the next swan. What about the debt ceiling negotiations collapsing? Government shutdown 2021!?! Yellen says there is enough to keep funding through August if no deal is reached. This seems like the perfect storm. That will drive housing supply into the ground as nobody will be sure if they are getting a paycheck from the government
JPowell’s fat finger. One day he would just print 100 trillion because the Enter button got stuck and he keeps hammering it without waiting for confirmation to go through ;)
One option is we go down once more and Fed being stuck on the zero bound will try to do massive QE maybe $10 – 20 Trillion this time. Will market then go risk on or will it say system is done and go risk off?
In other words he will fill the banks with more money that they can’t find approved borrowers for. Still no velocity of money and GDP stalled.
Sorry Wolf and folks living in the US!
Hate to break it to you, but this” bubble “ is set for bigger and bigger expansion.
Once the immigration, legal or otherwise start to pickup , especially in the margins of the skills scale , the same immigration that wrecked havoc in other markets in Europe, Canada, Australia, the bubble will be marching on a long time for it to find its extremities.
There is acute skill shortages in technology, which is basically driving the NASDAQ and to a certain extent the DAW.
and Not everything can be done remotely as Wolf try hard to make us believe! :)
On the other side of the scale, jobs in low skilled agricultural, warehousing, and the likes are still scoffed at due to the “generous “ government’s teat that had the lower skilled labor hooked on free “ Manna”!
It is a hard task walking back the horrendous damage that the Government have done to the Economy of the country by the magnitude of failures in implementing a level- headed policies to counter and survive the “ pandemic “.
When you break a machine ( finely turned and fragile )as the economy generally is , you run the risk of rebuilding it from scratch!
The volatility seen now in the indices, which signals daily fluctuations on a whim shows without a doubt that the markets have lost its COMPASS .
The Compass that generally shows how the world economy at large will be heading is now a very damaged non conducive environment of fear, lack of trust and straight out accusations of malice.
The layers of bureaucratic hoards that lost contact with reality have managed to Stuff up things so badly, that the broken chains of supply and demand are being stretched to the limit and destroyed even further.
There is every likelihood that “ the hub of the world’s manufacturing “ centered in Asia, will be in for a long term RE-adjustment, as the purchasing power of the ( largely extended western economies) causes lower demand in the near future and into mid term as well.
Don’t be fooled by the ( appearance of higher demand running at a feverish hot sectors like construction and electronics).
This adjustment will see the short term prices for manufactured products rise sharply as they are now, leading to further unwanted damage and backlogs,
regardless of the current attempts to normalize economies ( after C19 fiasco).
The continuing talk of the need for further ( jabs) after the purported ( two jabs only adequate sell by the vaccine aficionados ) having an even worse effects on a population fed with the proverbial from the manufacturer of the “elixirs of life!!”.
It will take a radical change of direction from the government, a really sincere bipartisan approach to re orientate the Economy to serve the people it’s purportedly working for.
In summation, the banks should be forced to invest in the real economy rather than hoarding the dough printed by the government to earn their 0.05% from the FED. ( a clear attempt to feed the brotherhood!).
Without real tangible investments in the companies that manufacture or produce real things, this fiasco will continue until we reach the point of collapse, the collapse that Japan is still trying to push forward.
But can a leading economy with the world’s largest reserve currency manage the feat that The Japanese achieved?
Same comments week after week by same people.
Very tiring comment board.
they’re all retired with nothing better to do. what do you expect lol.
Apparently Wolf is holding a gun to your head to read the article and comments? No?
My suggestion is put in your thoughts so we all can get more enlightened.
Maybe start your own blog, and convince everyone to subscribe to it?
But then again, you’re not cut for that sort of headache.
Please do put your opinion on the housing market, or any other topic, so we might all benefit from your wisdom.
You mean like a daytime soap opera? Turn it off for 6 months and turn it back on and you haven’t missed anything?
Its time to consider moving the U.S. Capitol out of Washington D.C.
Reason: The weather is getting hotter and more awful every summer. I’ve noticed the change every year. Now that we are in June the sun is directly overhead beating down like a sunlamp 8 hours a day. All the building of concrete structures to house useless government agencies and contractors has not helped. Cutting down the tree canopy to built these concrete structures has caused a crypto climate change inside the Beltway. And don’t believe the government’s weather data. I’ve got my own weather measuring equipment. The reported temperatures at the Airport are bogus. My data shows the temperature are 5 to 10 degrees warmer than reported, and the humidity is off the charts. Everything the government puts out is a lie including the weather.
Well an overhead pedestrian crossing collapsed earlier today in Washington DC. Talk about the need for an infrastructure package. Knowing DC though …. it will be laden with pork and mostly benefit the 1%.
I looked at that bridge on streetview. There is collision damage to the underside of the main concrete girder visible approximately where the break occured, and I note a semi truck was involved in the collapse. It was therefore possibly due to another strike, and so nothing to do with poor maintenance.
But, as ever these days, we only get news if it fits a narrative, and there’s never any follow-up if the final conclusion contradicts the narrative.
That explains the crocodiles in the Potomac.
1) Side be side on the salt water coasts, and in the sweets of the middle ==>
2) A false positive bias : buy in 1991 @ $300K, sell in 2021 @ $3M, because the $ value plunged.
3) The boomers are cashing in, moving to FL, but Miami building
collapsed overnight, without warning.
Problem with real-estate is sellers are always looking backward. House prices have increased over the last year by xxx%, while buyers always look forward. House prices wont do very well next year as demand is now tapering and supply growing and interest rates climbing.
The full effects of “stimulus” I believe are very misunderstood and no ones to admit to errors.
No mention of Wildfires, I find that curious.
We’re in the middle of an extreme drought throughout the Southwest, we are going to lose homes this year.
At best it will be bad, at worst catastrophic.
If the Hayward/Rogers Creek Fault lets go early this October when the winds are gusting to 55MPH it will be “Katy Bar the Door”.
It’s going to be a long hot summer.
I noticed that too. There also isn’t any discussion on the knock effects from the drought that are looking increasingly likely.
A double wide in the east county of San Diego is listed at 399k. 1400-1600 sf homes in the middle of the city are selling for a mil or very close to it. Junk goes for 750k in half way decent hoods. The bad hoods are getting over 600k for 900 sf post war junkets. Last time i remember a frenzy like this was 15 years ago, but then there was inventory. Today there’s none. It’s only because of the no inventory that I don’t think we’re gonna see a bubble pop, at best a slow leak will develop but it won’t be enough to offset the pumping going into it, at least in San Diego county that’s what I see. Maybe in a few years as inventory increases it’ll be different.
You must have a Ready, Willing, & ABLE Buyer. We may run out of ABLE Buyers soon. The prices are too high.
I agree with your analysis. Hard to have a crash with low inventory. Slow leak maybe.
@Gomp – you are correct. You need a willing buyer. I think we will see willing buyers but it will be multi-generational buyers to afford new homes. This is not new. Prior to WW2 many multi-generations lived in a housing unit.
I think the trend of affordable housing for the lower 50% is going away. Corporations are becoming in essence monopolies (Amazon, Walmart, Home Depot). They pay many of their employees below living wages. I read close to 40% of Amazon and Walmart workers need entitlements (food stamps, etc) If you need food stamps then how can you ever buy a house.
I saw a double wide with a garage sell for over $300K, in Boise, Idaho. Absolutely nuts, the wages here cant support this.
Yeah, but saying these houses (and comparable assets like stocks/LT bonds) are worth 30% less puts the overall economy is a deep recession. The Fed has backed itself into a corner because it has no integrity or discipline.
The bubble pops when it has sucked in many people and most people believes it won’t pop.
Although the market in San Diego is still hot but I see it softening now.. homes coming back to market.. price reductions ( altho quite high to begin with )
I believe patience would be rewarded.
It will be difficult for housing to appreciate, now that we are at the zero bound after a 40-year down-cycle. The only thing keeping housing alive is deficit spending and money printing. Let’s see how that works.
I’ve never seen so much traffic in the Swamp over the last week. I’m longing for the days of the lockdown and the Covid-19 panic. Then you had all the roads to yourself. Now’s its back to the old Washington DC gridlock. Yesterday I got stuck on a main commercial strip near downtown and didn’t move an inch for almost 20 minutes inhaling Carbon monoxide. Its total insanity on the roads. We were rated by AAA as having the second worst drivers in the USA, Miami being the worst.