The brick-and-mortar meltdown for mall landlord started years before the Pandemic. For WPG, it started in 2016.
By Wolf Richter for WOLF STREET.
Washington Prime Group and certain of its subsidiaries filed for Chapter 11 bankruptcy protection on Sunday, the third publicly-traded mall landlord in the US to file for bankruptcy in eight months, following the bankruptcy filings of CBL & Associates Properties and Pennsylvania Real Estate Investment Trust in November 2020.
The bankruptcy filing had long been in the cards. The company, in its announcement, blames the Pandemic, but the difficulties of the Pandemic just pushed the REIT, which had already been teetering, off the cliff.
Back in May 2014, when Simon Property Group [SPG], the largest mall REIT in the US, spun off Washington Prime Group, its shares [WPG] were initially trading in the $190 range, and for the suckers that bought them early and held on to them, it has been one heck of a punishment, as those shares have relentlessly dropped, interrupted only by false-hope sucker rallies. By February 2020, before the Pandemic plunge began, the shares were trading in the $25 range, down 87% from their early days. Now they’re down about 98% (data via YCharts):
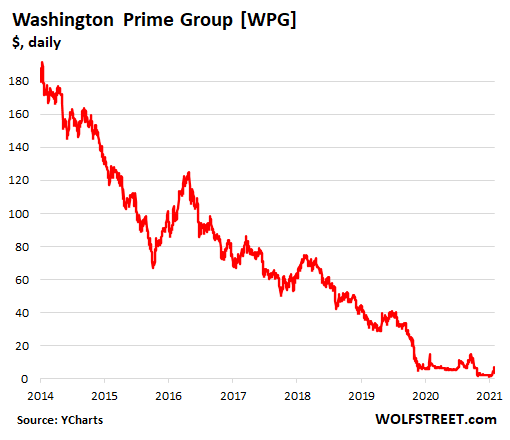
In terms of revenues, the year 2015, the first full year as independent company, was the peak year, at $922 million. Revenues then declined every year. By 2019, they’d dropped by 29% to $656 million. In 2020, they plunged another 25% to $491 million.
Today, Washington Prime Group’s shares plunged around 50% when they opened, trading in the $2 neighborhood, but have bounced off those lows. In May, they’d already traded at this level, but in early June “spiked” again, to nearly $6 by June 9. That mini spike has now mostly been unwound.
This has been the long and methodical process of the brick-and-mortal retail meltdown, as department stores collapsed and disappeared, and as surviving department store chains shuttered innumerable stores. Department stores are the anchor stores that pull in foot-traffic at malls, and when they close, the rest of the mall is in real trouble. Mall landlords – and their creditors – take the hit. And with Washington Prime Group, Simon was able to spin off its weakest malls.
This was a prepackaged bankruptcy filing. Washington Prime Group said in the announcement that it had executed a restructuring support agreement (RSA) with its creditors, led by SVPGlobal, a PE firm that specializes in distressed debt, and which had bought a portion of the debt at big discounts to face value.
These “Consenting Creditors” hold about 73% of the principal amount outstanding of the secured corporate debt and 67% of the principal amount outstanding of the unsecured notes. The company listed $3.4 billion in total short-term and long-term debt on its balance sheet at the end of Q1.
To fund operations through the bankruptcy process, the company has obtained a $100-million “debtor-in-possession” (DIP) loan. The agreement with the Consenting Creditors includes provisions that would reduce the company’s debt by nearly $1 billion; and it includes the possibility of a $325 million equity rights offering.
During the bankruptcy proceedings, the company expects to continue operating its malls “in the ordinary course for the benefit of our guests, tenants, vendors, stakeholders and colleagues.”
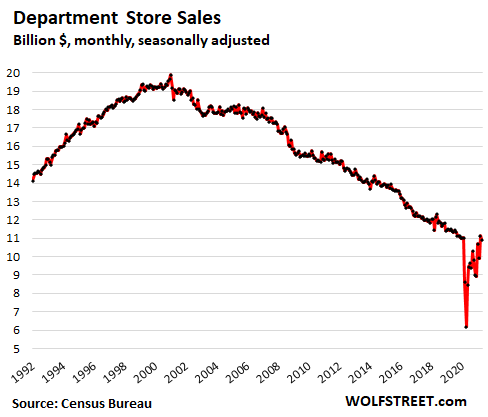
This is what all malls face: The collapse of their anchor stores as brick-and-mortar department store sales have been on an irreversible trend to oblivion that has been going on for two decades, as ecommerce has taken over their business.
Some department store chains have been able to build up their ecommerce divisions, and now have a vibrant ecommerce and fulfillment business, and their ecommerce sales are an ever larger portion of their total sales, as their sales at brick-and-mortar stores have spiraled down, amid the structural change in how Americans buy the merchandise that department stores offer:
Enjoy reading WOLF STREET and want to support it? You can donate. I appreciate it immensely. Click on the mug to find out how:
![]()


Aside from all the sugar daddy money…..the banks have to be stuffed with lots of bad paper. Real estate is one of their largest lending targets…..and quite a bit is either suffering low occupancy or low demand.
They better have lots of treasuries….they’ll need it to survive the debacle coming when recognition and mark to market hits.
why isn’t simon group on hook as secured borrower
Buying opportunity for the taxpayers, via the private bank owned Federal Reserve.
It’ll be a private profit/public debt partnership. That’s what makes America great!
The price of lumber is down about 40%. The price of mall stock deflated too. Might convert malls to condos or fulfillment centers. Amazon is growing. Bought a bicycle from Amazon last Tuesday. It was delivered Saturday.
Glad somebody mentioned lumber’s turn back toward something resembling sanity.
This particular period reminds me a bit of the 2008-10 commodities frenzy, when financial players knew DC was going to have to disembowel the dollar, so they rushed into real assets (including foods – creating a LDN food inflation crisis).
Here we are again.
Great job DC.
I was told OSB around here is 60 bucks a sheet. I was just talking to area salesman. He said with 30 years of doing it, 18 bucks was the high, until now. He said lumber is coming down, but not OSB and other wood products…
Plywood sheathing is down in BC, as well as dimension lumber. If you want further lumber price declines petition DC pols to remove the current18% tarriff on Cdn milled lumber products. 18% to protect a moribund domestic industry for political purposes is pretty dumb in an era of high prices. If a domestic producer can’t make it in times of extreme demand, what’s the point of consumers paying for life support at the till?
“There is only IBM and ITT and AT&T and DuPont, Dow, Union Carbide, and Exxon. Those are the nations of the world today” And Simon Property Group. RIP Ned Beatty.
Network. great movie. also Rollerball (1975 ) was prophetic
That movie rocks!
Jon-a-than!
IBM has the wisdom to stay up-market, diversify upmarket, & spread itself around .. 170 countries .. someone is awake at IBM.
IBM is not upmarket, they’re basically an Indian operation whose major focus is buying back their stock to impress Wall Street’s short-term focus, cutting corners to cut costs and moribund legacy systems. I won’t mention their nickname here but it is not complimentary.
Mike G hit the nail on the head. IBM has been circling the drain for about a decade now.
Great actor!
Network…..an amazing and prescient film!
Backs up wolf’s point about how demographic changes in society are drawn out and not and overnight phenomenon and are intellectually lazy to use as excuses for rapidly developed trends.
Brick and mortar has been dying slowly because shopping habits and demographics have changed. I seen clickbait crap saying millennials are entering their prime home buying years… As of 2 months ago. Millennials are changing the demographics overnight and suddenly millennials are the largest demographic group in American history. I’d have to look at the numbers but I thought our population was slowing rapidly. Would post WWII baby boomers be the biggest demographic of home buyers? The previous clickbait article said millennials are living at home with mom and dad permanently and never moving out and being no good leeches destroying the “career” that is real estate agent.
I think America is shopped out.
I don’t know any of my friends that will spend an entire day at the mall shopping.
My mother’s generation seemed to do that at least once a month.
Our mall is chock full on the weekends. I don’t know if it’s a social event or people just going for the food court. But it’s 98 F outside most of the summer and mall walking/gathering is better than being outside.
But are they buying?
Trucker guy,
Read recently half our population born 1981. I believe it.
Peak population growth was reached in 1968.
Since then the population has slowed.
It is estimated that the world population reached 1 billion in 1804.
Apparently, within the 217 years from then till now the population of the world grew to the accepted figure of 7.6 billion.
I don’t believe it .. how did man manage it .. what with all the wars & pandemics & starvation.
A pertinent question to ask may be “Exactly how many of us are left today?”
The Washington Post .. Richard Dawkins (in an attempt to draw attention to himself) “aside from the moral problems, eugenics would work in practice.
Last year11,000 scientists signed a statement urging population control to save our fragile planet. Alarmists at work.?
Before we go any further we need to demand a head count.
Population growth of a little over 1% a year can explain 8 times as many people in 217 years. The ‘magic’ of compound growth rates.
The figure would actually be around 8.6 Billion.
Technically the Millennials are the largest generation in history, as most of them were offspring of the previously largest generation in history, the Baby Boomers. However, unlike the Boomers who often had numerous siblings, the Millennials often had only one sibling or were only children, so while the sheer number of Millennials exceed those of the Boomers, the rate of Millennials per parent was significantly lower.
Millenials are the pride and joy of GenX,of which I am.If they have boomer parents,then they be old as first time parents!! :-) Regarding pop control,we need to start with the greedy so called elite ad They are sucking up resources left and right,polluting like xrazy while admonishing those plebes barely surviving to,”Eat less meat and stop having kids you are cramping our luxury island life!!”
Might as well copy and paste this for what is coming in 2021.
“and for the suckers that bought them early and held on to them, it has been one heck of a punishment, as those shares have relentlessly dropped, interrupted only by false-hope sucker rallies.”
So…it’s a buy now with the meme stock strategy?
“Washington Prime Group and certain of its subsidiaries filed for Chapter 11 bankruptcy protection on Sunday”
Yeah, that kinda happened intraday.
Wolf! I know your strength is in motor vehicles, but you have a gift for triggering responses across the board. Makes you one of the best commentators in this environment. Thanks!
You kinda have to feel sorry for the mall owners. When the big department stores started to fade as top notch draws to the mall they figured they could compensate by bringing in the ultimate crowd draw–(drum roll please) movie theaters. That plus video rental stores and CD stores and nothing could go wrong.
Taxpayer funded or guaranteed?
“To fund operations through the bankruptcy process, the company has obtained a $100-million “debtor-in-possession” (DIP) loan.”
Neither. DIP loans are standard in bankruptcy proceedings. They generally get moved to the top of the capital structure under the supervision of the court. So DIP lenders would be the last to take a loss. If it looks too risky, they don’t do it, and then the company cannot be taken through a restructuring because it doesn’t have operating funds. Instead, it will be liquidated.
–> Costco and TJMaxx enters the chat.
“This has been the long and methodical process of the brick-and-mortal retail meltdown…”
1) UST10Y = 1.5%. // inflation expectation for the next 3Y = 3.6%.
That’s not high in comparison to the 70’s and the early 2000’s.
2) Prices today will be close to prices in 3 years, if the bubble cont
until 2024.
3) In the 70’s, during the high inflation period, RE prices fell less,
because the high inflation supported & lifted nominal prices.
4) In real terms the RE bust was much deeper.
5) During low inflation period, the gap between nominal and real prices
will be small.
6) Therefor the next bust will be deep and painful.
7) More people in own RE than stocks.
8) The deeper the bust, the higher the unemployment will be.
9) The Fed might “fix” it with NR, like Japan.
‘ The Fed might “fix” it with NR, like Japan’
But Banks won’t like it!
Fed is owned by Banks!
NR will destroy the dollar
LoL- this was a slimy bit of strategy to save Simon, and sucker inwestors up into their eyeballs.
And it worked for a while…
oF COURSE, no recourse to Simon says…
“this was a slimy bit of strategy to save Simon”
Kinda got that vibe too…in these situations you always gave to make sure good/viable assets aren’t being segregated away from bad/unviable assets, with the latter being marketed to the public
Simon says … there is always a sucker available when you need one!
From mall rats galore .. to mall reits abys($)mal, in just a decade.
Your post, Wolf, conjured up a sort of cartoon visage; of precariously stacked reeking and creeking mall units, resting on a bed of marbles .. as a teensy-tiny pointed object give the whole lot a jab, uhh, ‘forward’!
We have here, in our small city, a general merchandiser (not of a chain), that does a booming business, in spite of it all. It is a co-op of sorts,is tot fancy, but carries much of what the community prefers, and/or needs. My intuition tells me that e-commerce will lose some of it’s shine, not only due to people actually wanting to see/touch/examine what they may intend to own, before purchase .. but also because of the always increasing intrusiveness on to the public, by the Corps – At .GoVs behest – ALL for a quatloo.. completely crapifying what made the internet experiance such an empowering thing for the plebes. Now, for the most part, it’s just become an onerous financial mycelium of crony, corrupt Corps./.Gov increasingly calling the shots .. to be crapified even further because of energy/power constraints mixing things up ..
hello polecat.. just do us a favor and just keep the light on in the back office by the men’s room, the one behind the Food Court – for Paul Blart (Mall Cop) and wife Amy. He likes his job.
ah, polecat! i actually wondered when and where that’d happen because as i’ve mentioned here, it’s absurd that you cannot get what you need locally at all anymore, and after running around trying to buy things in Real Life, you have to order online little things that used to be at hardware stores, pharmacies, clothing, sports, or electronics shops. but now the quality declines so quickly, what you got 2 months earlier is now dreck and many, like my neighbor, toss away mis-represented items and crap, rather than deal witih return hassles.
i wondered when someone would return to the idea of a general store again. AND a co-operative of sorts? fascinating, because this is what our own PETUNIA was saying should be the wave of the future regarding cooperative business spaces for multiple stores/businesses.
this is a good sign. a very good sign that some are finding a secret cul-de-sac somewhere under the crusty rim of this glassy smooth toilet bowl, from the whirpool action of this economic toilet flushing everything down.
another good sign is that my favorite DJ X1 on KPOO is doing Juneteenth on his own at the park without permission from the city or his own radio station. / and i was just gonna dance it out to another DJ on saturday morning (if he’d do it live now that i broke our secret of me dancing outside to his mixes on the air).
x
In the local strip center by my house someone just opened an Amazon returns shop.
They buy their merchandise by the pallet sight unseen, so there always always random products and clothes to look thru.
I can see these becoming successful around the country.
A funny gadget was left at the front door with someone else’s name on it.
WTF
Several weeks later there was a knock at the door
“I didn’t order it, sorry .. please wait for a moment & I brought out the other one .. “No don’t give it to me, I can’t take it.” “Yes you can, thankyou” & I shut the door.
Dear Mr Harrold-
there will always be the junk peddlar on the street, on craigslist, on ebay, working out of their cramped storage unit, apartment, or in a building. and the idea of forthcoming chains of cheap Chinese crap no one ordered next to thrift stores and discount chains sounds like a future toilet backup and overflow, and not a creative way of hiding our soiled tissues.
but in the midst of the massive toilet of our predicament flushing everything down (if only we could return to the quaint times of simply not throwing out cute babies in bathwater), i’m looking for the proverbial “seven generation-ish” (the new me would settle for us just looking ONE generation ahead instead of up to next week), i’m looking not for new creative junk shops or more middle men apps taking cuts of everything, but i’m scoping out for long-game creative collectively grounded COUNTER MOVES against all this nonsensical wasteful short-term thinking.
that is where i will put my attention and that’s why i’m here on this very site.
i was also born in Manhattan (Spanish Harlem, though), and i’m comfortable with being different, special, outcast, and not play in their sheep games. i’ll be the one rogue rabid mad sheep with matted hair, willing to be cut up vintage couture dresses than non-Manhattan people would SELL to make payments on cheap crap they accepted from amazon.
you can’t take The City out of the girl so i’m still different enough to make a ruckus and find my Crazy Sheep Soul Tribe trying to make a run for it.
for what??? Another Way. i’m still trying to decipher my way past the distractions and propaganda so’s i can ask the right QUESTIONS as Unamused said before he went POOF! and disappeared. /for now.
x
Rats fleeing a sinking mall. That’s how far we’ve come.
tot > ‘not’
sigh
I do not think we are anywhere near seeing how bad this is going to get. The damage that has been done will have effects well into the future.
There has been so much wealth destroyed over the past 2 years that I do not see any way it will be recovered, in the foreseeable future.
Between the lock downs, shortages, and now near double digit inflation, it has been catastrophic for business. Some estimates are saying between 40% and 70% of small businesses either have not, or will not survive. It is likely many of the ones who are just hanging in there, will eventually lose confidence in things getting better and give up.
This may not mean anything .. Last week for the first time the delivery slots for Coles online shopping had next day delivery time slots available.
Great point, Jdog! Having a competent national response to Covid-19 would have helped save the economy and probably 400K lives. What we had instead was the action of Covid Don:
1) Call Covid-19 a “hoax” in public (not what he says to reporter Carl Bernstein who told him the interview was being recorded).
2) Says it will ‘magically go away some day’
3) Politicizes wearing the mask
4) Defunds the Cabinet level Pandemic Response team
5) Defunds the CDS folks we had station in China
6) Ignores the “Pandemic Playbook” (aka “Pandemics for Dummies)
7) I could list 100 other stupid, counter-productive and asinine things, but to what point?
The GQP and their Kult Leader are immune from logic and facts.
Thanks for pointing that out Jdog!!
No question the initial Federal response let by T was disastrous.
But that was the first 6 weeks or so. After that, the rapid development and deployment of vaccination was exemplary, far better than the EU as a counterpoint.
And it’s now very clear that some of the measures taken in response to the Federal laxity has been extremely counterproductive, the overall death rates in large blue states like CA aren’t noticeably different from TX and FL, and the schools still aren’t open in much of CA 16 months later with very clear science showing that school in person is both safe and far better for children in terms of mental health and learning. In fact, a pretty solid case can be made that the overall public good is being better served now in TX than in CA, and has been since at least Thanksgiving.
Depends what wealth is defined as. We’ve been destroying the resources we need to survive for many centuries now.
Jdog,
Some of the reports about the closing of small businesses don’t understand how small businesses operate. So if a restaurant shuts down, leaves the premise, and then four months later reopens at a new location, with lower rent, and the same employees, the restaurant owner may be better off. The hit was taken by the landlord. A lot of these small businesses shut down only temporarily.
You can see that because bankruptcy filings are way way down.
The damage I see in San Francisco are retail stores. But that is brick-and-mortar retail, and shuttered stores started being a problem years ago, to where the city council passed fees on landlords for empty stores. Because they were such an eyesore. The problem was high rents that small retail operators couldn’t afford. It’s just math.
Wall Street will fill the gaps replacing SBs with franchises. The gap between lost private businesses and new corporate businesses will allow for some inflation, but the process is always cost reducing, and should ultimately drive yields back down, (corporates are already taking the lead?) For the business owners they become managers make a good salary and without the worries. Part of this rollout requires infrastructure, whether its highways for delivery trucks or internet service. The first wave of corporate franchises made America ugly, and people resisted, but the second wave will be seamless and with more delivery options they can operate behind anonymous fronts. Not sure if this isn’t one way malls can re purpose.
Nearly every place I used to shop at is now closed. There is a stretch of retail businesses along Rockville Pike in affluent Montgomery County, MD where nearly every business is boarded up. Anyone that says we are in a great recovery is full of BS.
I haven’t been to a mall in over 3 years and don’t intent to go to one. There’s nothing in there that I want or need. Just imported Chinese clothing and junk for teenagers. I hope they all go bankrupt.
Most outdated business model in existence
I think there is light at the end of the tunnel for malls. The way the Fed is debasing the currency , the only way people will be able to meet their needs is through barter. These malls will become old time Bazaars with people trading chickens for cooking pots and turnips for plumbing parts. Barter is the Achilles heel of shop from home and the Amazon trucks will fade away with the value of the currency.
I would love to see malls turning into big flea markets with used stuff, because these are actually good fun to shop at. People reselling their Amazon junk when they are fed up with it.
When I was a primary school kid, I used to sell surplus stuff at a flea market that was organised once per month in our town. I collected toys that my siblings didn’t want anymore, sold them at the flea market and shared the profits with them. Also kitchenware, books, anything my parents didn’t need anymore. I liked to shop there too and it was always packed with people.
In the past, it was normal that when you went to live on your own, you started with stuff that your parents didn’t need anymore. Old couch, table, kitchenware etc. I still have much of this today. That even includes a ~1980 model vacuum cleaner that still works!
Even leaving the mall mkt aside, once REITS got their own subsector of the SP 500 (hiking demand for pure play RE ETFs) you could tell something was up.
Corporations had a pretty good sense that a lot of RE assets were overvalued and therefore it was a pretty good time to spin them off to a dopey public.
Now, if a lot of bonds and bank loans must written of, do not that deflate the amount of money?
If so we are in the interesting time that after a long period of monetary inflation without much consumer price index inflation, there is a switch to low monetary inflation, maybe even deflation, and high CPI inflation.
Yes, that is what I see coming too: asset DEflation combined with relatively high CPI inflation. Counterparty risk is going to be a prominent feature. This should also compress P/E ratios.
A couple of years back I shorted SPG knowing full well that given (1) an over-valued mall REIT market and (2) the demise of brick and mortar retail that that short was a good bet. But alas in this everything bubble the value of SPG went up and not down proving to me the futility of shorting this insane market. A lesson learned.
REIT spinoff = 5%+ chance of bankruptcy. It’s just baked into the REIT spinoff cake. This is what happens when you try to salvage the unsalvageable.
I love retail shopping but there is no reason for any chain store to have more than one location per city/town. The saturation is what destroys the experience and leads to cost cutting and low quality.
The luxury stores have few locations, by contrast, and much more pricing power. It’s not so much the exclusivity that’s the draw, it’s the curation of the merchandise that makes it interesting.
Some of the best shopping I came across was in PA. The small town boutiques, who didn’t sell enough to carry big labels, sought out merchandise from smaller designers in CA and elsewhere. Bought some great items that I still wear. Miss finding new and interesting stuff. Now everybody owns Rolex, Chanel, Louis Vuitton, …
Never can forget in San Francisco there were Starbucks on opposite corners of one of the main streets. You could order a Starbucks while looking at the other one. Burned into my memory
I used to work to work in this building in downtown SF where there’s a Starbucks on every side of it.
Here is another Starbucks story for you. There used to be a Starbucks on the Main Floor of the Excalibur Casino in Vegas and another one on the second floor in the food court. The escalator to the food court was about 40 feet from the Starbucks on the main floor.
Part of the problem may be that the chain signed a 10-year lease 8 years ago and then a larger location across the street becomes available, and so they take it and get it going, and two years later, when the 10-year lease of the old store expires, they close the old store.
Rolex, Chanel….you mean those products sold at the pub from behind the black raincoat? I once saw a shirt that had both Nike and Adidas on he front side. Rolex watches that rust. :-)
I can remember flying in rich couples to luxury fishing resorts. I had a blast mispronouncing the luggage names. I would say, “These Gottchee bags are really niiice”. Their faces would darken……..
It’s like finding a treasure chest.
If you want to feel sick, try counting how many McDonalds there are in your town.
Miss Petunia-
that’s the other reason i should’ve known you were from Manhattan; you’re actually into looking different. that’s why you like cutting up your couture dresses and being different NOW. but with the magic phones few want to look different anymore.
x
KL,
The standardization of fashion through branding is turning off a lot of people. In China and Japan, where brands are worshiped, many are going back to traditional forms of dress to break with the branding mania.
My love of fashion and lack of money started me on the path to what they now call high low dressing, pairing expensive items with cheap ones. I turned this into an art form in my personal life, but while you can achieve some really nice looks doing this, quality is always the best buy.
I am now cutting the heels down on my designer shoes because I am just to old to do high heels anymore. And the long sleeves on my old designer tees look like they are also goners. My contribution to the green(really broke) movement.
YOU are art, Petunia.
you’re living it.
but yes… you’ve also laid out my JOB as an artist stepping up to my job to pitch our individuality, humanity, spontaneity, and playfulness BACK to a society, culture, civilization that needs art to twist our heads to another direction and make it look good.
that’s the key to selling anything, right? but how do you sell people THEMSELVES and something they need that they already have within them?
this is waaaay outta my lane, beyond my pay grade, whatever cliche you wanna use, it’s BIBLICAL at this point.
how do you cut down HIGH HEELS and still wear ’em???
YOU are art incarnate, Miss Petunia. i cannot wait to meet you and see your closet on you.
xx
i feel you on the high heels; i’ve already given my platform whore shoes away to the kids or the Chicana across the street my age who would SELL her vintage couture if she had any because she sells used “whore gear” online now.
i offered to make her custom stuff because i wanted an older model our own age but she turned me down. James said it’s because she wants store stuff and wouldn’t want to be
DIFFERENT. i realized that was the new problem nowadays, but i agree with you that it will change because it kinda has to. it’s how things go.
but i didn’t want to get rid of all my timberlands because even the little short heel in the back is bad for my knee now. but i figured the front would tilt UP like clown timbs, so they just sit there.
and yes, my other late wild gay uncle who lived in sprawling flats with lovers in Manhattan, he used to bring me fashion mags and nice couture clothes/shoes from the trash area left in his building basements, and teach me what you said. mix something well made with …something “off” cheap plastic cute nasty or wild or intimate to keep yourself special, have ATTITUDE. not take all this too seriously.
he also taught me not to meet a man in full make up. washed and scrubbed natural. do the glam LATER because you don’t wanna look otherworldly and glam then have to surprise him in a bad way LATER.
that’s why Tammy Faye Baker went to sleep in full makeup. the stress of discovery’s too much; start out with nothing but full disclosure, fine print, or at least a tantrum or two.
it’s a different approach that i use in everything: show your worst ugly sides NOW and get all the shock out of the way up front so you can relax and spoil them later with the BEST stuff because they stuck around and proved they DESERVE even BETTER stuff now.
x
Where is the end effect of these bancruptcies on the CMBS mkt? Who is holding the bag?
Is Fed absorbing all the losses? Mkts are, as if, NOTHING matters! What am I missing?
A little perspective helps; these aren’t exact numbers but the total value of CMBS outstanding debt is over 800 Billion, something like 100,000 properties. This debt is held by institutions, and is sold in rated tranches. While there are currently 1000 retail properties in payment default, the vast majority of the retail dollar value in default is related to malls, while neighborhood and strip centers are at 6% overall default rate. The mall debt in default is about 11 Billion, a big number of course, and there is a universe of mall CMBS debt that is around 51 Billion.
Still, this amount of loss related to this debt is not enough to create system failures for the debt holders. Not all that debt is going to zero, some of the best malls will continue to develop into multi use high quality properties.
Outside of the mall business the demand for good retail is currently strong. We are seeing strong demand from both tenants and investors. We are in an early open state and nearly all of the Covid relief is in the rear view mirror. Values are higher as interest rates have fallen.
Currently the biggest challenge in the commercial real estate market is rising costs, not lack of demand. An incredible amount of multi family and industrial is being built, and single tenant retail users are buying land and building at a faster pace than pre covid.
A year ago many in the industry thought we would be seeing distress properties come to the market. Generally, this did not happen. However, for those that did get behind in payments, CMBS problem loans don’t get resolved easily. There are giant pre payment penalties that make it difficult to refinance and re invest in a property. So they can’t take advantage of the lower interest rates to try to remedy vacancy issues. They are also notorious for being difficult to work with, whether for an assignment or even a simple lease approval.
I expect that this will go on for years with the mall properties.
Although it was down considerably today WpG closed far above zero at 3.3.
How does a chap11 company trade at such a price
Hey I’ve seen people on WSB bragging that the Hertz stock they bought in bankruptcy is paying out at something like $7 per share which turned a tidy profit for them.
Maybe “Initial Bankruptcy Offerings” will be considered prudent investments in the weird future.
Is there a way to gamma squeeze this and make some money. asking for my friend.
“brick-and-mortal” – typo or deliberate?
And yet Simon Property Group has survived. Ok, they dumped their trash into Washington Prime but so what? Smart move. SPG sports a 4% dividend. It was suffering from the dwindles well before the pandemic, the pandemic hammered it, but look at the 1-year performance.
SPG survived the darkest days of the pandemic. They had no property tax relief and a depressed number of days open.
Although the possibilities for transforming malls has been discussed here and routinely shot down, apparently SPG didn’t get the memo.
They plan to reinvent their malls – at least some – by adding hotels, gyms, restaurants, multifamily housing, clinics, churches, and grocery stores. Communities in a box, so to speak.
I’ve been skeptical due to the perceived cost, but obviously SPG has a different perspective. They’re going ahead with repurposing their property. They’ve already done this in Atlanta, Seattle, and SoCal.
SPG is also talking to Amazon about converting defunct department stores into fulfillment centers.
Something to think about.
Simon is going to become the poster child for survivorship bias.
A decade from now they might be the only shopping mall REIT left.
Michael Gorback,
Yes, very smart move by Simon. Took a lot of pressure off them. They too are facing the same issues, and Simon himself has talked at length about it. They’re not escaping the trends. They’re just in a better position to deal with them, and they’re very good, as the spinoff has shown.
Simon has already returned a bunch of malls back to the lenders to let them worry about it — jingle mail.
Brookfield (#2 retail landlord in the US) is converting the biggest part of the Stonestown Galleria shopping center in San Francisco into something like 3,000 housing units. The remainder is getting converted — big grocery store, a multiplex that is already there (good luck with that one), and a new “Main Street” shopping and restaurant street that goes through the property. Building housing on these properties is the way to go in expensive areas.
Simon did have huge advantages in that their tenants were given tons of money, indirectly, from the government via stimulus for their customers. They were able to keep paying rent at their closed stores because of a surge in online goods buying caused by the stimulus.
I don’t know the specific numbers, however.
Three of our very large malls are now being repurposed as communities in a box. They will change over in stages, first being apartments or condos as it’s faster and has good cash flow due to high housing demand in the area.