Already troubled asset classes, such as student housing and student housing CMBS, face turmoil.
By Wolf Richter for WOLF STREET.
The pandemic threw higher education into chaos in the middle of the spring semester. How this will pan out for students, colleges, the whole army of people that works in higher education, the asset class of student housing, student housing mortgages packaged into commercial mortgage backed securities (CMBS), text-book publishers, and the rest of the industries surrounding the sector is highly uncertain. But even before the crisis hit, before the shutdowns, student enrollment in the spring 2020 fell for the ninth year in a row.
The number of post-secondary students – undergraduate and graduate students – fell 0.5% from the Spring semester last year, or by over 83,800 students to 17.18 million students, according to the Current Term Enrollment Estimates Report by the National Student Clearinghouse Research Center, released on Tuesday. Compared to the spring semester in 2011, enrollment is now down by 10.6%, or by 2.03 million students:
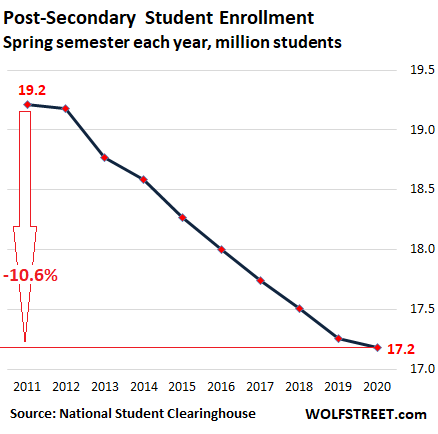
The Clearinghouse emphasized that based on the cutoff date for the submission of the data, “the current report should be viewed as a pre-shutdown, start-of-term baseline that does not reflect any effects of the pandemic on enrollments.”
The report is based on enrollment data submitted to the Clearinghouse by educational institutions (not survey based) and covers 97% of total enrollment of degree-granting institutions in the US. Since the data is submitted at the student level, it is apparent when students are enrolled in more than one institution, and those duplications are removed from the data, to generate the “unduplicated student headcount” in the chart above. International students, accounting for close to 5% of total enrollment, have been excluded from the student headcount.
All types of colleges were hit by enrollment declines.
This spring semester, compared to spring 2019, enrollment declined in all institution sectors. The largest percentage drop was at public two-year colleges:
- Public two-year: -2.3%
- Private for-profit four-year: -1.9%
- Private nonprofit four-year: -0.7%
- Public four-year: -0.6%
Enrollment in private for-profit colleges has collapsed since 2011.
After a long series of scandals, the government’s response to those scandals, and innumerable lawsuits filed by shafted students and others, enrollment in private for-profit four-year colleges has plunged by 55.2% in nine years, from 1.63 million students in the spring semester of 2011 to 729,364 students this spring semester – accounting for 44% of the drop in total enrollment in all types of institutions since 2011:
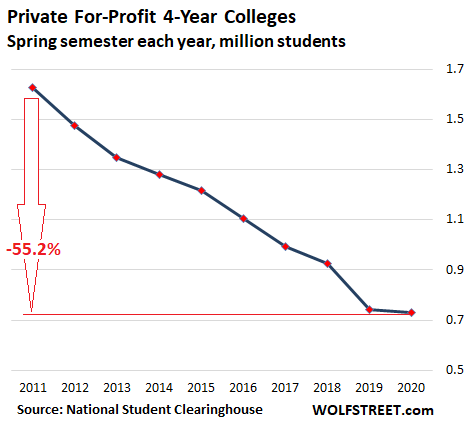
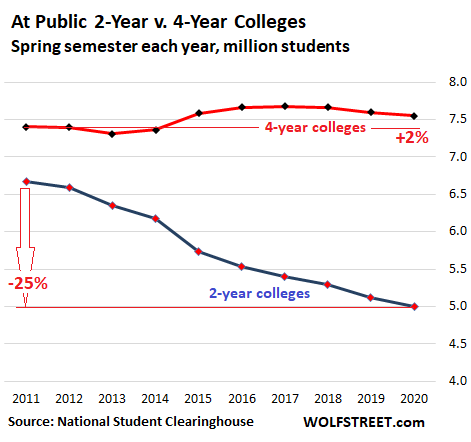
Enrollment in public schools has diverged.
At public two-year schools, the 2.3% drop in enrollment this year added to the drop in prior years; and since the spring semester of 2011, enrollment has plunged by 25%, or by 1.67 million students, pushing the total down to 4.997 million students (blue line in the chart below).
At public four-year schools, enrollment had seen increases in 2015 through 2017 (7.68 million students), as some of the students that were abandoning for-profit colleges decided to continue with their education at public schools. But then enrollment began to decline again, dropping 1.7% since 2017, to 7.55 million students. It remains 2% higher than it had been in 2011 (red line in the chart below):
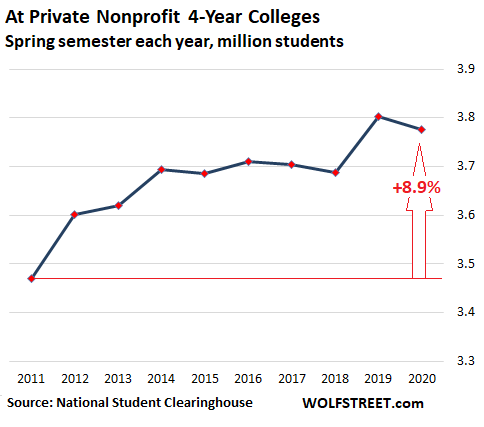
Enrollment in private non-profit colleges falls, after surge last year.
Back in the spring of 2019, enrollment at private nonprofit four-year colleges – this includes some of the most elite universities in the US – had jumped 3%, the largest percentage increase since 2012, after years of stagnating or declining. But this spring, enrollment declined 0.7% to 3.78 million students. Nevertheless, since 2011, these institutions have gained 8.9% in enrollment:
Majors.
Of all students with declared majors (9.06 million), the top two majors combined – “Business, Management, Marketing, and Related Support” and “Health Professions and Related Clinical Sciences” – accounted for 28.5%. Over the two years since 2018, however, those majors declined by 3.0% and 2.1% respectively.
The third largest major – “Liberal Arts and Sciences, General Studies and Humanities” – dropped by nearly 12% in those two years.
Enrollment in “Computer and Information Sciences and Support Services,” the sixth largest major, jumped by 10.4%.
The table below shows the broad categories of majors, how many students declared them their major in the spring semester 2020, and the percentage change from two years ago.
The STEM majors (science, technology, engineering, mathematics) are spread over a number of majors in the list below (here’s UC’s 32-page list and descriptions of STEM fields, ranging from “Agricultural Animal Breeding” and “Aeronautical/Aerospace Engineering” to “Petroleum Technology” and “Systems Engineering”). If your smartphone clips the third column, hold the device in landscape position.
| Major | Spring 2020 Enrollment | % v. 2018 |
| Business, Management, Marketing, and Related Support | 1,527,889 | -3.0% |
| Health Professions and Related Clinical Sciences | 1,052,148 | -2.1% |
| Liberal Arts and Sciences, General Studies and Humanities | 932,596 | -11.9% |
| Biological and Biomedical Sciences | 575,084 | -0.7% |
| Engineering | 550,966 | -3.0% |
| Computer and Information Sciences and Support Services | 467,204 | 10.4% |
| Psychology | 457,506 | 5.5% |
| Education | 438,195 | -2.6% |
| Social Sciences | 422,438 | -3.4% |
| Visual and Performing Arts | 387,897 | 1.5% |
| Communication, Journalism, and Related Programs | 309,306 | -4.4% |
| Security and Protective Services | 272,986 | -1.8% |
| Multi/Interdisciplinary Studies | 228,253 | -0.4% |
| Parks, Recreation, Leisure and Fitness Studies | 221,086 | -3.4% |
| Public Administration and Social Service Professions | 132,563 | -4.7% |
| Physical Sciences | 128,317 | -9.1% |
| English Language and Literature/Letters | 126,902 | -9.6% |
| Engineering Technologies/Technicians | 98,402 | -4.0% |
| Family and Consumer Sciences/Human Sciences | 88,081 | -8.7% |
| Mathematics and Statistics | 87,493 | -2.4% |
| Agriculture, Agriculture Operations, and Related Sciences | 84,886 | -3.1% |
| History | 81,024 | -4.1% |
| Natural Resources and Conservation | 80,801 | 3.0% |
| Foreign Languages, Literatures, and Linguistics | 53,644 | -7.7% |
| Architecture and Related Services | 42,624 | 7.4% |
| Philosophy and Religious Studies | 31,713 | -8.1% |
| Transportation and Materials Moving | 30,887 | 12.1% |
| Theology and Religious Vocations | 25,494 | -11.3% |
| Area, Ethnic, Cultural, and Gender Studies | 25,735 | -1.1% |
| Legal Professions and Studies | 23,166 | -2.6% |
| Communications Technologies/Technicians and Support Services | 20,440 | 8.5% |
| Personal and Culinary Services | 14,066 | -19.7% |
| Mechanic and Repair Technologies/Technicians | 13,967 | -9.3% |
| Construction Trades | 10,170 | -1.5% |
| Science Technologies/Technicians | 7,886 | 0.9% |
| Precision Production | 5,678 | 0.1% |
Undergraduate v. Graduate Students and Age.
Of the total student enrollment in the spring semester, 15.6% were graduate students. Their number, 2.73 million, was roughly stable with a year ago, after two years of increases.
The age of all students as a percent of total enrollment:
- Under 18: 4.1%
- Between 18 and 24: 60.2%
- Over 24 years old: 35.6%
Average age of undergraduate students:
- Full-time: 22.7 years
- Part-time: 27.7 years.
Average age of graduate students:
- Full-time: 30.5 years
- Part-time: 35.4 years.
Men are leaving the classroom.
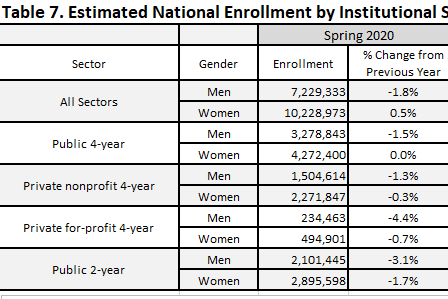
Men accounted for just 41.4%, or 7.2 million students, of total student headcount in the spring semester. The enrollment of men has continued to decline every year since 2011, including by 1.8% this spring semester, by 2.8% a year ago, and by 1.9% two years ago.
Women accounted for 58.6%, or 10.2 million students, of the student headcount in the spring semester. This spring, enrollment ticked up 0.5% after having declined by 0.8% in each of the prior two years.
Now what?
Even before the pandemic and the lockdowns, these were very tough dynamics for this huge sector of higher education that drives so much and engendered entire industries, such as text-book publishers, and asset classes such as “student housing” and student-housing CMBS, whose delinquency rates began spiking last year.
While a few colleges have been able to grow their enrollments in recent years, others have experienced declining enrollment. The huge expense of higher education in the US surely acts as a ceiling for many potential students. And a hot job market, as it was before Covid, gave many potential students appealing alternatives.
Now all this is history. Enrollment going forward is in turmoil. There are voices now recommending that students consider taking a year off and go do something else, until the dust settles. Some schools are switching at least temporarily some or all of their coursework to online, and students can live anywhere to take those courses. There are other big changes now underway.
And many local economies centered around universities will experience considerable upheaval, including in their real estate market and its creditors and investors, as these students suddenly don’t show up, or don’t show up in the usual numbers – that in many places have already been declining for years.
There is a meme going around among student-loan borrowers: Only morons still make payments on their student loans because these loans soon be forgiven anyway. More and more borrowers are using the options available to defer the loans. This produces the phenomenon of stalling loan repayments that is causing student loan balances, despite the declines in enrollment, to surge. Read... The State of the American Debt Slaves, Q1 2020: How Are Consumers Positioned Going into the Crisis?
Enjoy reading WOLF STREET and want to support it? You can donate. I appreciate it immensely. Click on the mug to find out how:
![]()


The whole students industry also faces another head-wind.
While the premise of studying for a degree implies a desire or attempt to move into up into middle classes and progress from there, the current worldwide corrupt financialisation construct guarantees that very middle classes demise and therefore lesser necessity for degree educated anybody in due course.
And very soon indeed.
Or you could argue that increased financial/legal education arms students with defensive tools against “corrupt financialization”
I won’t argue the fact that the dark side is winning…but like all tools, financial/legal education can be put to both good and bad use.
“corrupt financialization” = A contract an adult (who is allowed to vote) voluntarily agreed to and signed on the dotted line.
You don’t need “financial/legal education arms” to fight this. Don’t play the game.
Now – that choice is a whole lot of hard work and hard decisions. Instead of just signing a piece of paper and being showered with money for four year – the young adult may actually have to:
Work while attending/Coop
Go to a college that was not their first or second pick
Go to a community college for two years
Join the military/Reserves
Go to the most affordable state college they can find
Etc.
How about the debt you inherit as a newly born from your previous generations? You didn’t sign for anything, but in later life you still have to work and pay taxes for it.
OT: I think physically going to a college (campus) is not the way to go in the future. The C19 situation has shown us that we can have and do a lot of things right from our homes. Studying is one of them. The only reason to pysically go somewhere is to socialise and build a network. The latter being questionable in some circles, because in my view it also encourages cronyism.
I agree. There are too many majors that will not have any adequate return on investment given the financial collapse that is coming: to many employers will go bust, so there will be fewer chances for majors like liberal arts.
The ultra rich have propped up the stock markets with the help of the bankster’ allegedly Federal reserve. They have trillions invested but may stop that once they get what they want in fall. Then, with any more waves, we will also enjoy another 1929 crash.
Other than software related fields, return on investment isn’t very good for college degrees in general, even STEM.
Few engineering jobs have been created during the past 20 years. I was a EE from the late 70s until the late 90s. Then I changed careers into software because the electronics industry was offshored. As such, I compete with 20 somethings and H1Bs.
Young men would do well to consider the trades.
A few years ago I was at a talk by the president of a mid tier public university in Oregon ( Western Oregon U). He explained the financial dynamics of his institution. The bottom line is that state support and in-state tuition did not bring them to break even. They were only able to keep their head above water because of the foreign students paying high tuition. One thing is certain this fall. Out-of-country students will be showing up in much smaller numbers for multiple reasons. I think this will have grave consequences for all but the most well endowed schools.
You should have asked him.
“What percentage of the college’s employees do not teach a single class?”
It will be astronomical. Tell him to start there.
“How insane are you pensions?”
It will be astronomical. Tell him to next go there.
“How many feel good degrees do you offer that make no sense in the marketplace?”
Etc.
“the bottom line is that state support and in-state tuition did not bring them to break even.”
Looking at how much in state college admissions have fallen, they could possibly partly offset each other. More likely, many states will have to close some schools down and then increase some class sizes in remaining schools. A big question for each state is that if attendance is falling, how will funding, especially funding per in-state student be effected?
Overall though, I do question how useful business degrees “non-MBA” really are, it does seem like for non-science degrees; the number of students for each degree program should be capped.
For most of the majors at college, I do question if they really needs to be a college major for it. Instead, the government could simply have a wealth of free downloadable text books, videos, and more; similar to the free not for credit online classes out there. In the past when the public was willing to make college cheap, it made sense to have most of these majors like history, but if, the public is no longer willing to do it; it should be brought to an end. Instead, for many things like history, you could simply do exams and be certified to have obtained knowledge in that subject.
Student loans might need to be outlawed, if America needs healthcare workers, the public better be willing to pay for little Jimmy to go to college.
Accountants are dead useful.
Yes,
But, do accountants really need a college diploma or can they self study and take exams and be certified. We would assume that 18 year olds would get starter office jobs and could as they progress over the years, get certifications to expand their available job opportunities.
For accountants specifically, we could also have a really good easy to use accounting program or just tone down our intentionally complicated so as to have loophope laws; that would make accounting easier, but, either way, the above way, would still work.
TR: Do you think you can run a corporation like ENRON taking an accounting course from the back of a matchbook cover?
Ambrose Bierce,
I never really considered companies like poor Enron :(
To be clear though, the textbooks and all the information they would self study would be equivalent to current college classes. Self study certifications wouldn’t be available for engineering or hard sciences like biology those would still require university, but, if we cut all the side stuff like history, it may take less years to graduate.
Here we have another example of people who think the study of history is memorization of important names and dates, just a mass of knowledge to cram into the head and regurgitate on a multiple choice exam. Sad to think that was probably most people’s experience of a college history class. But for anyone who’s ever been in a quality history program, sometimes conducted as intimate round table seminars, with a world-class scholars, like I have (at Cal while working 4 nights a week at restaurants to pay my way, no loans) well, that person knows something about the study of history that most others can’t even imagine.
Grammar errors notwithstanding! LOL. At Cal they didn’t warn me about rushed-responses on social media.
Stephen C.,
The problem is very simply that America isn’t really funding universities like it needs to. And the current system is failing, as demonstrated by falling admissions and skyrocketing student loan debt. Some less essential things will need to be cut. For things like history, how many historians do we really need? Even without college degrees in it, there would always be enough people to show interest in it, to keep the field going. Philosophy and many other degrees are the same way. They are many other ways, such social sciences could survive and thrive without being in universities.
If you have a better solution, we are all ears.
Also attacking grammar is one of the weakest forms of argument. It’s akin to an instant fail.
When I was 25 my parents realized I was going nowhere fast as far as jobs/career went, and offered to put me back in school (it was my best/only option, unless I wanted to be a professional bartender, but there are health risks). My dad was a career counselor at the local JC where I reentered academia; he prepared my class schedule and told me:
“You’re going to major in business because it can’t hurt you.”
re: ‘Overall though, I do question how useful business degrees “non-MBA” really are’
Got my (mediocre student) son into Officer Candidate School and an ensign’s commission in the US Navy.
Right now, one of the main reasons alot of young people do to college. Is that when it comes to getting hired, from the time they graduate to the rest of their life, every time they go to apply for a job it will always be college graduate vs not. Many young people think that in the future without a degree they are screwed.
If America, was willing to properly fund college it would be a whole different situation. There are ways to bring down the cost of college like more school weeks in a year and graduating then in 3 years. But if, America is totally unwilling to bring the money the college graduate vs not situation can only be solved 1 way; greatly reducing number of college students.
Alot of people on this website, don’t seem to understand just how expensive college is now, especially after the cost of living has gone up so much. They are alot students working those 4 nights a week just to cover their car, books, and other essentials without even being able to pay anything toward tuition, dorms, or the mandatory meal plans.
This isn’t to say your business degree or history degree don’t have value, this is to say, young people cannot afford to go to college. If they don’t manage to get a job that pays well afterwards, they are in for potentially a couple decades of being extra poor. The nuclear solution is to reduce college to only the essentials like engineering, hard sciences like biology, and things like healthcare. These things require proof of competency or lives are lost. Everything else can be done in much cheaper ways. I would prefer that college be an almost free 3 years for most thing, but, that doesn’t seem likely. The question of the value for a business degree is whether going to a current college is worth $80,000 compared to self studying the exact same materials with pre-recorded lectures.
And you have to remember that financial situation gets worse for those 18 year old’s heading off to college every year.
According to the table there is declining demand for work in the Physical Sciences and Engineering. So much for the ‘shortage of scientists’ mantra I’ve heard screamed at me over the years.
People avoid sectors where there are no jobs.
Or at any rate no jobs for American citizens.
The main problem is that as America got more automated, the number of hours worked by an average worker should have gone down. Effectively, sharing the better paying more useful jobs among more people. The opposite was done.
Those jobs would still provide a middle class lifestyle, but, some things like eating out, would be more expensive. As it requires alot of labor over time, for something you can normally do yourself.
Not all of us do.
I went to university to study what interested me, physics, not to train for employment. Thirty-five years later and I have not needed or used my degree for anything, but I have no regrets.
My advice to my friends’ kids who are about to start college is, “Do your best and study what you want. Things will work out.”
One of these kids is set to attend DePaul; attend being the question mark these days.
Thinking back though, the cost of going to the U of MN forty years ago was not anywhere near the cost it is today. Going to school just to learn versus going to train for a job would be more difficult now I reckon.
Yeah – because if you wanted to “just learn something” I can’t think of a way you could do that today, for free, anytime day/night, like online or something…
I reckon.
Please let me clarify what I meant by “more difficult.” This was about the decision and cost – not by being able to study online.
You make a good point about today’s technology. For the garage mechanic, YouTube has great how-to videos for example.
Some of what I learned in college was intuitive already, and could have been done online these days. But much of what happened in the classroom was from good professors teaching and questions from fellow students that they answered (fellow being the operative word as not too many women studied physics. I would hope that has changed).
Maybe it was ego, but once I started, I was not going to quit. Getting my diploma was important, not for doors it would open, but for the satisfaction of accomplishing a goal I’d set for myself.
rhodium sums it up well, “The thing is most people don’t think of college as education for education’s sake.” I will remember that line when see my friends’ kids.
Part of college is teaching you HOW to think.
For example, with a background in physics, you were trained to
Describe the problem
Bound the problem
Look for ways to simplify or zero out variables
Look for ways to apply known solutions
Approximate where necessary
Be very careful with units and conversions
Verification of the solution
Etc.
Skills you probably use everyday of your life.
“Thirty-five years later and I have not needed or used my degree for anything,”
That’s true. And these skills, although not related to physics, were used in my family wheat seed genetics company.
I do encourage kids to just study what they are into. Maybe that’s why …
Totally agree. I went for computer science, which is in many ways a degree in logic. And most of what 2banana lists above would apply.
The question I have, is would my reasoning and logic skills be as appalling as those of my friends and associates, if I hadn’t gotten the degree?
I can’t imagine they would be, because I think I was drawn to computer science because I was good at logic and reason.
Does one need a degree in logic to understand the irrationality of ones own biases and contrary behaviors?
Are you honestly searching for the truth?
That said, going to school definitely has huge benefits with respect discipline and structure and focus and community and socialization, etc etc
But in no way Does it need to be as expensive as it is today.
Computing power And online courseware have become nearly limitless and close to free,
Yet the cost of An education at a University has gone through the roof. It’s absurd.
At my job there have been a number of interview candidates who were regarded as highly suspicious mostly because even though they had relevant experience, their college degree was considered unrelated to the field. For some reason some of my co-workers seemed distressed about it, as if these people were failures for not working “in their field” (one was a history major…). I didn’t think that was a big deal because that’s kind of my case, although I got the same squinting suspicion when I interviewed (but at least I assured them apparently, bc I got it).
The thing is most people don’t think of college as education for education’s sake. They think it’s supposed to be vocational so if you don’t fit their limited view of what’s supposed to be what you might very well be pointlessly punished for it.
re: “Thirty-five years later and I have not needed or used my degree for anything,”
A little over thirty-five years ago I got a BS in Computer Science, and a great job in the nascent ‘tech industry.’ I’d say I retired a couple years ago, but I’m still doing tech support for friends and family.
Once, I was told that ‘aerospace’ was a great money-making opportunity. Within two years, former Boeing employees were selling pencils to feed themselves.
The purpose of education is not to make money. The purpose is education, itself. That would be the ‘drawing out’ of the individual into a more ductile and enhanced human experience. A good scientist isn’t ‘hired’. Instead, a good scientist follows a profession. A company is lucky to find a good engineer who will agree to work for them.
If there ever was a shortage of scientists or engineers, it is because our society devalues logic (either inductive of deductive). Instead, it values (and rewards, culturally) flim-flam, appearance and dishonesty (the ability to steal the resources of another person without producing anything of real value, something providing heat, shelter or food). Thus, we encourage the later ‘skills’ of flim-flam and demean the former involving logic.
Now that we’re #1 (the epicenter of global Covid19 infection), we see the long-term cost of flimflam. The quarterly report doesn’t reflect long-term stability, and the benefits of an investment in rationality (a position upon which our country was at least partially founded) cannot be measured quarter by quarter.
‘Short-sighted’ has a negative connotation for good reason. We are a ‘short-sighted’ society.
Daedalus:
“Once, I was told that ‘aerospace’ was a great money-making opportunity. Within two years, former Boeing employees were selling pencils to feed themselves.”
Silly commentary Daedalus…you can do better than that!
I think ur missing his point:
Investment in logical thinking is Ultimately better than An investment in sophistry.
But we have more lawyers per capita than anyone else, that has to count for something in a rule based society. Where Would we be if there is no one to tells us how to interpret the rules.
If only lawyers would actually help interpret the rules and translate it into good practical advice. But it seems lawyers (particularly “high profile” lawyers) are busy on pointing out loopholes and showing their clients how to defeat the purpose and intent of the rules without being able to get punished for doing exactly the things the rules were supposed to stop and prevent as they cause long term harm to society.
The practice of US law has become a library science or an exercise in writing fantasy. The exercise of logic is now incidental.
There is always a dearth of physical scientists and engineers that will work cheaply enough. Has been in the past, will be in the future. We don’t have the result we would like because the supply to meet demand is now global. Mathematics is not a spoken language.
At my last job on the (U.S.) East Coast, our company (a major fortune 500) had a specific policy to not hire Americans.
We were required to go to our India based ‘Center of Excellence’, find staff there, and if we could not find anyone there that could be H1B’d in, then we were allowed to look for an American for the role (which of course would cost more..but that was not the reason at all ;-) ).
No wonder no one wants to study STEM and engineering anymore..
Which is in direct violation of the H1B law.
H1Bs are only allowed to come to America and to be hired when a company in America can’t find an American to fill that job.
How did we get here in opposite land? Why is this allowed to continue?
Because “big tech” wants it. And they have the influence and power.
The spirit of H1B visa is very noble: To find foreign workers which can’t be filled by local talents. But if not all then most of the H1B visas are used to displace US workers by compliant workers from foreign countries esp India. Why India: Because an Indian on H1B would take atleast 10-15 years or more to get his greencard as the wait period is long and unpredictable. This wait period makes Indians on H1Bs an excellent worker which can happily work even on weekends.
I am an Indian, and was on H1B
No kidding, the worst are the rule breakers who leverage H1B to essentially import workers and entice them with hope and then toss them back after the term is up.
The consultancies are usually the worst of the lot.
Sorry, but H1-B was never noble. It was a scam from day one, based on the completely false premise of a supposedly dire STEM shortage. Which has been repeatedly refuted by unbiased studies. So no wonder it was riddled with fraud and abuse from the beginning.
There is an O visa for truly extraordinary talent that is rarely used because it is actually hard to get. H1-B (and several other guest worker visas) have so many loopholes and so little enforcement that obtaining them is incredibly easy.
Bingo! And this has been going on for at least a couple of decades.
If anything, this will be the popping.
There has been so much “student”housing built UP in the past 5 years it’s truly incredible.
So what do you call the 10.4% increase in enrollment for Computer and Information Sciences and Support Services?
Most are foreigners, especially in the graduate programs. They usually get work study which gives them free tuition on top of getting the spot.
Yeah, but afterwards a lot of them will go to top companies and they are not cheap.
Also number of available TA spots are limited. Max of 20% of grad students will be on work study. The rest took out loans.
Google, Facebook, etc pretty much vacuums every single PhD in Machine Learning out there. Likewise people with Masters/PhD in Distributed Systems.
Those guys start at 200K straight out of school, so not cheap.
1) Computer and Info jumped 10.4%. China flooded top computer department, for decades.
2) DOD and robotic next to Chinese students in CMU.
3) Off campus apartment, near student party, for alumni, will have
problems.
4) College amphitheaters might stay empty.
5) Many Chinese and other foreign student cannot find employment, because they are riding on the back of their employers, seeking citizenship. Only their very best, with advance degrees, will find employment.
6) Female students, US citizens, are replacing Chinese students, studying cyber.
7) To survive, colleges will cut capex, change their business model.
8) Part time professors, moving from school to school, will be
tossed out from academia.
Lotsa top-heaviness in colleges and universities, with administrators growing like barnacles, as the hull rotted underneath, in recent decades… but of course, it will be the adjuncts (and food service, and janitorial workers) who face the sharpest austerity.
Rural college towns that weathered the hollowing-out of the countryside better than their industrial counterparts are in for a rough ride. As Wolf’s article shows, enrollment was already declining significantly, but corona virus has turned a chronic problem into an acute existential crisis for many schools.
Male/Female percentage of the population is 49.4/50.6. (2020)
There are no “male only quotas” and there are no “male only scholarships” and there are no “special outreach programs for males” for going to college.
And the results are in. Funny how there is no outcry over the disproportionate numbers.
Maybe, in the end, it is a good thing. College degrees, with a few exceptions, are not worth the cost and debt anymore.
“Men accounted for just 41.4%, or 7.2 million students, of total student headcount in the spring semester. The enrollment of men has continued to decline every year since 2011, including by 1.8% this spring semester, by 2.8% a year ago, and by 1.9% two years ago.”
Without even looking, there is no way male/female population spread is 1.2%. Can’t be.
It absolutely can: just look at the over-80s where women vastly outnumber men due to life-expectancy differences.
I also think Wolf’s 40% number is suspect, or at least isn’t reflective of the generic 18-22 undergraduate school population.
For instance, it wouldn’t surprise me if more women went back to school to get an edge in the job market after taking time off to get a family started.
There could also be racial demographic differences depending on cultural values of different populations.
Wisdom Seeker,
For example:
43.3% of the students in four-year public colleges are men.
39.8% of the students in four-year private colleges (including our elite schools) are men … and 60.2% are women… there is a message here, no?
Look for yourself:
The other side of the coin is that men in college must be in girl-nirvana, with that kind of ratio of men to women. When I went to college, women were a minority, and you had to out-guy the other guys to get the girl’s attention.
The cliche is they go to college to get a family started. They used to call it an MRS degree. I don’t think it is being sexist to want to send your offspring to the best (Ivy League?) college they (you) can possibly afford. Men or women, the people you network with in college is what you learn. When they remind us that Bush and Kerry for instance, were C students at Yale, you wonder, what happened to the A students?
Wolf, I have kids in college and the demographic numbers put out by the typical school do not jibe with your data. And there are still engineering schools that are male-heavy.
There has to be something special going on. Is it that men are being excluded, or are they choosing other options?
High School Graduation Rates: 2% lower for males. And the underlying population has slightly more females due to birth demographics. So if men and women chose college equally, one would expect a 48-52 or 49-51 gender balance based on the source demographics coming out of high school. Look also at
military service ~ 80-85% male, 15-20% female. That will tilt it a bit further.
Looking at a somewhat random, somewhat Cali-centric set of specific top-tier schools:
UC Berkeley Undergrad – 47.4% male, 52.6% female.
Harvard Undergrad: 50.5% male, 49.5% female.
USC: 48.9% / 51.2%
U Michigan Undergrad: 50.3/49.7%.
…
Of the first dozen schools I looked at, the only ones with a gender imbalance >5% excess female were NYU and UCLA (42.2/57.9). But other schools like Purdue (U of Indiana, 57.6/42.4) and CalTech are majority-male.
I think one needs to look carefully at *where* the extra females are going to college, and what they are studying, because they aren’t obviously outnumbering men at the premier public or private universities. It may depend on which programs are popular at each school. Could it be that there are enough women-only schools left (vs. fewer men-only)?
The other question is the age of the extra female undergrads.
Finally, the literature I’ve read says that schools with a high proportion of females have more of a hookup culture, and those that are more balanced have more traditional dating. Depending on your perspective a “girl-nirvana” might not be a good thing for everyone’s long-term social development.
The U of MN is a large school. The 1985 graduations included 15 with physics degrees. 14 men and 1 woman. My quantum physics professor and kids lived in my neighborhood and we went to junior high and high school together.
The son was two years older and got his bachelors, masters & PhD in five years. I got my bachelors in five. The daughter was two years behind me and was the only female in my class that graduated with us.
It probably goes without saying that they had ‘smart genes’ in their family.
In establishing the Rhodes Scholarship in 1902, Cecil John Rhodes restricted applicants to males only.
But some time ago – perhaps in the 1980s – the members of the Rhodes Trust violated the old bugger’s wishes and opened applications to females.
32 full scholarships are awarded to citizens of the USA every year – of which 21 were female in 2018.
I wonder what Darwin would make of all this?
The restriction made sense in 1902.
Harvard didn’t allow female undergraduate students until 1920. Yale not until 1969.
Foreign Student Enrollment
USA -10%
Canada +30%
America’s braindrain is Canada’s gain.
I was wondering when someone was going to point this fact out. Of course xenophobic Americans are probably celebrating but they are too stupid to realize that educated immigrants create millions of jobs. Their goal is to make the whole country look like Mississippi. Meanwhile Canada is winning! Make Canada Great Again should have been his slogan.
There is so much wrong with your statement I don’t know where to begin. When ten percent of your population doesn’t even belong here, asking them to go home so that your average Mississippian (many who are poor black people, btw) has a fair wage does not make them “xenophobic.” Also, Americans have always welcomed immigrants, but this fact seems to elude you.
Canada also has a law that does not allow guest workers until it has been proven that there is no Canadian that can do the work. I guess that makes Canadians xenophobic. Quelle surprise.
Re Canada immigration, etc:
Canada does not allow guest workers unless there is a proven shortage that is not manipulated by employers to save on training costs. For example, in aviation it was common past practice to hire from overseas high time pilots to immediately qualify for insurance coverage and for companies to avoid training up their employees. This has been stopped, and so has bringing in any other employees if a Canadian can do the work on a level playing field.
What a concept, a country looking after its citizens.
As for immigration, an applicant is admitted on a point system to address anticipated or current needs as discovered by survey and census. If you have a trade, a medical degree, or a specific skill set deemed necessary for our future needs you will be granted entry as a landed immigrant. This excludes most university degrees. My sister referenced the possibility of her US children moving north last year. I didn’t have the heart to tell her none of them would qualify including her engineer son, accountant son, or teacher daughter.
University should not simply be an extension of high school and adolescence. Nor, is attendance necessary for education. An example of this is my father-in-law. FIL emigrated to Canada from Manchester in 1955. He was a journeyman printer. He also had a grade 8 education as a result of living through WW2 bombing and dislocation. He died just 5 weeks ago, but along the way taught himself to read Egyptian hieroglyphs, speak basic Japanese, became an accomplished painter, sculptor, built a boat and sailed to the south seas for 3 years after learning traditional navigation in 1960 (my wife spent 3 pre school years on that boat). He could play the shakuhachi, and started to learn piano at age 70. He was also a damn fine drummer. At age 89 he was still troubleshooting his Apple computer and traded in his sketch books for an I Pad about 5 years ago. He was an accomplished fly fisherman and tied his own flies.
Grade 8. Our house is filled with his art work.
Universities exist as a gate keeper; granting professional certifications and pricing out the riff raff…….like my FIL.
As I used to tell my school superintendent buddy when he touted post secondary as the only way imaginable, “My son works fewer days than you and earns 2.5X your salary working as an industrial electrician. Plus, there are no politics with his job”. Furthermore, son had no student loans by going through an apprentice program. Earn while you learn.
As if the ruling class in Mississippi treated its Black population well in the years before immigration law changed in 1964, and as if they’d do so when/if your fantasy of purging “illegals” comes true.
Not a lot of honor in reading about college students accepting & agreeing to repay student loans (now totaling over $1.6T), while at the same time planning to never actually pay them back.
A little more than 1/3 of the age cohort goes to college and accepts student loans.
It’s disappointing to read of grossly entitled students with basically dishonest motives, expecting the remainder of society to fund their 4+ years of fun living, football games and spring breaks.
That is a very broad brush that has no basis in reality.
From The US Department of Education Web Site (latest numbers I can find):
“Today the U.S. Department of Education announced that the fiscal year 2016 national federal student loan cohort default rate (CDR) decreased from 10.8% for FY 2015 to 10.1% for FY 2016, a 6.5% decline from the FY 2015 rate.”
Additionally the median Student loan in $17,500. Not even a car loan. Hmmm…seems fairly responsible.
Plus all the students who went to less expensive colleges, 2+2 programs with community colleges, joined the military or actually paid for their college with savings/work (yes, this still happens at very affordable state schools).
2banana
“…That is a very broad brush that has no basis in reality….”
Not sure what you statement refers to, or what your point is.
Bank regulators generally shut down a bank when loan default rates approach/exceed 8%; even you admit student loans default at over 10%.
I understand the difference between median & average, but all I could find was average student loan debt, which ranges from $29,000 to $35,398 (different articles quote different numbers for 2018; go figure). I realize median would be a lower number.
I contend college undergraduates are too immature to make unassisted (guidance from mom & dad) major credit decisions; they’re further handicapped by having no realistic idea what their post-graduation income will be. The hellacious mess of the $1.6 Trillion student loan program simply proves my point.
link: https://www.investopedia.com/student-loan-debt-2019-statistics-and-outlook-4772007
Javert Chip,
“…but all I could find was average student loan debt…”
This is from a 14 page report by Moody’s that I have cited many times:
“Also reflecting the varied student experiences, borrowing is highly concentrated among a small percentage of borrowers with large loans. As of year-end 2017, the average amount borrowed by the almost 45 million federal student loan borrowers was $34,000 while the median was around $17,000-$18,000.”
However, I cannot link the report because it is not public. Moody’s emailed me the PDF, and I don’t think they want me to post it online. If you’re interested in the report, let me know, and I’ll email it to you.
To paraphrase an old saw – When a student owes a lender $17,000 (or less) it’s the students problem, when a student owes a lender $150,000-200,00 it’s the lenders problem.
Meh let them enjoy a couple good years in their prime. Personally I dont mind paying toward it.
These kids are lied to by the student loan program which promises to forgive loans if they work in public service. Almost nobody who works in public service gets loan forgiveness after the promised 10 tens.
I hoped that Petunia’s comments couldn’t possibly be true.
However, even a cursory Google search turns up extensive commentary supporting what she said.
I’m not wildly enthusiastic about the concept of student loan forgiveness (students are knowingly purchasing a dubious product), but if the government made the promise, then that commitment must be met.
It’s incomprehensible that tens of thousands of ex-students appear to have been manipulated into working for 10-years only then to discover 99% don’t qualify for loan forgiveness.
A quick Google search can’t differentiate between student naiveté and a deliberately duplicitous political process, but, at the very least, government bears the responsibility of explaining the rules.
They could join the army. Seriously, a buddy of mine did that after his undergrad. It was one way to get the debt paid for legitimately.
I think if anyone even entertained the thought today, they’d be lynched on the spot.
In other words – get the promise in writing, in advance, all the rules, and read them thoroughly. A good policy for the rest of your life.
Or, you can just click “I agree” on the EULA and let them do whatever they want.
Haven’t dishonest motives become the American Way? It is in the Halls of Congress and at the FED. Where else can an entity loan digitized fiat and get paid? And spread the debt system to engulf young strugglers hoping to make it.
And the bulk of college enrollment is to study business. I suppose the successful ones will becomes Private Equity Raiders. Others just common Corporatists. Isn’t maximizing gain and minimizing pain expense something one expects to learn in business school?
The dishonor is in having a system that leads young citizens to compromise themselves for the priveledge of getting employment, much of which rests on getting a degree or credentials – however dubious the real value thereof.
How about the kids who obtain an expensive degree….then intern. Lets just call it free suck hole work for resume fluff and connections. 1-300K for a degree paid by family and then they work for free to get a foot in some door.
Something is very rotten with this concept. No wonder there is so much corruption. Everyone is trained up in a racket. Tony Soprano would be proud.
Students and families making multi-hundred thousand dollar decisions to “buy” a college education are responsible for these decisions.
We have devolved a new meaning for the words “diploma mill.”
No one thinks of college as a business but behind the scenes of a peaceful, tree lined campus that is the way it has to be run. You have to supply a useful product to your consumer or you consumer stops buying the product. At today’s incredible prices small non profit liberal arts colleges should be closing en mass.
Yet if I asked you how many non profits closed in the last four years, 2016-2019 what number would you guess have closed their doors. The number is 20 which proves that zombie schools like zombie corporations can live forever in a debt fueled economy.
You misconstrue a college education as a product. Currently a college education is similar to a business license. You want to do business, you have to purchase a license from the governing authority.
International students are 21% of Harvard’s student body. Chinese students are the largest foreign student group making up 4% of the student body. Canada and India are #2 and #3.
The American economy
2020………what keeps the US dollar floating in mid air is good for the USA and a modern miracle.
Our economy consists of Government, Arms manufacturing, Food production, Illegal Drugs, Medical Services, Financial Services, Education,Technological Design and a few odds and ends.
Almost all of it not subject to supply and demand…….its almost all produced at whatever we decide to spend on it and they (includes we) must pay the price.
Efficiency is not part of our terminology. If 5 teachers could do……lets hire 15 and pay them 20% more. Administrators who used to wear sweaters and vacation at the local lake now wear silk and go to the south of France. Education is just a symptom of a bloated inefficient noncompetitive economy in which no one feels pain……except the poor slobs working in sweat shops overseas making all the crap we dispose of.
But, but, but,,, what we spend on Internet Advertising is bid up by demand.
1) Rotation and change of character.
2) There are > 1M students in engineering dept, computer science schools… That number will slightly fall during the next recession.
3) At the top of the list there are : 1,528K students in business, mgt
and marketing. Number #1 will have a major haircut.
4) Number #3 : liberal art 933K students can easily lose 200K-300K
students.
5) At the bottom, rotation in favor of private two years tech schools, for 25K to 30K from start to finish. Their number might double or triple in a short time.
6) Brainless Canada is being taken over by foreigners.
Brainless Canada? The average IQ is higher in Canada than the US. The US and Americans in general are now international pariahs hated the world over and held in contempt. Nice job.
So you want to be somebody’s hero? Think about this…
Better a pariah than to sell your soul for someone else’s affirmation. But you’re such kind people….
What do they make in Canada that requires said average IQ?
Looks like the nursing home thing in Ontario is pretty bad.
Yellow snow?
In this case the average is brought down by the vast number of sub-100 IQs. Eh? You are a hoser.
Oh but our government is politically correct in their own mind.
We are actually being held hostage to their own policies imposed on us.
Michael,
And which country voted in Clorox?
Time to stop making idiotic lists.
Granddaughter graduated last year from a 4 year Texas state college. For years I suggested she go into nursing as there are jobs, and will be for a good while. No, she wanted to get a degree in Health Services, whatever that is.
During graduation exercises, I listened to over 200 students “walk” and get their degrees. I would guess that the titles of these degrees were not created when I went to college in the 1970’s. I had never heard of the vast majority of these degree titles nor would I have ever imagined where the person receiving the strange to me degree would find work.
It took granddaughter a while to find work, and it pays about $14/hr. She works in a “non profit” health related company as a phone solicitor trying to get contributions. This is Houston, where many thousands of health care workers exist. Maybe she can get a better job soon….something like a receptionist in a doctor’s office. The colleges are pumping out vast numbers graduates with no marketable skills.
Colleges should offer a degree in cutting your own hair. Seriously they’ll have a ton of applicants.
Two Words…
Flow-Bee!
Already exist.
Well, perhaps as apart of a beauty studies degree.
1) The top 15 majors have about 8M students.
2) During the 2008/09 recession there were x2 options :
3) send the young generation to college class rooms, either to study or have a party, – at their own expenses, – for as long as possible.
4) Send them to the unemployment lines and to the streets, to protest and riot, like in the 70’s.
5) If student debt extrapolate, that’s the next president headache.
Michael, this is not a problem. We will simply sell some Treasuries and use the proceeds to retire student debt. The next in line can worry about paying off the Treasuries – a bit later.
Average age of full time grad students = 30.5. Why so old?
The greatest increase in both #s and costs have been in administrative . Look for major cutting in this area in the next few years.
This is a case where a few outliers will skew the average. I’d really like to see the median instead here.
It would only take a handful of 60-somethings among dozens of 20-somethings to push the average up to 30.
You won’t find many grad students under age 22. But you can find a lot of grad students in their 40s or later, including some retirees who go back to school just to get a new education.
Rcohn,
I agree with Wisdom Seeker that it would be nice to know the median as well. Nevertheless…
When I got my MBA, it was almost required that you had work experience after college to be even admitted to MBA school (UT Austin). Almost no one went to MBA school right after college. I was 30 when I graduated with my MBA. And I fit right in.
Also, many graduate programs take forever, including med school. PhD’s in general take forever. Many programs require years of field work or lab work.
Welcome to the wondrous world of “post-doc” temporary employment.
Learn a trade. Honest work, huge demand in most categories. Make more in a day or two than most college grads do in a week. Many colleges can be converted to trade schools offering a college atmosphere with dorms, intramural sorts, etc.
If you are super lazy and super smart, learn to code. Sit around in a comfy chair in an office, or at home, with air conditioning and work like five hours a day while listening to music/movies and chomping on free food or slurping premium roast.
There are few things more satisfying that remotely listing to management drone on while you play video games.
Or you can learn a trade and stick your head in someones toilet.
I joke, sort of.
See my comment above re trades. I have a trade, a tech degree, BA, and a grad degree. I did most of it through distance learning. My son, another dumb tradesman (I guess), goes to work with a shop truck and laptop, provided by the company. He builds and programs autonomous driving heavy haulers, and does the electrical work on giant mining shovels. His salary is 200K per year, plus OT and all bennies because he is union. His workplace is respectful.
And just so you know, plumbers don’t stick their heads in someone’s toilet. They take the old one off and put the new one on if necessary. They will earn at least $500 per day to be honest and rarely if ever work on toilets. I’ve owned a home for over 40 years and have swapped out just one toilet. It’s not like they fail. Most plumbing is new construction, replacement hot water tanks, or leaking taps. It’s quite good work, actually.
The trades thing could be where the men are, whereas more older women are going back to college. that could explain the gender skew in the higher age brackets.
Or, learn finance, play golf & tennis with the right people and make more in an evening than a tradesman makes in a year.
once upon a time in America only well to do people went to college. Everybody else went to work to learn a trade. Maybe we’ll come full circle.
Ohio State was founded in 1870
Penn State was founded in 1896
I could list all 50 states – but the bottom line is that an affordable higher education has been around for 100+ years.
The real question you are asking is:
– Why are so many jobs that use to only need a HS education now demanding a college education
Population growth / (rate of full-time role automation+ full-time role outsourcing overseas) = a figure representing increased competition for each full-time position.
This relies on population growth being greater than the speed of destruction of well laid full-time roles. I think I am right about that. Otherwise, one would expect that equation to not work.
In addition, overall destruction of well-paid roles overall by outsourcing and automation increases the competition for those that remain.
My comments are badly explained. Please ignore.
“Why are so many jobs that use to only need a HS education now demanding a college education”
In the era of “everyone gets a trophy”, the secondary education system in the United States was dumbed down to the point that it’s likely not the equivalent of an 8th grade education offered in the 1960’s.
It’s also an easy, but arbitrary way for a hiring manager to winnow down a stack of resumes’.
The problem lies more in credential inflation than grade inflation. Employers demand unneeded credentials since they can. Because contrary to received wisdom, we already have an overeducated populace, holding almost twice as many degrees as truly needed for the available jobs. The BLS confirmed this with its own stats, along with independent academic studies.
The supposed “skills gap” mantra is just a way to dodge addressing longstanding structural problems of an economy that fails to generate enough high quality and high wage jobs. More education alone won’t fix this.
As I’ve said before, we don’t need better workers, we need better jobs!
Breamrod, I agree. My oldest son dropped out of college and went into an apprenticeship program to become an electrician. For four years he was on a pay ladder that saw him making above average wages from the get go. After four years he had his journeyman’s license and has never looked back. He had potential employers calling him! I have two master degrees and I’ve never made money like he has.
Cool. So, what you’re really trying to say is property taxes will go down? ;)
Good coverage once again Wolf!
The decade of warning signs to investors for anything touching Higher Indoctrination were present for all to see… lol
1) There about 10M students on this list.
2) Total student loans = $1,600M.
3) Total borrowers = 44.5M
4) Average loan is 1600M : 44.5M = 36K.
5) The average loan per student grad in 2018 = 28.6K (???)
6) Only 57% of students who grad in 2018 had debt.
7) There about 10M students on this list. 10M x 0.57 = 6M will have debt.
8) 6M students carrying debt, on this list, graduate, say, every 3-4 years, or 2M/year.
9) There are 44.5M borrowers. The turnover is 44.5M : 2M = x22 times in the last 10 to 15 years.
10) Something is wrong !!
May sound crazy, but why send your kids to college to waste their best youth years in order to become a corporate wage/debt/healthcare policy slave when you could instead give them each $1 million in early inheritance, and the fed will guarantee a 7-20% yearly return, so $70,000 to $200,000 income taxed at only 15% capital gains instead of 33%? And worste case, during a 100 year recession like now, you have only a two month correction that bounces to highs on $6 trillion of fed market bailout. Seriously, seems kind of silly to go to college if you have assets in the fed controlled markets that are too big to fail.
Just a thought…
During the 3 months it took to get 100K COVID deaths in USA, there were about 10x that many deaths from the other normal causes.
Population’s about 320 million people, life expectancy about is 80 years, so 4 million deaths per year. 3 months is 1/4 of a year, so about 1 million deaths…
COVID’s a big problem, and we definitely needed to take public-health measures to protect the medical system, but now it’s not a showstopper.
Big question now is can we get the kids back to school without causing a second surge…
One thing I noticed is during a recession, less students drop out of school because there is no other place to drop into.
\\\
I could write whole aricles on this topic, but in short…nobody cares. Really, nobody cares about the student or the quality as long as they get the check. It’s a money grab. The other 10% that do care are too few and too low to make ay significant change. This was inevitable.
\\\
You should write an article about it :-]
Don’t know how some of these institutions, some even older than the Republic, have gotten by all these years without selling off the rights to securitize their residence halls.
The question was raised above why so many positions require a College degree vs just a HS degree. Probably best answered by one of the VP of People types that became fasonable in the 90’s. Today we have VP of Human Capital to help guide the Corporate types.
Does anyone else remember when yo had the choice of attending a Vocational HS?
Yes, this one does remember Isl.
Actually a HS with both a ”college prep” and an extensive vocational program, and both were well regarded, with lots of the grads going both to college and to good working positions in the community.
AND, 1 ‘guidance counselor’ in a school with about 1100 students —– ONE!
A bright guy I knew in the class ahead of me had the focus in HS to be a barber; ran into him when I returned to hometown for a job 30 years later; he had gone from HS to barber school, then a couple of schools beyond that, done his military service, came home and set up his own shop and by then, ( after the ”old downtown” went down for a while,) owned the block his shop was in on the main street rapidly ”gentrifying.”
Retired early when he got an offer for his shop he couldn’t refuse, and was a multi millionaire by then. Of course he was also still with the girl he ‘went with’ in HS, and married when military service was finished.
Guess I was working too hard to pay attention when this concept of everyone going to college came to be, but it is quite absurd IMHO, other than the general case of becoming educated for personal growth, and that is easily done by reading a ton, as SO many people have done.
The only legitimate reason to go to college is to take a series of classes where, in addition to a long line of prerequisites, there must be labs as well as in person ”bull sessions” that bring out one’s intellect and refine it in the fire of immediate verbal challenge, though the net is definitely providing some of the challenge these days if you look for it.
Part of the reason is that public schools used to offer vocational tracks – at a time when almost all factory jobs paid a living wage for semi-skilled labor – and the academic tracks developed skills – writing and critical thinking – that many colleges today don’t achieve.
That’s what happens when you live in a post-literate society, as we now do.
The US was a far more literate country seventy-five years ago, despite far fewer people attending college. Re-read the speeches of the Presidents at that time, Democratic or Republican, and you’ll be bowled over at how dumbed down political discourse and use of language has become. In most fields, a college degree signifies (non-technical) skills equal to those of a high school grad decades ago.
My local JC is running ads on TV. Recessions are typically their busy season. People go back to school. The education mill has provided the JC system with higher credentialed faculty, PHDs instead of Masters. (at higher salaries) Mine has set up a network of satellites, (at no small expense) to make commuting easier. New staff sees pension funds are back loaded and fund assets are less likely to grow at the same rate. CalPers has shown in a test case, that opting out is a district by district decision (and JCs can cut labor costs, opt out of the pension fund, in order to pay the PHDs). JCs may become more competitive, maybe even doing the full four years, since the only real education you get at a major institution is post graduate. When the kids left college and went home a lot of them will stay there.
re: “Enrollment in private for-profit colleges has collapsed since 2011.”
This is a good thing.
My SO got a degree from Phoenix ‘University;’ prospective employers just laughed at it (as did I when in hiring manager capacity). I try not to bring it up, though, as she worked hard to get it and is proud of it.
High schoolers are hood-winked into thinking a college education/indoctrination is the be all to end all. Outrageous tuitions support outlandish salaries and benefit packages for professors and administrators, who laugh all the way to the bank. It appears most college students today are ill equipped to secure gainful employment and quickly realize a degree in partying 101 will only net them minimum wage jobs. Conversely, had they attended a trade school, many prevailing wage jobs pay upwards of $90 per hour.