It gets serious. Margin calls?
No one knows what the total leverage in the stock market is. But we know it’s huge and has surged in past years, based on the limited data we have, and from reports by various brokers about their “securities-based loans” (SBLs), and from individual fiascos when, for example, a $1.6 billion SBL to just one guy blows up. There are many ways to use leverage to fund stock holdings, including credit card loans, HELOCs, loans at the institutional level, loans by companies to its executives to buy the company’s shares, or the super-hot category of SBLs, where brokers lend to their clients. None of them are reported on an overall basis.
The only form of stock market leverage that is reported monthly is “margin debt” – the amount individual and institutional investors borrow from their brokers against their portfolios. Margin debt is subject to well-rehearsed margin calls. And apparently, they have kicked off.
In the ugliest stock-market October anyone can remember, margin debt plunged by $40.5 billion, FINRA (Financial Industry Regulatory Authority) reported this morning – the biggest plunge since November 2008, weeks after Lehman Brothers had filed for bankruptcy:
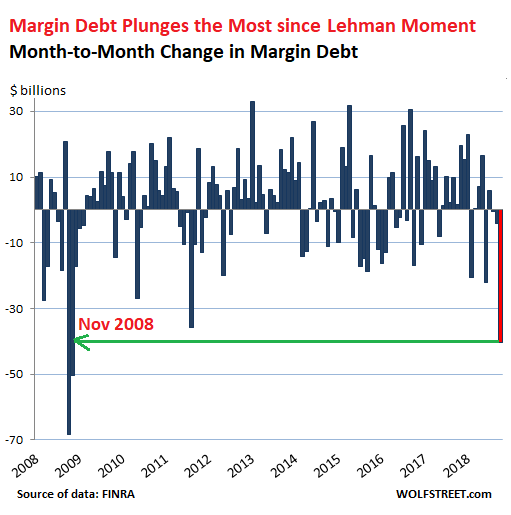
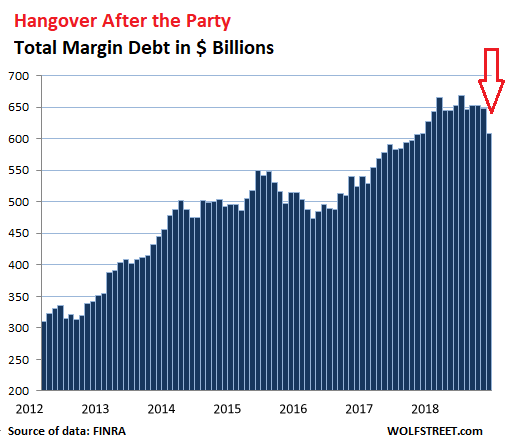
During the stock market boom since the Financial Crisis, this measure of margin debt has surged from high to high, reaching a peak in May 2018 of $669 billion, up 60% from the pre-Financial Crisis peak in July 2007, and up 117% since January 2012. Since the peak in May, margin debt has dropped by $62 billion (-9.2%). Note the $40.5-billion plunge in October:
In the two-decade scheme of things, the relationship between stock market surges and crashes and margin debt becomes obvious.
Back during the dot-com bubble, dot-com stocks, traded mostly on the Nasdaq, included what today are booming survivors like Amazon [AMZN], barely hangers-on like RealNetworks [RNWK], or goners like eToys.
At the time, these stocks soared by stunning amounts, and people, such as myself, used margin debt, to enhance their returns. When stocks plunged, the margin calls came, and these people had to sell their holdings into an illiquid and plunging market. They ended up selling their best and most liquid stuff first and watched their trash get trashed further.
When it was over by October 2002, the Nasdaq had plunged 78%. Over the same period, margin debt plunged 54%. A similar scenario played out during the Financial Crisis crash. And now we have the “Everything Bubble” to deal with:
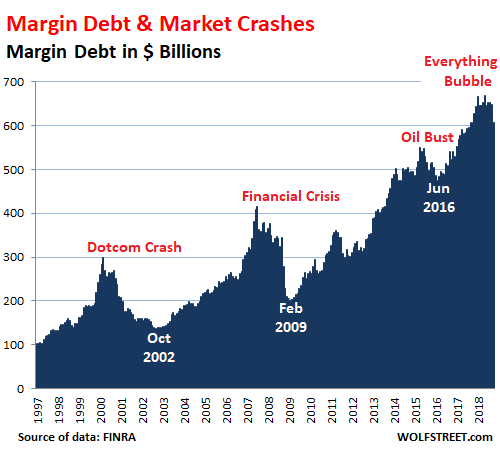
Surging margin debt creates stock-market liquidity out of nothing, and this new liquidity is used to buy more stocks. In this manner, rising margin debt is the great accelerator on the way up.
When prices on individual stocks drop sharply – even as the S&P 500 index might decline at a moderate pace – investors, including hedge funds, with margin debt and concentrated holdings in these stocks may find that their portfolio has taken enough of a hit to where they get margin calls.
Now they have to dump stocks to pay down margin debt. This begets further selling pressure, which begets more margin calls, which begets more forced selling…. In this manner, a high level of margin debt turns into the great accelerator on the way down.
But this money from those stock sales doesn’t go into other stocks or another asset class, and it doesn’t sit at the “sidelines” waiting to jump in again at the next dip. Nope, it is used to pay down margin debt. And thus, this liquidity just evaporates without a trace.
October’s plunge in margin debt was just the beginning, a little dimple in the overall chart. Unwinding such a huge pile of margin debt and overall stock-market leverage takes time, years, and they’ll be interrupted with some brief increases that’ll make everyone feel better for a moment.
It gets costly when the entire market depends on a handful of over-hyped mega-caps. Read… FANGMAN Stocks Plunge 4.4% Today, Down $905 Billion, or 20%, since Aug. 31
Enjoy reading WOLF STREET and want to support it? You can donate. I appreciate it immensely. Click on the mug to find out how:
![]()


The Cancer in the Financial system was was identified back in 2007. It’s now the time the doctor removes the disease, 12 years later. We are on the operating table and the camera is focused in. We see the operation unfold as the scalpel does its work in skillful hands. The aspect is Pluto square Chiron.
RoseBud, I haven’t even been looking at Chiron. What about Saturn moving in with Pluto over the next year? Forget the skillful surgeon, is this not the Grim Reaper coming to get us all?
Omg.
not sure Wolf wants his site turned into an astro-financial site, but since we are talking Lehman and the period around 2007/2008, I thought I would share an activated transit that mentions a scalpel.
Color me cynical. If Aerospace Engineers designed aircraft control systems like the financial system’s control system no airplane would ever get off the ground. A system does what it was designed to do. The financial system was deliberately designed to wildly overshoot and undershoot the averages. The better to fleece the muppets making some parties ever richer and richer.
oh you must be referring to the “behind the curve” reactionary feds micromanaging interest rates and money supply to counteract the “natural” business cycle. Are 3 rate hikes still on the table for 2019? i ‘m hearing some scuttlebutt. i am enjoying my brokered cd’s
” i am enjoying my brokered cd’s”
Did you ever look at the coverage ratio of FDIC?
They will cover at what cost to your CD’s
Erle,
Please quit posting this fearmongering BS on my site. Post it elsewhere. Or better, learn what “insurance” is all about and how insurance works. All insurance works on the same principle. No depositor insured by the FDIC has ever lost a dime, not even during the big-bad Financial Crisis when 11 or so million people lost their jobs, when thousands of companies went bankrupt, when countless people lost their homes, when stocks got crushed, and when conservative-sounding bond funds imploded. But no FDIC-insured depositor lost a dime. How hard is this to get?
The ancient Middle East knew how to run a control system for their economy, eg, Egypt, Sumer, Judea. Preriodically forgive the debts or see your economy crash every 30-50 years.
The Greeks thought they knew better, and introduced democracy as a buffer between creditors and debtors.
It’s gone downhill ever since
I have an account at one of the large self-serve brokers and the margin interest rate is about 8%. You’d have to be pretty confident in yourself to take out a loan at 8% to buy stocks. The stock would have to return 8% just to break even. The brokers are making a killing off this. Maybe not as lucrative as the credit card business though.
You know the cycle is near its end when the lucrative business stems from loan-sharking behavior. It won’t take long for the hapless individuals to lose all their money. The source of these easy profits quickly evaporates. It’s not a long-term sustainable profit source.
That’s you. I imagine institutional investors have access to better rates.
The big brokerage firms Ameritrade, Schwab, Etrade, etc all spend plenty on TV, Internet and print ads aimed at the retail investor. But as Bobber points out, they are charging 100x the rate they pay on free cash in the customers’ account- that is price gouging, plain and simple. It used to be that the broker loan rate was about the best you could get because of the 50% margin requirement; furthermore they are free to liquidate your stocks instantly if your shares drop, unlike a bank dealing with a mortgage-holder in arrears.
What I have never seen mentioned is that, knowing the positions of their customers, they are in a position to borrow their own customers’ funds pretty much interest-free to short their shares, and to do so when they have their backs to the wall.
They also sell their customers data. Winning!
You go in knowing the rules and rates. That is how any business is ran and why contracts exists to know the responsibility of the parties involved. “Price gouging” is not the correct phrase as there are 100’s of brokerage firms with lots of competition. If you do not like the rules or rates, then negotiate for what you want or shop other providers or invest in markets that are less retail and closer to wholesale, such as real estate or invest in start-ups directly; more work for the investor with greater risk.
We all know many self-made millionaires that have increased their wealth by the retail brokerage house as well as the providers of the riskier boutique type brokerage firms that invest in small retail projects and start-up companies.
my brother in law by marriage is day trader since 2000 in Australia.
He was using small cheap broker to do trade and in 2008 his broker go bankrupt.
You can read on wiki :
Opes Prime Group Limited was an Australian securities lending and stockbroking firm which suffered a dramatic collapse in 2008.
Opes Prime trail-blazed a unique form of margin lending backed by stock lending agreements. Investors handed over legal title to their share portfolios in return for money to buy more shares. When the broker collapsed, the fine print of those agreements meant ANZ and Merrill Lynch, another financier, had complete control of investors’ shares.
The banks sold off the shares, along with a collection of Maserati and Ferrari cars that had been imported by the directors under a side business, to recover their own debts. Investors shouldered $630 million in losses.
https://en.wikipedia.org/wiki/Opes_Prime
Yes. over here it happened to CEO Dr Anthony Soh of Jade technologies. Merillyn Lynch liquidated his entire equities holdings without him even knowing.
Remember the old Wall St. saying: The bulls make money, the bears make money, but pigs go to the slaughter.
Once upon a time (early 2000’s?), the margin rate charged by brokers was much closer to the Fed funds rate and even a small borrower like me could buy a bond offering on margin knowing that I could repay the loan with an upcoming bond maturity. There was a positive carry. Since start of the Great Recession, such trades don’t make any sense. My guess is that the brokers are doing well with their margin loans, but the drop in stock commission rates has been good for me and I have not used margin for over a decade.
Free tip: Remember the days when successful stockbrokers (now called wealth managers?) were given big incentives to move to another brokerage firm? These days, customers can ask for moving bonuses as well. Check out this web site for recent bonus levels and you may be able to negotiate something better: http://www.hustlermoneyblog.com/best-brokerage-bonuses/
“You know the cycle is near its end when the lucrative business stems from loan-sharking behavior”
Bobber,
Consider PayPal lucrative? They now charge a punitive 1% for money removed from one’s account to any instrument other than a bank account…they REALLY want bank account access…credit cards, no good.
Why are they forcing this issue?
Sadly, those who utilize margin debt, have voluntarily “invested” in nothing more than another Wall Street wealth transfer scheme…
Does anyone know any investor who has used credit cards to buy stocks without the funds to repay, in short banking on stock rise to pay off the amount owing on card?
Surely, this isn’t done. Might as well go see Guido down at the Bada Bing. Webistics. :-) (Sopranos reference)
That was a huge chunk of the crypto boom, until it was disallowed.
I had a grad student friend, who in February 2009, took $50k in cash advances (0% teaser rate at the time) from credit cards that he opened at the time. As he put it, if Goldman can leverage their balance sheet 30-to-1, why can’t I? Figuring the market was close to bottoming and that the risk/reward was on his side, he bought into a handful of heavily depressed individual securities, lost sleep for a month as the market bottomed, and struggled to roll over the credit into new cards 6 months later. A year after, he was sitting at $250k – long term gains.
For every guy who got lucky and the timing worked in his favor, there are 99 who lost it all. Just like a casino. The losers don’t go around telling stories about how they foolishly lost everything and a lot more they didn’t have.
A lot of people do very well doing crazy stupid stuff with money. But glad that worked out for him. Would have been a rough pit to crawl out of.
The Canadian term ‘hoser’ comes from hockey whereby the loser has to hose down the ice rink after the game.
CANADA is filled with hosers smart enough not to bet on credit card margin debt at 28% and counting.
I’ll bet that same guy is now on the street picking up pennies in front of steamrollers for just enough to buy a lottery ticket.
MOU
Sadly, the margin and other debts will accelerate any downward spiral as any decline will result in margin calls or the unavailability of loans to refinance securities holdings and other leveraged investments.
I am amazed the economy has not done worse.
Legalized gambling. Nothing more, nothing less.
Carnival of comic deceit, flim-flammery & creative rigging. Why continue to call it a market ? There is a free market out there somewhere, but the licensed rigged casinos, whose valuation indexes are constantly referenced as market reality, only promote further mass delusion, and serve as part of the wealth & credit transfer scheme we face.
Something like 70-80% of market volume is already HFT algos buying and selling to each other in fractions of seconds. The big trading firms can use AI and their awareness of retail investor muppet positions to rig and manipulate markets and fleece the muppets, while captured and complicit regulators and enforcers turn a blind eye. These “markets” are nothing more than a rigged casino intended to loot and asset-strip the wealth and assets of the proles. The Fed and its bankster accomplices are exactly what Thomas Jefferson warned was going to happen to us.
Seems like a mix of gambling and a pyramid scheme to my less-than-knowledgeable perspective. I won’t pretend to truly comprehend much I read about the world of finance but the more I learn the more I feel like it’s a scheme for a few to get rich off their promises to the masses of the wealth awaiting them if they just keep buying more.
It’s no accident that the Fed’s monetary policies over the past decade have resulted in the unprecedented concentration of wealth in the hands of our oligarchs and widening “wealth inequality”, while the middle and working classes are steadily losing ground.
We will not have sound money or honest markets until we end the Fed.
“… people, such as myself, used margin debt, to enhance their returns …”
Am I the only reader surprised by this? It always seemed that Wolf was a very conservative investor (I’m too chicken to short, much less use margin although I have a margin account).
I share your thoughts concerning Wolf, it was in my thoughts during my first reading on my phone. Too much effort to comment on an Iphone5 much easier now on my laptop. I will look forward to Wolf’s response, my guess, lesson learned, share the experience, and pass it on.
California Bob,
You live and learn. I lived and learned. In fact, I did two things simultaneously back in 1999, that both ended up being very painful:
1. Because I saw the crash coming, I shorted the highest-flying Nasdaq stocks in October/November 1999 and lost so much money in such a short time that I still get dizzy when I think about it. Timing was off by just five months.
2. Instead of just getting rid of all my stocks entirely while I was shorting specific highfliers in late 1999, as would have been logical, I kept them on margin, thinking that they would do just fine in the coming dot-com crash (Biogen, Dell, Intel, etc.). They all survived, but at a fraction of their dot-com highs. Some of them I was forced into selling. Then I had a couple of stocks that turned into trash right there in front of me because they were hard to sell because there were no bids.
Live and learn. By 2005, I considered housing in a total bubble, and by late 2006, I saw the cracks in the financial system and feared that there was a lot worse beneath the cracks that I couldn’t see. So I got out of stocks entirely (lesson learned from the prior crash). This was a painful year too early :-]
I’ve traded through three crashes in my life: 1987, 2000-2002, and 2008-2009. After a while you see this shit coming. But that doesn’t mean you get the timing right, or that you don’t screw up in some other way.
I still take risks. But I try to be fully aware of them, and I want to be paid for taking those risks. I NEVER chase yield. That’s the single most expensive thing anyone can do. I hate open-end bond funds; they sound conservative, but you’re gambling that there won’t be a run-on-the-fund, and you’re not being paid for that risk, which is real and deadly. These instruments routinely blow up during a bond selloff.
By now, I’m essentially a pile of lessons-learned with legs.
In this deflating Everything Bubble, capital preservation is my guiding principle. I don’t trade anymore. I can’t stand sitting in front of four neurotically blinking screens the way I would have to if I tried to trade these crazy markets. I have a business to build (WOLF STREET) that takes up every waking hour of the day. I’m having a blast doing it. But that too was a big risk when I started it because how the heck are you supposed to make money with this?
Turns out, I figured it out, and it’s doing great, going from record to record, thanks to my awesome readers and commenters.
The funny thing is that the potential safest thing to do now is to have everything in cash or gold. Then wait for the crash and go bottom fishing.
But as you pointed out, the problem is always going to be timing. There is no guarantee that the market would not go up from here to the end of the year, or even longer. Then you have inflation eating away at your cash. This is improbable, but possible, for example, the trade war with China ends, our government start to function correctly instead of endless politics, the Fed slams on the brakes and kills all further interest raises for 0219, Brexit suddenly turns smooth and everyone in the deal becomes a winner…. and so on.
Then when the inevitable crash occurs, there is no way to tell when the bottom is or who might be left standing. Amazon might suddenly turn into the Microsoft and Intel of 2001. Sure, you could mitigate that risk by buying into ETFs, but the timing is going to be very challenging. You can see the market fall 20%, then flatten out, and thinking this is a perfect time to get in, only to have it fall another 50% due to some type of external shock.
Wolf thanks’ for that anecdote, it was really cool! I am going to save it for future reference. I made money in the stock market then I started using margin loans cause I wanted to be like Jesse Livermore. Greed and my ego took over and I went down faster than a hog eating swill!
Wolf Street is Cool!
If you really want to toss some money away, try timing 3x leverage exchange traded funds. Decay is a killer.
If you can turn YOY returns of 10% into 30%, what’s a bit of vigorish?
Being early with 2x and 3x ETFs + Decay = painful memories.
Thank you for your transparency Wolf. It’s so easy to compare one’s “Google” life to others’ “Instagram” life.
I know you know this, but GenX got hit hard. We graduated into aftermath of the twin recessions of the early ’80’s, got “downsized” repeatedly (the entrenched boomers stayed, the recently hired GenX went). Then when we found ourselves working at the gas station, it was because we were slackers, not because of any real macro trends or policies.
Just when we got a little saved up during the ’90’s, *poof* — dotcom hits. OK… so save up a little more and buy a house circa 2005. They’re solid, right?
These days, we make great tax donkeys. Not enough wealth to avoid taxes, but just enough to tax to the rafters. While the boomers form their LLC’s and family trusts with the money we paid for their overinflated houses, we’re left … paying for the houses.
My theory is that GenX is the Other Silent Generation. Too busy — and ashamed of — hanging by a thread to really talk to each other about it. I’m proud of my serial recoveries, but I don’t talk about it much. There’s always some boomer ready to shake their finger at me and tell me what I shoulda coulda…
And the last thing I’ll ever do is invest in a market whose animal spirits are controlled by a type of herd thinking I’ll never understand. I’ve learned that if it makes no sense to me, everyone else will pounce on it, and if it seems logical and prudent, everyone else will assiduously eschew it seemingly forever. So there’s an ocean of “makes no sense” options whereby the best analysis tool available is a dartboard.
I seriously doubt I’m alone in this dilemma. I read your site to keep track of macro bombs so I can do my best to position my family out of the blast radius.
I’m not interested in riches. I just wish the people who are could be content at some point (not going to happen) so they wouldn’t have to cast a greedy eye at the cash flows I produce, trying to figure out how to illicitly (legal or otherwise) cream some off the top for themselves for nothing in return.
@MF-
You must be thinking of the early boomers.
The late boomers missed-out and share the pain with Gen X.
Not every boomer is livin the high life showering in $$$ …
Many of us are squeaking by hoping not to get devoured by inflation, taxes, and corporate greed !
MF
Very interesting narrative. Sadly Boomers are not all doing as well as you may imagine. Many of us hit the same troughs you did. We just added the oil shock recession of the early 1970’s. That was a fun job market to graduate into. The best thing I can suggest, don’t be reactive. When a SHTF event occurs, the worst damage will happen before you know about it.
I feel you, MK. Borderline gen x / millennial here. From Europe, now in Silicon Valley. Same experience. Been super thrifty all my life, serial saver, and not without achievements, only poorly compensated in asset terms and with little hope of doing anywhere remotely as well as a mediocre college grad of the 60s-70s. Boomers never did a thing right, their success wasn’t theirs, they squandered it all: rights, protections, standards, wealth and security that they never earned, sold the future for instant gratification. That was the hook they swallowed, corps figured them out and played them. Even today they are the last consumers standing, feeding on & the machine, still getting out to vote for the old con guard. They can’t stop, they won’t stop, they’ll never admit and never face what they did. Champions of personal liberties? They were hypnotized into everything. Sex drugs and rock and roll: that’s the accomplishment? Those were emerging industries with mature psyops. Gay rights? Sure, cute. But who forgot about colored people? And the working class? And the environment? To name a few. The generation that took from their parents who came out of a war or two and who lost it all for the next. What do we have to look forward to now with social institutions, work environment in shambles, inequality rampant and entrenched and climate out of whack and spiraling ? We’re the ones having to swim upstream, breaking a sweat just to stay in one place after they’ve been floating jolly downstream for a lifetime. And yeah, I know many boomers have wound up gasping for air on the shore, still more have it coming, if they live long enough: inflation is the reaper when you have no control over your income. It is also a godsend for younger student loan debtors (I dodged that one) and all other debtors. Which is why the Credit-Controller EU fights it so vigorously. I value Michael Hudson’s perspective: https://www.nakedcapitalism.com/2018/11/michael-hudson-moral-hazard-vs-mutual-aid-bronze-age-saved-debt-serfdom.html
In Late Stage Ponzi Capitalism [see Minsky] Keynesian illogic reigns paramount to rational pragmatic players in that markets can remain irrational longer than you can remain solvent. Greed is part of the game in Late Stage Ponzi Capitalism whereby stackers & speckers alike are singularly motivated to get more.
Some like Richard Fuld never know when to quit ahead of the game when they start to believe in their own ‘rationality’. If you have skin in a market that is based upon Keynesian irrationality it is best to bet on the irrationality and to bet against the rational pragmatic investor because the so-called rational investor is not really rational if he/she is in an irrational market. Buffett has taken his money off the table in expectation of a market crash. Our host Wolf is also out of the market.
No market player is an island unto his/her own interconnected investments whether RE or small business.
Not following the irrational herd is irrational lest they run you over when they bolt for the exits all at the same time.
MOU
Thanks for being so forthcoming, Wolf. Myself, I’m counting on diversification to survive the coming apocalypse: I have cash in an IRA, cash in a brokerage account, cash in savings and cash in a CD. How’s that for diversification?
You might add one thing, a small position of economic insurance, 5% or so in gold and silver.
There is even a risk in cash, as the Germans found out in 1923:
http://www.pbs.org/wgbh/commandingheights/shared/minitext/ess_germanhyperinflation.html
I still have a 20 billion (milliard in German) Reichsmark stamp which I probably bought as part of an offering in the book of a comic book some sixty years ago. Ten years before that stamp was issued, a Reichsmark was worth about 25 cents US under the old gold standard.
Recommended reading: Barton Biggs, “Wealth War and Wisdom” 2008.
Those who don’t learn from history are destined to repeat it.
“book” should be “back”.
California Bob,
How is having all of you assets in cash a good thing? How do you protect yourself from Inflation? You should have at least 10-20% of your cash in Physical Gold/Silver. I’m sure Wolf would agree.
I exited stocks completely in ’99 and bought bonds. Friend of mine was CEO of a small brokerage company and I ran into him a few months later. When I told him what I had done, he said I was crazy to buy bonds at my age. I thought, what do I know?.. he’s the guy running the brokerage house …so I bought back in having missed several months of the blow off top only to buy in just before the collapse. Bonds went on to make a decades long run. That decision cost me 5+ working years and created lots of scar tissue.
Thanks for sharing, WR. My son always learns his life lessons the hard way. Pick a topic and put Sam in the header. He mentions it often with a rueful expression; cars, girlfriends, etc. Thankfully, he has stayed away from stocks. So far.
Rules to live by:
1- There is no “stock market”. In it’s place there is a casino with the rules designed to benefit the Real Players. It’s original purpose—- to provide a mechanism for price discovery and provide funds for investment to create products the society needs—– is as quaint as a flip phone.
2- Humans are herd animals. Their species behavior is fundamentally delusional. They have short term memories driven by the more fundamental drives of power, greed, and sex.
If you enter the Casino without completely understanding these facts you will be relieved of all your cash suddenly or gradually. Just like you will physically be thrown out of a Las Vegas casino if your style of play is identified as a winning one.
In my younger days I taught myself to play system Blackjack for amusement and profit. I could play all seven decks of a table continuously and keep a running count of the odds vs the House for each hand without missing a beat. No mathematical genius involved— just a bit of practice. With a initial stake of X, the odds of loosing the entire stake were exactly .05 the maximum individual bet. When the deck is favorable you can play with a usable advantage over the House. Luck has nothing to do with it— just basic mathematics and self discipline.
When I enter the stock market casino I wouldn’t dream of trying to time the market, fish for Carp on the bottom, identify the next Microsoft, gamble on shorting the House, or delude myself into thinking that I’m “investing” in the future. I like to sleep at night, so I rarely hold a position overnight even if it shows no red flags. I’m a seller, not a buyer. I cover my position at the same time I initiate it. Leverage with security. As an option seller I have time on my side, momentum, liquidity, and most important, human psychology.
I used a simple count method to play blackjack too. While shopping for my first home decades ago, I lost a few hundred dollars in a casino over the course of an afternoon – even though the “deck was favorable.” In those days that few hundred dollars was about half a month’s mortgage payment.
So I stopped gambling at the blackjack table and promised myself I’d never play again until I owned a home free and clear. Funny thing is, my home’s been paid off for eight years, but I’ve not played since that day.
7,8 & 9 = zero
2,3,4 & 6 = plus one
5 = plus two
10, Jack, Queen & King = minus one
Ace = minus two
The deck’s count influences decisions on whether you hit with a twelve or thirteen vs the dealer’s up card, whether you split or double down and how large you bet a hand before being dealt.
The system works well in a one or two deck shoe, but not so well in a multi-deck shoe. Plus, the dealers for the most part do a great job shuffling the decks to keep an even distribution of cards and that makes it harder to use the count to beat the house.
Since 40% of my portfolio is in equities, that’s more than enough gambling I reckon. I hope you win at the stock market casino Crazy Horse!
Hi Dan
It is almost impossible to win long term in the Las Vegas casino once the casino learns that a skilled player is at the table. They will shuffle your advantage away or simply kick you out. Bear in mind that this was 40 years ago. Back then the only casinos I encountered that would allow skilled play were in Cartagena Colombia where they dealt face up from a 4 deck shoe and I could play hundreds of hands an hour. I never had a losing day and never was cheated or physically threatened like I had been in the US. It’s not about luck— just simple mathematics.
The point I was making is that gambling at casinos is for suckers and fools. It’s only benefit is the lessons it teaches. One of which is don’t gamble (so-called “investment”) in bigger casinos like Wall Street unless you can hedge your bets, understand the psychology of the herd and the mathematics of odds.
That was a great recount wolf. You rock. I started trading in the dot com era when it was hard to make a losing trade, especially if the trade contained the acronym IPO. Fully margined, jumping from risky to risk, trade to trade. Invincible. Or so I believed. You can imagine the rest of that life tale. I survived. Barely. Years later and a little wiser I remain a market addict but trade just on the side, enough to satisfy a pleasant addiction. A newcomer to your blog…I love it. Here’s to many more market years. ~v~
Thanks Wolf. I retired in mid 2008, and wanted to invest a chunk of money. Half went into something I knew from my career, the other went into a huge company that had a ton of analyst coverage and a buy recommendation from a Ratings Agency. I flagged up something to give a “sell” flag, (which I later ignored.)
That company was RBS.
It took me a year to trade out of that mess.
The first chunk of investment paid off very well, all considered.
If you invest, first decide where the exit is, and do not forget it.
Analysts look at a lot of factors in a stock, but they never look at what really affects the stock price the most. They should be looking at how greed and fear drive the behavior of large groups of humans.
You have to remember there were plenty people who believed that the Internet was just a toy which would be hard to monetize. And that the most promising technologies would be subsumed by traditional businesses. It was radical and visionary to suggest that it would have to be the other way round, e.g. to harness the potential of the Internet you had to be an Internet company first. After you won that battle you could buy the pieces of the traditional economy that made sense. Knowing that gave you the key to exploiting a once in a lifetime opportunity to become rich.
And some people did. The problem, as it always is, is picking the right ones at the right time. Traditional thought was that *if* indeed the Internet was a paradigm changing emergent industry, then the best companies would be the first ones that established themselves before the get rich quick 49ers. That was true with Amazon, but Google didn’t IPO until well after the bust, and every single social media company flamed out, leaving Facebook the last man standing. Jobs willed Apple into market space its now in with one foot one the Internet and the other in hardware/software, that would have been difficult for anyone to picked in 2000. But in general, the trail blazers weren’t reliably the ultimate winners.
But, if you did select correctly the dot.com 1.0 boom *was* a once in a life time opportunity, and leverage would have been indispensable to taking advantage of it. There’s no shame in having improved your odds for becoming a multi-millionaire stock investor from 1 in 10,000 to 1 in 12 through your market research and technology perspective, but still ended up rolling snake eyes. (At least as long as you didn’t make your children go hungry and shoe-less to do it.) Wolf is just unusual in having admitted it failure.
@earl d
Obviously You are correct in that if you pick the right stocks you are going to win big, but that’s very very hard to do.
Here’s an example as to how hard: during the dot.com boom there were a lot of smart tech people working at a lot of cutting edge companies. Most likely even these inherent insiders would not be working at X company if they thought Y company was better, correct?
Thus Is complete outsider : retail investor better able to tell whether X is valued correctly relative to Y? Of course not.
But there is an easy solution. If you believe in sector / industry, just by the sector fund and let nature ttake its course.
Yes, you will have smaller gains than if you picked only the winners. But by going with the sector fund you no longer have to be a trader / analyst on a day to day basis. Making this change significantly decreases the risk that u will miss out on the big move / get head faked by strong hands with big money. Or simply manipulated to sell by bad fake news about ur favorite stock.
Rathe the sector and keeping reading postive stuff about the industry as a whole. This will help you maintain your position/ stick to your convictions
Obviously don’t brainwash yourself, but IF you’ve developed a solid idea / concept, your main problem going foward is gojng to maintaining the position through thick and thin.
No one gets Rich by quitting on good ideas when the gojng gets tough. But it is very very tough, IMO,to stick with individual companies through thick and thin, given the flood of manipulative information about individual stocks.
That’s one of the main lessons I’ve learned in the past 30 years of market watching / trading/ investing.
And Reading the best sites out there, like wolf’s, is a great way to stay in your trade/ hold ur convictions for the long hay.
I don’t disagree with any of your observations and I certainly would not have suggested that anyone invest in the dot.com boom (bubble)
But I would add if you have real insight into an industry, company, technology that the broader market doesn’t have, and you are a thoroughly knowledgeable, disciplined investor you can assemble and manage a portfolio that performs better than the market, even quite a lot better. The above are very rare qualities, and a given individual is usually not able to make the above determination for themselves, i.e. if you’re not knowledgeable it’s often quite easy to convince yourself you are. But it’s certainly possible for the non-institutional investor to acquire the needed knowledge skills and discipline, and sometimes being an outsider gives you a superior vantage point.
Two examples:
1. It’s been quite obvious for the last 5 – 7 years that renewables, wind and especially solar pv (see Swanson’s law), were growing at a geometric rate and their costs were steadily declining and this would continue into the next decades. That meant that even though solar PV constituted only a minuscule portion of world-wide power capacity (in 2012 about 0.5%), that soon it would first dominate new power additions and then begin to strand existing fossil fuel (gas and coal) assets. Now, just 6 years later solar pv accounts for ~2.5% of world-wide capacity (end of year 2018E) and renewables account for 70% of new power additions. That insight was not shared by leaders in the power industry who were paid multi (10s and 100s) millions of dollar to have exactly such a knowledge. GE alone has lost $10s of billions in their power division due to the their collective ignorance, and it’s hard to see how the company can survive the fact that sales of their gas turbines (and associated service contracts) are tending toward 0 in the foreseeable future.
2. There is a whole vapor-ware industry predicated on the fact that fully autonomous vehicles would already be commercially available. There are an ocean of highly intelligent computer science Phds fanatically convinced of that. Yet, it has been completely obvious that such a vehicle (where you setup a remote desk and xbox station in the back of your suv and work as you car drove you to your office) was decades away, at best. Even such basic activities such as finding a parking spot and parking at the local Whole Foods not only aren’t solved, there’s still no generally agreed upon plausible approach to solving them. Musk had ‘promised’ that Tesla’s self driving software would already be activated and being sold in new models. In fact there was a preorder option. However, not only has the software not been delivered, but the preorder option has been removed when buying new vehicles, and company estimates from the company have gone from:
Any day now, the software’s ready we’re just polishing it so it’s perfect
to,
Not in the next fiscal year, at least.
If anything the stampeding herd mentality has become characteristic of our social media age as has the counter-stampeding conspiracy fueled, contrarian crank.
Are there any estimates the extent to which SBLs have been utilized to purchase other assets (art, real estate, etc.)? Or is it reasonable to assume that SBLs are predominantly contained within the securities markets?
@Bobber, there are retail brokerages, such as IBKR, that have dramatically lower margin rates.
Sad. After the Dot-Com crash and the Financial Crisis crash, people don’t learn and make the same old mistakes.
Here’s my rules to avoid this mess;
Do not borrow money to buy stocks, or use financial investments for collateral.
Be very wary of any advice given by a commission based salesperson.
If you don’t FULLY and COMPLETELY understand an unusual investment product, don’t buy it. The promised, but never guaranteed, returns almost never happen for you, but the broker always gets the full commission up front.
Have your investments in a boring, diversified portfolio with enough cash to avoid having to sell your boring, low cost index based stock funds at a loss. You won’t have returns to brag about, but will avoid losing everything.
Don’t Panic. We have been through this mess before.
The gross amount of margin debt is up, but the overall stock market went up too, so these numbers are correlated. Luckily, as long as the inflation is “too low”, the FED has nothing to worry about.
This time it may not be just margin debt. I recently got this message from my broker:
As the Branch Manager, I want to make sure you know about a new way you can draw on the value of your portfolio without selling assets: the *** Line of Credit.
Using an *** Line of Credit, you can access cash when you need it without disrupting your long-term investment strategy. By pledging the assets you hold at *** as collateral ($200,000 minimum) you can access up to 50% of the value of your eligible investments. You’ll also enjoy:
Low rates, no hidden fees. Only pay interest on the amount drawn.
Flexible draws and payments. Access your available credit online anytime, and choose from monthly payment options, or defer payments with interest rolling into your principal balance.
If you’d like to learn more about how an *** Line of Credit can help address your immediate financial needs while keeping your investment plan on track, please do not hesitate to contact me at ***.
Thanks again for the opportunity to help you with your investing needs.
Mr. Knoss,
Thanks for this illustration. This is a perfect example of an SBL (securities-based loan) that I mentioned in the first paragraph, and it’s also a perfect example of how they’re being marketed, and how hot they are.
My brokerage offered me that. They give you a checkbook. (Just like the one Treasury gives the FED!) He also assured me that if the stock market corrects (and my assets lose value) they won’t rejigger the topline number, causing a margin squeeze. So its more like a HELOC in that regard. You didn’t mention, in my PLOC I cannot buy more stocks with them. (However I can write a check to another brokerage, which I think frankly is not in their best interest). Now if I deposit the funds with the new broker in cash, will they write me another PLOC?
“But this money from those stock sales doesn’t go into other stocks or another asset class, and it doesn’t sit at the “sidelines” waiting to jump in again at the next dip. Nope, it is used to pay down margin debt. And thus, this liquidity just evaporates without a trace.”
What an inefficient and unproductive use and waste of capital.
My schooling was from The School of Dot Com as well. They never taught us this stuff at the university:(
A “margin call” is a pay your debt demand – NOW.
Imagine if this was the case with household debt!
The US household debt has hit a new record high of $13.5 trillion.
This is $837 billion higher than the previous high, which occurred just prior to the 2008 crash!
Student loan debt is over $1 trillion.
Credit card debt is approaching worrisome levels of defaults.
Debt. Debt. Debt. As far as the eye can see. What can go wrong?
Curious to see how much worse the November drop will be.
Is this margin debt the driving force behind the steady sell off in the market this month. Dow and S&P since the 8th, even Bitcoin has taken huge hits since the 14th.
November has been a sell month, it started off fairly smooth. Not sure what was the catalyst that lit the match after the first week. Might be a rough December.
Please Sir, I want more?
The outright audacity!
Sears Holding Corp. has asked the bankruptcy court to approve millions of dollars in bonuses to 18 company executives.
The beatings will continue until moral improves.
Bonuses for what? From the beginning, it was pretty obvious that Eddie Lampert would suck out all the equity from Kmart’s real estate, then blame the failure on ecommerce.
I could have done that for 1/10 the cost.
Eddie Lamprey
I’m really surprised that some of these principal jackals … oops … I meant principaled execs, haven’t been ‘taken out’ by angry and disgruntled marks ..
It’s amazing to see this level of chicanery at the top, without ANY repercussions what-so-ever !!
By implication the shorts (shorts are 100% on margin) are getting busted out of this market, which means?
Wrong, obviously.
Shorts don’t take the market down, a short always involves a promise to buy, (and it is a third party transaction) if the stock exchange were more like a commodity exchange then the shorts would have leverage. Selling drives the market lower. Short interest never begins to approach downside volume (used to be you had to short on a uptick). There are a number of ways to squeeze the shorts and margin is one of them, controlling the float is another, and outright ban on short selling is another. Best guess is SI came off during November, some of it was profit taking.
Wait, is this just a bastardized form of fractional banking? Isn’t money created just because the market capitalization increased?
Buy stock
Price goes up (for everyone).
Margin credit goes up because collateral goes up.
More people buy the stock
Price goes up.
Rinse and repeat.
\\\
This is nothing new, but here goes:
\\\
If I were a “broker union” and needed to get rid of large number of stocks without creating a mass sellout I would:
1) Incentives stock purchasing and speculation by providing liquidity (Excellent example provided graciously by Mr. Knoss).
2) Find examples of companies doing good, and over exaggerate the story projecting a general feeling of recovery and success.
3) Fund a subtle use of words used in mass media solidifying general populus belief (recovery, strong, trust, stable, taking risk, high profit) with a set of vague phrases hinting on recovery (reconstruction, rearrangement, restoration, resumption). Minimise potential consequences but make sure you mention them, so that one does not lose his credibility. The “we told you so” method.
3) Gradually in phases release large number of stocks causing sudden spikes down, and behave as if nothing happened. The “It’s the market, what can you do” method.
4) Rinse, wash and repeat.
\\\
This only works if all the links in the chain hold. So who will break ranks and when?
\\\
\\\
Sorry to bother with two comments on one article. But here is an observation from a process engineer whose job was to find tiny signals and process changes in a sea of technical problems.
\\\
I review economic indicator charts for the fun of it (yes, there are such people) and I noticed a change in the NASDAQ index today. It completely lost it’s dynamics…to be more specific, the rolling standard deviation of todays trading some 2 hours after start is significantly reduced. Or in plain terms – line before today was much noisy and random, and today …puffff…no noise, flat with minimum variation. I don’t get it.
\\\
The noise disappearing means that something has changed and Energy is being stored somewhere. The process is readying for a jump in hyperspace (many parameters change by a large value at once). Once the jump happens, the process will run towards another equilibrium and move around that. Like a creature (in hyperspace) fouraging around a lake (of stability, local optimum). In plasma physics, the plasma literally jumps and the energy release is dramatic.
Or One could say that the excursions follow a power law, meaning that the RMS-value of excursions over time is reasonably constant so to make up the average after a quiet period, a big excursion is needed.
Or the excursions are now happening in an internal / hidden property that we “flat-earthers” only looking at Price and Volume don’t observe.
I read it as a sign that something is up and a move is coming.
Nothing mystical – traders took off for the Thanksgiving Holiday
Typical engineering solution. In real life you want to unload a large holding you arrange a “”block trade” with other strong hands. They do report these things, so you want the trade to go off at the traded price, and if there is some asymmetry you arrange a quid pro quo. There are incentives for holding a hot potato (gloves).
WR; maybe you would like (or not) to weigh in on the pressure being put on the Fed to back off the return to normal rates and the unwind of QE.
Jim Cramer is injecting a new note of panic saying: ‘You’ll wish you’d sold at these prices if the Fed hikes in December’
Now the heat is coming from the Left too, with Elizabeth Warren chiming in saying (approx) that the Fed ‘misread subprime mortgages before 2008’
She doesn’t seem to grasp the irony in complaining about a problem caused by overly lose credit.
And of course the Commander in Chief has accused the Fed of ‘going crazy’
The tune from the band wagon seems to be: ‘thanks to the lowest real rates in a century, we’ve taken on so much debt you CAN”T normalize on us now!’
nick kelly,
Your last sentence is a great summary of the mood out there.
Stocks are flat for the year. That’s not a crash! Spreads are widening but are still too tight. The financial stress indices are all still in loosey-goosey territory. Etc. So for now, until this changes, the Fed is going to brush off Trump, Cramer, et al.
That said, I do think that neutral is around 3% federal funds rate, and that just a little over neutral would be about right with the current economy and current inflation, so maybe 3.0% to 3.5%. Many people whose primary concern is not asset prices see that too, as do many Fed heads. So I think the Fed will go to 3% and perhaps take one or two steps higher at the most, and then stop and look around. And I think that makes sense.
Monetary policy only becomes effective when markets react to it. The markets are finally reacting to monetary policy like they’re supposed to, after three years of ignoring it. This phenomenon is well documented and is called the “lag” in the “transmission channel.” But this three-year lag is a lot longer than the normal lag of 6-18 months – perhaps because the rate hikes were so “gradual.”
In terms of Senator Warren: I get the impression that she wants to be in every discussion in the US on every topic, to get her name out and position herself properly for the coming primary. That’s how I see her comments – and she’s now commenting on everything. I think the Fed sees this too.
RE: Warren, I strongly disagree. You may disagree with her priorities and policy solutions, but some fraction of her liberal base, myself included, strongly agree with her diagnosis and solutions. Her comments aren’t showboating they are core constituent concerns, namely
– Addressing a housing shortage that has enormous social and economic costs, significant enough, for example to turn a prosperous state with a rapidly growing economy into one with the highest poverty int he US That’s a higher poverty than states like West Virginia and Mississippi. And it’s entirely due to dysfunctional housing. Nationally, the housing shortage in major economic centers, has cost the economy up to $2 Trillion annually in lost productivity. You might argue the accuracy of those statistics but they are supported by reputable studies and statistics produced by various federal agencies. If they are correct you would be hard put to come up with any other issue that’s even close in magnitude.
Warren’s solution, stimulating market rate production, is only realistic solution and among progressives she’s alone in emphasizing it.
– With respect to Corporate debt, many believe, myself strongly, that a major amplifying factor if not outright cause of the 2008 financial meltdown was that mortgage securitization became too complex for the risk calculations made against various tranches to have any relation to the real underlying risk. What we’re seeing today is a new wave of such securitizations for corporate loans.. I believe that to be a far greater threat to the overall economy than the quantity of corporate debt or the interrelation of corporate debt, stock and Fed monetary policy. That’s certainly a minority position, but the argument is plausible enough that surely it can’t be dismissed outright, Warren’s making corporate debt reform a top priority is obviously consistent with that view.
Warren is an opportunist. Her use of her fake heritage is a prime example.
I should have deleted my last paragraph (Warren). I knew someone would take it wrong. I wasn’t saying that I disagreed with everything she said. I was saying that the Fed isn’t going to be pushed around by what she said.
“Addressing a housing shortage that has enormous social and economic costs” — mainly true in the NE and West coasts, so it is THEIR local problem to solve, and not a US problem. The solution is certainly NOT to have the affordable parts of the country subsidize the unaffordable parts. This should not be a part of any debate at the Federal level, just like CT should never be allowed to make their state pension crisis a national problem, as they want to do.
Hi Earl d. My oversimplification of the 2008 crash is this: The US government pushed the banks from ~1987 onwards into lending too much too cheaply in a housing market they should never have gotten into. One in there, they knew the risks would be moved onto the taxpayer. A bigger problem was that the rest of the world did not expect the endemic fraud hilighted by the FBI in 2005.
Oh Lord. Where do I even begin with this.
If she was serious about standing up for the middle and working classes, she would tackle the root of our economic problems: the Wall Street-Federal Reserve Looting Syndicate and its systematic looting and asset-stripping of the proles. “Stimulating market production” isn’t the way to counter housing bubbles that have priced out the prudent and responsible – it was the Fed’s “quantitive easing” that lavished trillions in free gambling money on the Fed’s Wall Street cohorts so they could speculate with reckless abandon, creating the Everything Bubble in the process. But Elizabeth Warren will never, ever call out the Fed for its “No Billionaire Left Behind” monetary policies and swindles against the 99%.
I really wonder about monetary policy, it might have been more logical for Yellen to have raised rates more back in 2014, to cool things off. It may not have inflated the everything bubble by quite so much. I am really curious on why the Feds decided four raises had to be done this year.
You can start to see things coming apart at the edges already, but the Feds didn’t seem to really signal a slow down. Because by your logic on the lag, markets are reacting to rates that’s in the 1.5% to 2% range now, or sub 1.5% depending on the lag. Then, in another eighteen months, people will really be panicking about the fact that today’s rates are between 2 to 2.25 percent.
I’m wondering if what you’re really saying is that the worst is yet to come as people come to terms with today’s rates
“Stocks are flat for the year.”
So nothing of significance has happened to the markets till now.
“So I think the Fed will go to 3% and perhaps take one or two steps higher at the most, and then stop and look around. And I think that makes sense.”
If this is treated as market swoon by the cry-babies at Wall Street (not to mention Trump, Cramer et all), what do you think we can expect on the markets by the time the Fed gets to 3%
Back when she was Chair if the Congressional Oversight Panel charged with reviewing the TARP program I found that she made a lot of sense, was very critical of Treasury’s use of the funds (particularly regarding GMAC) and was warning about how the actions being taken would have longer term negative impacts. I wonder what happened to that Elizabeth Warren…
Long term (pun intended) I think QT is more important the Fed Funds rate. That is the basis of the wild amount of liquidity that has be available. As that liquidity continues to go, you will get a bear steepener eventually. That will kill housing, longer term loans and bonds. Also the EU inflation rate is creeping up so the ECB is going to be getting pressure to keep to the plan of shutting down the spigot. Keep in mind unlike the Fed the ECB has a single prime objective, maintain price stability. Everything else is secondary.
Begging WR’s indulgence for a second comment. People like Cramer and their ilk saying the Fed should not stay the course are insane. The only way we have long rates so low is the complete confidence that the Fed will not allow inflation to get out of control. If the Fed suddenly changes course without serious economic (not stock market) guidance to fall back on there will be a crisis of confidence at the long end. This will cause the sighting of the “Bond Vigilante”, a species thought long extinct.
I would love to know how much individuals have
in margin vs companies, hedge funds etc.
Household Credit is at all time high and worse than 08. Non-performing Credit Card Loans are above 10% with defaults trending upwards all the time. Mortgage Debt & Credit Card Debt get rolled into incrementally worse deals and Non-Bank Lenders are issuing greater amounts of cov lite loans. The Hedgies are blowing up now and the Non-Banks will follow suit soon.
Companies have stock buyback whereas Joe Blow has merely more debt at higher rates and no new discretionary or disposable.
Joe Mainstreet USA can’t afford a crisis over $400.00 and Corporate America is awash in cash but no market to sell. The dominos will fall.
MOU
Companies have stock buyback whereas Joe Blow has merely more debt at higher rates and no new discretionary or disposable.
It used to be illegal for companies to buy back their own stock using borrowed money – for good reason, as we’re about to find out. The emphasis on “shareholder value” rather than promoting the long-term soundness of companies is resulting in looted shells of formerly solid and successful companies.
A more accurate term may be “Cheap Debt Bubble” and that explains why stuff like this is happening. Since cheap debt, while it still exists, is becoming a thing of the past.
Now that the cheap debt inflated values are forced to face reality, is sink, float or swim.
One bubble check I like to do is to value the sp500 dividends using dividend discount online calculator since it takes out single stock risk and sp500 is roughly 80% of us economy. Current div last i checked $52. Long term future nom growth rate about 5%. You can choose discount rate but using any rational number I can come up with you get sp500 value of 1000 – 1800. Using margin to buy a single stock in this elevated market is risky business.
Hi Wolf-
I’m sitting here boggling at your final long-timeframe margin debt figure, and wondering if the dollar values are inflation adjusted? I know you usually do, but man, that’s something else if so.
Nothing in these figures is inflation adjusted. The stock market itself is a measure of inflation: asset price inflation. Consumer price inflation (CPI, etc.) is irrelevant for asset price inflation (stocks) and the near-parallel margin debt.
The important part is not the absolute height of margin debt at each peak, but how ballooning margin debt accelerates the run-up of stock prices and the subsequent sell-off.
Thanks for the explanation Wolf, it makes sense.
In case of a broker bankruptsy, the common fate of risk-aversive and risk-prone clients is a form of “SBL” itself.
Wolf, here is an idea for your next article. How do you find out an estimate of the hidden debt in a company?
Because really, that’s a skill that a must have in the Smoke and Mirrors market of today.
Thinking about it, maybe is not a bad idea to legally threat companies as a person, because that means companies will be affected by laws that affect persons and so they won’t be able to get away with so much scams. If it quacks like a duck, flies like a duck and swims like a duck, then it can be hunted like a duck!
Really, all these new regulations seem to be targeted to make sure Big Tech pays their taxes and that they do paid more taxes, and thry respect privacy laws.
But what they are not doing is targetic stuff that should be illegal like LBOs, being more harsh in cases were companies hidde debt and so on.
You may think it may be like harding cats but I say is time those cats get snipped and get their shots.
How is it people can gamble it all on margin and sleep? It means counting on everyone else being an idiot as well. It’s like the ATM at the casino, irresistible.
Oh, you can sleep just fine as long as stocks go up :-]
First off, Happy Thanksgiving to everyone. I read the article and comments. My take, I’m a chartist, I saw this coming for the last six months and positioned my funds accordingly. I’ve been actually making money. I’ve learned I don’t care what works for others, I’m self taught and have taken my licks over the years. I read what others have to say and ponder it but i try to keep it simple and use indicators that I understand and that jive with the way my brain works and that fit my personality (wary, conservative, always looking for the risks). I was a little offended and defensive with what some on this thread said about boomers but to each his own. I don’t believe in all this generational bashing, every generation has its ups and downs. Finally, I grew up a surfer, it always amazed me that a hurricane somewhere is tearing up the sea lanes sinking boats, causing mayhem on shore and causing millions in damage; however, on the other side of the ocean surfers are skipping work, lying to wives and doing everything possible to get the the beach, hooting and hollering in anticipation of a new “epic” swell. Or as my dad used to say, one man’s trash is another man’s treasure. I’ve been waiting for this downtown for some time and hope, yes only hope, to make some money. I don’t surf any more but I swim in the ocean 3x a week year round. Blessings to all…
Joe, the weekly chart for /NG was much like Oil at 32, I made a killing on the this move, the widow maker is alive and one more spike is coming…..
what you say rings true for myself too, a surfer has millions of shores to surf. Look for the good waves even in ugly markets and you will succeed…
What is really happening is young day traders who have no idea what a weekly chart is are getting abused…..monthly too….trying to get rich quick in any market is death to your account. Waiting for opportunities is the key. No one can time things perfectly…..
Hey Joe
You’ve got your priorities right!
Knowing where to put your money in today’s market is more important than being in the market. Risk is alright if you know how to control it.
Stocks are not overvalued right now, 15PE is not a bubble…..tax loss selling, margin issues mentioned in this article, Forward PE being hit by some earnings expectation withdrawal etc…then add Brexit, Kashoggi killing and general unrest and a correction happens. It needed it….
the main target in all of this is the Chinese market, they have been milking us forever and now they are going to get their due thanks to the financial engineers…..
Tons of symbols are on sale if you are looking for growth or yield
You go ahead and load up on stocks, then. We’ll see how well that works out for you. Myself, I decline to buy into these Ponzi markets that are doomed to implode under the weight of their own fraud and mark-to-fantasy valuations. True price discovery, after ten years of central bank QE, is going to be a bitch.
Your US-centric posture has not served you well, and it will continue to sabatoge your wealth. Global capital flows swamp QE, buy backs, and other “manipulations”. How did the propaganda about dollar devalation work for you? Probably about as good as all the foreign entities that bought the same BS and loaded up on dollar-based debt.
Do you consider global capital flows, or are you US-centric?
What market and currency still has RELATIVE strength?
What is safer – govt bonds backed by nothing and at 5000-yr lows, or stocks with actual collateral?
When the govt bond bubble pops, what is the only market big enough to absorb the flows?
I don’t understand how you can say that the money repaid to a broker in a margin call disappears into thin air.
The broker has it, to lend again or park in other less lucrative investments until loans on margin get popular again.
The broker always has money to lend. When customer A pays off that margin loan, it doesn’t add fire power to anything the broker does because the broker already has all the firepower needed. That money just disappears from the market. If customer B wants a margin loan from the broker, he could have gotten it without customer A first paying off his margin loan. It’s called deleveraging. It crushes asset prices.