Repos at $0. SPVs fell for sixth week. Dollar liquidity swaps fell for 9th week. MBS unchanged for 3rd week. Treasuries rose.
By Wolf Richter for WOLF STREET.
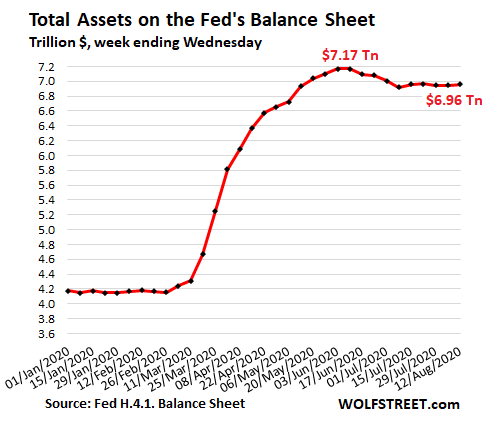
Total assets on the Fed’s balance sheet for the week ended August 12, released this afternoon, ticked up by $12 billion, to $6.96 trillion after two weeks in a row of declines, and are down by $212 billion since peak-QE on June 10.
Of that $12 billion increase, $4 billion was related to the Fed’s other activities and $8 billion was related to the five QE asset categories (rounded to nearest billion):
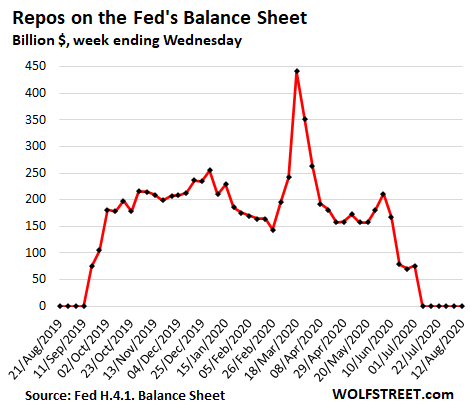
- Repos: no change, at $0 for sixth week in a row.
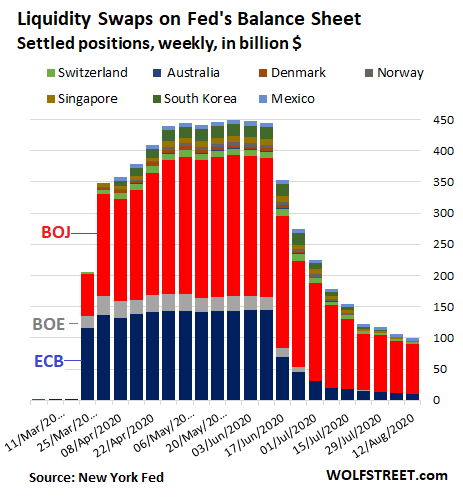
- Swaps: -$6 billion, down for ninth week in a row.
- SPVs: -$1 billion, down for sixth week in a row.
- MBS: no change, for third week in a row
- Treasury securities: +$14 billion
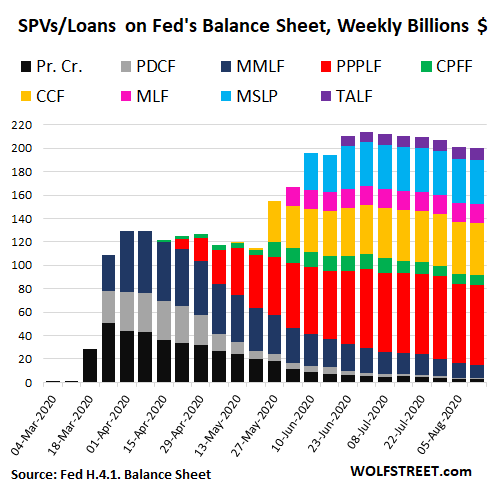
SPVs fell by $1 billion, 6th week in a row of declines.
The Fed conducts many of its QE operations via Special Purpose Vehicles (SPVs). These are LLCs that the Fed created and that it lends to, and that then use these funds, along with the equity capital provided by the Treasury Department, to buy assets and lend. This is the current alphabet soup of SPVs on the Fed’s balance sheet:
- PDCF: Primary Dealer Credit Facility
- MMLF: Money Market Mutual Fund Liquidity Facility
- PPPLF: Paycheck Protection Program Liquidity Facility
- CPFF: Commercial Paper Funding Facility
- CCF: Corporate Credit Facilities: Buy corporate bonds, bond ETFs, and corporate loans.
- MSLP: Main Street Lending Program
- MLF: Municipal Liquidity Facility
- TALF: Term Asset-Backed Securities Loan Facility
The SPVs’ combined balance ticked down by $1 billion from the prior week, to $200 billion, the lowest since June 17. The largest SPV currently is the PPP loan facility (red), with which the Fed buys PPP loans from banks. Note that the early SPVs are being phased out, and replaced by newer ones:
But wait…
The SPV “CCF” (yellow) is where the Fed holds its ballyhooed corporate bonds and bond-ETFs that it purchased. The current balance of the CCF is $44 billion. The Fed disclosed a few days ago what exactly is in it as of the end of July, including names of companies and ETFs and amounts.
This balance of $44 billion was composed of just $12 billion in corporate bonds and bond ETFs. That’s all the corporate bonds and ETFs the Fed has ever bought. The rest of the $44 billion was unused equity capital from the Treasury Department. Just $12 billion in bonds and ETFs… that’s all! Here’s my detailed analysis.
Repurchase Agreements (Repos) at zero, sixth week in a row.
Central-bank liquidity-swaps dropped by $6 billion.
The Fed’s “dollar liquidity swap lines,” designed to provide dollars to certain other central banks, are being phased out and have now dropped below $100 billion ($99.78 billion). The Bank of Japan is the big exception, accounting for $80 billion, or 80% of the total. Swaps with the ECB are down to $9 billion, with Mexico down to $5 billion, with Switzerland down to $3 billion, and with Singapore down to $2 billion. Swaps with the rest of the central banks have matured and are gone:
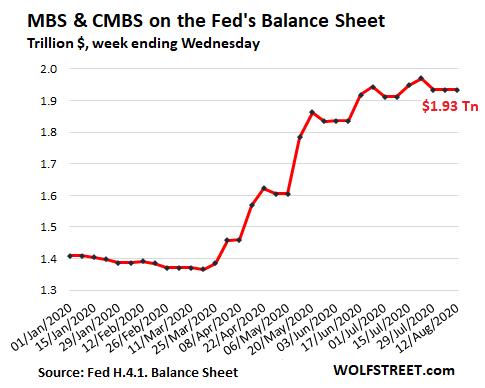
MBS unchanged, for third week at $1.93 trillion.
The balance of mortgage-backed securities remained unchanged at $1.93 trillion. These balances are erratic due to the pass-through principal payments, which are triggered when mortgages are paid off, such as during the current refinance boom; and due to the long settlement times of 1-3 months for these trades, and the Fed only books the trades after they settle:
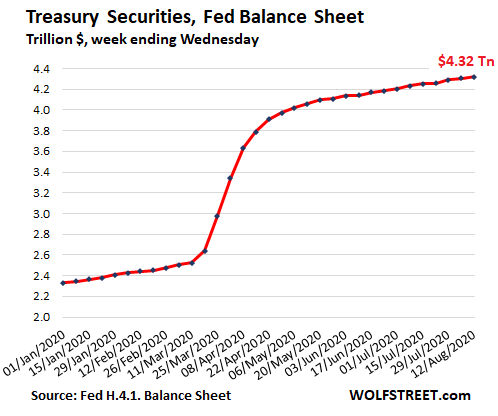
Treasury securities rose by $14 billion to $4.32 trillion.
Here are the details of the Fed’s purchases and holdings of corporate bonds and bond ETF, including names of ETFs and amounts. Read… Corporate Bond & Junk Bond Markets Driven into Foaming-at-the-Mouth Exuberance by Fed Jawboning about Huge Purchases. But it Actually Bought Just Tiny Amounts
Enjoy reading WOLF STREET and want to support it? You can donate. I appreciate it immensely. Click on the mug to find out how:
![]()


The more I think of it, the more I am convinced the Fed is irrelevant the way it is structured. They can only loan money. And we will start dealing pretty soon with a solvency crisis for which the Fed can do nothing. Unless the congress changes her status so it can spend money then all bets are off. but I dont see that happening in the current environment.
Private banks wont lend money either given the risk averse times we are in.
The big reflation will come through government guaranties to the commercial banks I believe. Banks will lend and the government will guarantee the losses through various guarantee schemes.
Indirectly the government will take over from the CB the control of money supply. It is already happening in Europe and its an irresistible proposal for the politicians.
Only congress may be less willing to monetize directly, for partisan reasons. Much easier to spend on the cuff and let the next Congress pass a debt ceiling bill. This could put the brakes on spending.
Next they are going to forgive student loans, in one fashion or another. No matter who wins.
Once they started negotiating in Trillions the student debt is as good as gone.
So when they forgive the student loans, do I get back the 5 years of full payments I’ve been making?
(We both know the answer to that question.)
Do I get back the 10 years of tuition I paid – without loans – for my kids college educations? Or will it be refunded to them?
(Yeah, we know the answer to those questions as well.)
Well I paid mine off years and years ago when the real value of the US$ was much higher.
Do I get a refund of the current inflation adjusted value of those dollars?
If student loans are “forgiven” will my pension fund remain solvent?
Lisa, it’s not inconceivable Venezuelan pension funds are still solvent.
“Next they are going to forgive student loans,”
Nothing is sure, but I wouldn’t be surprised by comeback of the good ole formulae “Join the Army to pay the College”.
Well one of the small benefits of joining the military way back when was that my lender stopped all interest on the loans for the time I was in the military.
Back then loan balances were much smaller and rates weren’t thatbad, but I guess every little bit helped.
And about a year after I got out of the military I wrote a check and paid off the entire amount.
It’s interesting too. Normally a forgiven debt counts as income if I remember correctly is classified as income, unless Congress makes a special provision to wave taxes.
“They can only loan money. And we will start dealing pretty soon with a solvency crisis for which the Fed can do nothing. ”
The Fed still can do :
1. Loans to maintain liquidity.
2. Not increasing the interest rates.
That is already huge, but not enough.
As mentioned by others, the gouvernment can garantee the new loans to tweak the notion of solvency.
That’ll give us several more years.
The Solution is yet to find… before it finds us.
Fed cannot buy all Treasury issues (old spending) and fund all of Congress stimulus (new spending). In the past they always sought to get the deficit under control, that is not an option. Fed went into the market and bought Treasuries at the onset. This is the point Drunkenmiller makes, after building reserves Fed must make room for an additional amount in new issues. The current balance sheet is enough to keep America in beans for a while. So who buys the new issues? Not the Fed. Let interest rates rise and Treasury can sell their paper. Higher yields help the banks and save the dollar. The stock market reacts after the election, that is the plan, and always when they plan to dump the market they pump it much higher first. However the economic news next year will start to improve and offset that bias in selling. Yield are going to rise, and best to let them out now, while the real economic pressure is very low.
Momento mori said: “They can only loan money.”
______________________________________
A bit of an understatement. They can create money, and they do. Far better for them to create the money they loan. They get to earn interest on the money they create.
If you think about it there are real goods and services and there is real capital stock of factories, infrastructure and the like. Its obvious that in the very short term the Fed can’t do anything with the real stuff and over the very long term it doesnt look like they are helping the real economy either as growth rates keep grinding lower.
My take is since they were created by Congress, their main function is to benefit politicians and those that contribute to them. Just look at it the last few months as politicians can hand out 2 or 3 trillion in an election year.
The sad thing is the more you know about the complex system, the more you can benefit from it. How many of us would have done something different if we knew the Fed was going to blow up the balance sheet to $7 trillion.
I still think they might have a fatal error in trying to a hit 2% inflation. If what you are doing has a feedback loop that doesn’t generate inflation due to demographics or tech innovation are you just going to keep running more extreme policy like Japan?
The FED was created to benefit themselves (the owners of the FED). They manipulated Congress, and Woodrow Wilson into supporting them.
It’s got to change. Last 10 years has been the great asset inflation. Just looked at chart on vanguard balanced fund. Right at 10% per year up and to the right with hardly a wiggle. That should have allowed pension funds to get their house in order but the promises we’re so big. How can it not be a rough decade coming up.
The market mostly stalled since about first week of July. Kinda like Feds balance sheet. Momemtum stocks lost all momemtum and trading in range. Just one good push and it’s gonna keel over.
SPY up 6% from early July is “stalled” only with respect to insane +/- 5%, even +/- 10% days we saw in March.
That’s something like a 60+% annualized return.
Markets deteriorate underneath before index will show it. I watch composition. Leading issues stalled in sequence since about first week of july. Some were making new highs as recent as this and last week. Maybe another 3 weeks of this.
Keep indexing and watch the keel over part.
Thanks for that. You sound like you know what your talking about, and To me there are a lot of reasons I see about 3 weeks before the market and gold get a beat down. Not sure where shares go after, but I think back up with gold. I can’t see this slowing down now The money will keep flowing.
Though, I see the dollar collapsing.
Nothing like a Pandemic to pull the wool over our eyes.
So who will be buying Treasuries at current real yields over (-1%) with deficits for next year projected to be 5-6 trillion.
Those that expect rates to fall even further.
Those who buy it on leverage and use it as collateral to keep their insolvent positions open… lol
Anybody who doesn’t trust their own currency is buying treasuries. It’s another way to get money out.
Or gold
US Gov spending can only accelerate so Fed UST buying must increase. US negative rates will be necessary to finance it regardless of what the Fed see’s or wishes.
If you believe Gold rises against increasingly negative real rates then we’re in for a long bull market in it and Silver. I’m adding to my Gold miner ETF’s on pullbacks below $1880/oz but budgeting to buy down to $1650/oz. When DXY falls below 88 the Fed + banks will be pulling out the monkey hammer so I’m anticipating some last chance bargains. I’m only shedding small portions when I see %100 profits but feel even that’s ‘giving away’ shares.
Investors are ignoring the fact that in just the last year hyperinflation has moved up the ladder from Zimbabwe and Venezuela into Argentina, Turkey, Brazil and Iran. India, Mexico, Canada and Hong Kong are next on the menu. Once that live wire touches the Yen or Yuan, currency hedges and swaps will implode. Ever seen USDJPY spike from 107 to 140 overnight? You might just. EU and US markets/banks will not escape and I see $10 trillion stimlous amidst a historic spike in DXY followed by the biggest/fastest drop in history. After that, everything looks like a hockey stick.
If you’re expecting another massive spike in DXY, then why buy gold before then? Rising dollar crushes everything, including PM’s.
I share your thesis btw.
And who is buying them now ? Massive spending and massive auctions….and the data doesnt show the Fed increasing their Treasury holdings to any degree..
I think the Fed has learned a trick, an off the books tactic ….
Repos drop that much?
Didnt see any discount window activity numbers..
Fed buys Apple bonds…??
SNB owns tons of Apple stock…
what hand is washing the other hand?
Wolf,
Second chart as highlighted has MLF ( pink & blue) twice & no MLSP or just me confused?
Oops. Thanks.
“…along with the equity capital provided by the Treasury Department, to buy assets and lend.”
Equity capital from the Treasury…which is BORROWED!
I’m old enough to remember when $1T was a lot of money.
I’m old enough to remember when a million ($) was!
And I thought if I ever made $25K per year as an engineer, I was set for life……ugh.
Certainly dating myself here!
Yup. The hope was to save a million and live out retirement on $50k/year interest. A safe million now yields about $5k/year which doesn’t cover property taxes. Didn’t work out as planned.
One million divided by 50k = 20 years of retirement at 50k.
What, you think you’re going to live forever ?
Not exactly sure that this is the right way to think about it, but plugging it into a discount calculator at 1/2% interest and 2% inflation I get a million is net present value is a little over $200,000. Whether it’s exactly right it shows the amount of damage negative real rates do and why government loves them so much for solving debt problems.
Ah yes the net present value and inflation argument !
Amazing how this only shows up when discussing retirement/investments but never shows up when discussing salaries and compensation.
After all retirement ( for most folks ) is a small slice of life….or for many not at all.
The bulk of life is spent working.
Lisa_Hooker,
A Walmart greeter, if they still existed, would make more money off his work than off $1 million in Treasuries, Apple bonds, or CDs.
In Europe, an Aldi greeter, if they existed, would make more off his job than the interest off $1 trillion in German government 10-year bonds.
This world is really screwed up.
The only fed chart that matters right now it the treasury general account. Take a look, very instructive.
Wow that’s heuge – and it’s never happened before even in 08. What is going on?
The Treasury needs to raise cash in advance to be able to pay for all the money spoken for under the CARES Act… $3 trillion to be spent over the next few months or so… so it has to borrow this cash in advance so it won’t run out when it comes time to pay. The Treasury is paying out huge amounts of money to consumers, companies, and states, under all the stimulus programs, and this will continue for months, and it needs to have this cash ready to do. That’s all.
And the Fed is the bank of the Treasury Dept., and so the Treasury Dept. puts its cash on deposit at the Fed, like I put my cash on deposit at my bank. But the amounts are a little different. This deposit is a liability on the Fed’s balance sheet, not an asset.
So this surging deposit at the Fed was expected, and it makes total sense.
Wolf said: ” This deposit is a liability on the Fed’s balance sheet, not an asset.”
___________________________
So if the Treasury puts its cash on deposit at the FED, resulting in a liability on the FED’s balance sheet, what is the offsetting asset on the FED’s balance sheet?
Basically the Fed is the monetary base. The two charts correlate, even the recent pullback. No surprise with economic activity stalled. Everything pivots on the dollar, and the implied collateral value of the securities on the Feds balance sheet. Should the Fed balance sheet be impaired, or for political reasons the Fed is instructed to pare down the balance sheet, which is a conduit to Congressional spending, the fabric of the social safety net collapses.
People really do not understand the implications of the moral hazard being created by the FED. People have the mistaken impression that supplying money is the answer to the problem, instead of the cause of it.
The fact is that money is simply a way to keep score of productivity. At the point where you produce money without corresponding productivity the incentive to be productive goes out the window. When you pay people not to work, they will not work. When you loan money to companies for practically free, they have less incentive to innovate and be productive.
All of this is counterproductive and incentivizes the wrong behaviors.
Our prosperity depends on productivity, and everything the FED and the government does de-incentivizes work and production. It is just a matter of time before that completely ruins the economy.
Printing money has also made getting elected easier. Legislators no longer have to be productive.
But the biggest winner is the C-Suite. They can keep the gravy train flowing by simply laying off employees and buying back stock. You get paid hundreds of millions to shrink a company. What talent or expertise is required for that?
With you 100% on your main themes in your post jdog,,, Good one!!
When the time comes, once again the folks with their PMs in canning jars in the yard will be fine, while all the rest of We the Peedons will be lining up at the soup kitchens if there is even enough guv mint and NGOs and so forth still standing… if not,,, I suppose we will see again some semblance of what has occurred during and after various extreme wars in the world since for eva,,,
I certainly hope USA and the entire world does not come to that place; but, if these financial idiots who think they can extend and pretend for eva,,, along with the now well recognized covidiots who think they will never get it, the virus it, though certainly they have not got the other it, common sense and the third it, community spirit, so will be a constant and continuing drag on the rest of humanity, don’t find a way back to a fair and level financial and social world where honest labor and production are valued correctly, we are doomed to rinse and repeat and rinse and threepeat, etc., for eva, with the crony and corrupt continuing to manipulate and steal until death do us part.
Thanking the Great Spirits that I will not be here, at least in this tired old body, to have to deal with this kind of shyte, though feel sorry for the boomers and other youngsters who will have to do so…
And then you have another May,1789
Yep. DEflation is the natural state of a productive economy. Bankers and bureaucrats can’t survive in this state, however, so they fight against it with the only weapon they have – money printing. Eventually it corrupts us all.
People have been duped into being debt slaves.
Everything the FED does incentivizes debt, since bankers are in the debt business.
The economy has been ruined for some time. How else would you describe an economy where savings and savers are punished.
There is nothing moral about the FED.
So let’s see…..savers built up a pile of money….so now they should be given more because they have a pile already ?
Talk about ENTITLED !
I suppose it might be viewed as entitled to expect money earned, and paid in paid in legal tender, to retain any purchasing power.
A question is: Should savers, particularly those savers who traded their labor for dollars, be subjected to the destruction of their savings by a group (FED/Bankers) who get to create dollars out of nothing and loan those dollars at interest?
If that is okay, the FED seems to have a good system for it.
In the real world, the people who have money, have usually earned it by being productive. Rewarding people for being productive increases prosperity, while rewarding them for being unproductive causes the collapse of society. We have seen this play out first hand in every society which has embraced socialism and communism.
Savers built the pile of money believing in a risk free rate of over 5-6%. Today the risk free rate is negative. The principles of investing have been erased. Instead we have to blindly follow the Fed and speculate or gamble on equities. Forget valuations or cash flow. This goes against everthing I ever learned and against basic logic. So yes I do feel entitled or bitter to be so badly let down. I also feel disappointed by the ignorance of the voting public. But that is another problem with no solution.
cb
Money is meant for spending.
Money in and of itself does not constitute an investment.
Then I suppose the question is where to invest ones money. There was a time, certificates of deposit (savings) would yield 5 or 6%. This was where many “prudent” working people, who were lucky enough to get a few dollars ahead and that recognized their limits of financial sophistication, would put their savings.
This hasn’t worked out too well for them. Some think the FED has a role in this (suppressed interest rates, money printing and inflation).
How would you recommend those people invest their dollars?
cb
Take that pile of money and buy rental property.
You have used the pile of money for its intended use: spending.
And you have obtained a profitable investment that is inflation resistant.
Interesting move by fannie adding a 50bps hike on refi costs, not rates, for loans closing September 1 on.
That is one way to motivate people to get that Re-Refi sooner rather than later. Many of my owner friends refinanced their 30 year mortgage this year. It has become a competition for the lowest rate. My motivation is to have a mortgage burning party as my mother said to me a long time ago. Happy with my almost paid of 2.875% 15 year
It really is a wonder full feeling to burn the last mortgage ND,
Wish we had done it earlier, rather than playing games with the refi cash to invest, although that did pay some good dividends in the short run…
Best of luck going forward with only taxes, utilities, and maintenance, usually a small fraction of the total with a mortgage.
RESIST that urge to refi and invest with the cash, not matter how convincing the propaganda from all sides becomes!!
Always refi at a better rate and lower payment for the same term, if no cost to refi, and then take those monthly savings and use them to pay down principal.
PDCF: Primary Dealer Credit Facility
MMLF: Money Market Mutual Fund Liquidity Facility
PPPLF: Paycheck Protection Program Liquidity Facility
CPFF: Commercial Paper Funding Facility
CCF: Corporate Credit Facilities: Buy corporate bonds, bond ETFs, and corporate loans.
MSLP: Main Street Lending Program
MLF: Municipal Liquidity Facility
TALF: Term Asset-Backed Securities Loan Facility
Is this the same number of levers the Wizard of Oz had behind the curtain?
This will not end well.
The biggie is the SPV to buy municipal debt. Will the Fed allow the democrat managed and bankrupted states and municipalities to die. Is the Fed the arbiter of political position, i.e., riots?
Ain’t my problem bro. I was supposed to die a long time ago.
The Fed has long decided which companies get to live, and which get to die. And it has decided to hit workers with inflation, gutting the purchasing power of the lower 50% on the income scale. It has decided to bail out billionaires and millionaires. No problem, OK? Texas and its municipalities are in deep trouble, as are its counterparts on the left and right coasts. They’re all clamoring for money.
Cue the Hank Williams music. Camera pans down main street of Anarene and stops at cinema where last picture show has closed following “Red River” (fitting name for what flowed from China). Don’t expect to get the mail delivered anytime soon. No one remembers how to tackle the other team once in a while. It’s gonna be a losing season. No point in sweeping the intersection.
Breaking News: Buffet’s latest 13-F shows that he’s dumped Goldman and he’s bought 20.5 million shares of Barrick Gold.
Buffet’s famous speech: “(Gold) gets dug out of the ground in Africa, or someplace. Then we melt it down, dig another hole, bury it again and pay people to stand around guarding it. It has no utility. Anyone watching from Mars would be scratching their head.”
Our hypocritical American “capitalist” (is there any other kind) just made a 180 degree turn.
Come join Buffet as he bets against the US Dollar!!!
Saw that and had a nice chuckle myself. How times have changed. He did two things right this year. Dumping airlines after buying the dip and this.
He was sucker punched on the airlines, but it was an investment that went against his methods. More proof there is too much money chasing too few investments. He then made BofA his second largest position?? As long as the Fed can draw a breath the first bailout money will go to them. This economy is not the same one where he made his stake. He likes to buy businesses, not stocks, and now the Fed props up the debt of every business. He should have doubled down on his airline investment and left those bank stocks alone. If you take away their stock trading profits they are in the same condition as the airlines.
This was probably a Weschler or Combs move. Not Buffett, and certainly not Munger.
They all are value type investors that try to estimate future income streams. My guess is it’s a play that current situation is good for gold which they see as any other product and that Barrick CEO is very competent and has improved the gold mining company. It’s the opposite of airlines where you have collapse in demand. You have increased demand and higher gross margins as gold price rises.
I’m not sure it’s hypocritical. He was making a statement during a very different time, when it wasn’t yet clear that the central banks would do all they could to destroy the value of the currency to prop up asset prices.
His comment would be correct in a free market. We don’t have that right now.
Buffet has always been a hypocrite. He didn’t believe in free markets. “Moat” = potential of becoming a monopoly. He too didn’t mind getting bailed out and receiving preferential treatments that others wouldn’t be able to get.
Americans are so easy to fool.
I have been a shareholder before. He is very shareholder friendly CEO. He always keeps a ton of liquidity and says if the system implodes his company will be the last big company to go down the tubes.
I really don’t think he got bailed out except that the system locked up in the great financial crisis and the system was saved. He was not happy that the CEOs that caused the problem didn’t lose all their money. Most people don’t know that nearly all of his 90 companies are bought with cash and use no leverage after being purchased. (Unlike private equity which should be called private leveraged equity). There are a couple of big exceptions which are BNSF and the utility company, but they are still conservatively financed.
“I really don’t think he got bailed out except that the system locked up in the great financial crisis and the system was saved”
At his size, he was and is still a big part of the system.
As I said before, Americans are easy to fool, but that’s also because Americans are experts at fooling themselves. It must be nice going through life with one eye closed.
You basically can have a merit based system where people can turn $1.00 into more than $1.00 or a political based system where $1 is turned into less than $1. Of course the best outcome is a free market system with democracy putting in the right amount of safety nets and regs. We have strayed a bit from that, but it’s a work in progress.
Why is it that there can only be 2 possible choices in this country? Left or Right, Yes or No, etc? Why can’t there be a system where for some people $1 turns into $1 gazillion no matter what and for others it’s $1 turning to $0.
Hei look, it’s the system we have in the USA. We bailed out the bankers and Uncle Warren. As I said, it must be nice to be delusional. There’s systems that we can have and then there’s the system we actually have.
I’m fairly sure he got gold a few years ago… by the time people had heard and were celebrating he had sold it.
As everyone probably knows by now, people in Melbourne, Australia are in lockdown.
Lots of ‘interesting’ stuff going on here all the time.
Yesterday Commonwealth Bank, the biggest bank in Australia, had another one of its crashes and people couldn’t use their cards or Internet banking.
People that went shopping and didn’t have any cash……well guess what?
The bank’s customers couldn’t buy food, gasoline, or mail a package at the post office.
These crashes seem to be a regular happening with the banks in this country.
And another example of hoading was reported in the local left wing rag: people are hoading Australian $50 bills.
When I read the article, I had to go to the Reserve Bank of Australia (RBA) web to confirm some of the figures.
Australians socked away about $A6 billion in $A50 notes since February.
Okay, for those of you in the USA, and the reason I had to check the numbers out was that at the end of last year the total amount of currency in circulation in Australia was a total of A$80 billion.
Yep, A$80 billion. Compared to the USA that number is basically meaningless.
In one week from August 5 to August 12 the amount of currency in circulation in the USA went up by US$6.4 billion (A$8.8 billion).
That’s about 10% of the total in circulation in Australia.
The head of the RBA stated:
“Some people seem to be wanting to keep some extra money at home,”
Duh.
This is the same RBA that has done a perfect job of jawboning and nothing else. Their forecast about the Australian economy haven’t been anywhere near reality for the past three or four years. A monkey throwing darts could have done better.
And by the way the A$ is actually up against the US$ by about 2% since the start of theyear despite the problems we are having.
I have no idea why and IMO there is no logical reason for the A$ to be up against the US$.
Commodities!!!
Gives the song “Your Cheatin’ Heart” new meaning!
Oops! Meant to enter this after the comment about cueing up Hank Williams music.
Maybe a better one for the Fed is “Why don’t you love me like you used to do?”
Or “Hey, Good Lookin'”…….so “how’s about cookin’ somethin’ up with me”.
Study the money flow, as the Fed follows the political “free money” gravey train on the fiscal side. On the monetary side, the Fed actually follows Wall Street wishes in order to stop the tantrums from tipping the artificial market house-of-cards. Yes the Fed pushes the printing press button, but the political system and Wall Street force the Fed’s hand weekly. And thus that is why on a weekly basis, the markets are up 66% of the time in 2020, during the worse recession year in the last 80 years!?!? Ironically, the market has rised 69% of the time over the last 120 years so just another “average” year for Wall Street, not so much for Main Street but we can dream of more main street free money, right??? What is not average is both sides in Washington are constantly begging the Fed to print trillions more to buy votes in the name of mercy. Trillion is now the new billion in both Washington and Wall Street, yet duly note that if you spend $1 million a day, it takes 2739.7 years to spend $1 Trillion!!!
If you want proof that the Fed follows the politicians, see the Bloomberg quote from last Thursday below:
“Our best shot with them is to say ‘all you care about, in our view, is the stock market,’” House Speaker Nancy Pelosi said on MSNBC Thursday. “Why can’t we spend some more trillions of dollars to shore up America’s working families?”
And so as the politicians diddle daddle until the end of September on whether we print another $1.5 or $3.4 Trillion on the fourth “buy votes” package this year alone, and Wall Street finally punishes the Fed by forcing the market down to a “Scary” SP500 level of 3,000 (20 forward P/E), then what else can the fed do besides printing trillions for BOTH Wall Street and the Main Street political system. The Fed’s hand is being forced and WE are all to blame as I do not see anyone marching in Washington because their 401k is artificially inflated 50% currently, or they are getting $1000/week to not work a $500/week job. WE ARE TO BLAME AS A SOCIETY, the Fed is only the tool WE use and thus BLAME in order to systematically destroy democracy and capitalism at an ever accelerating pace…
The Fed is trying to pump and dump, but they are not very good at it….